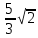х - = 0

10х + 20 + 5 х- 5 = 0

5x*(2+ = 5 – 20

x = 3 – 5

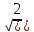y = - * (3 – 5) +

y = 5 -

Таким образом, биссектриса АС₃ пересекает сторону ВС в точке С₃ (3 – 5;5 - ).

Найдем длину биссектрисы АС₃, используя известные координаты точек А и С₃:

АС3 = 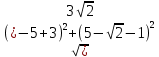= = 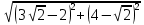= = 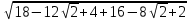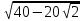2

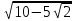
Найдем уравнения прямых, параллельных сторонам и проходящим через вершины треугольника:

Прямая, параллельная стороне АВ, проходит через точку С (1;3) и имеет угловой коэффициент k = 3, тогда находим коэффициент b:

3 = 3*1+b

b = 0

Уравнение прямой будет иметь вид у = 3х

Прямая, параллельная стороне АС, проходит через точку В (-2;4) и имеет угловой коэффициент k = , тогда находим коэффициент b:

4 = * (-2) + b

b = 5

Уравнение прямой будет иметь вид у = х + 5

Прямая, параллельная стороне ВС, проходит через точку А (-3;1) и имеет угловой коэффициент k =- , тогда находим коэффициент b:

1 = - * (-3) + b

---

b = 0

Уравнение прямой будет иметь вид у =- х

Ответ: у = 3x + 10; у = x + ; у = - x +

у = х + 4;

у = 3х + 10;

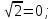3х – у + 10 + х - 2 у + 5 2

у = 3х; у = х + 5; у =- х

---

Раздел № 3. Аналитическая геометрия

Задача 2, вариант 6

1. 
   Найдем длину отрезка АВ, зная координаты точки А (0;2;-1) и точки В (-1;2;3):
   

= = = =

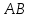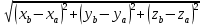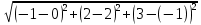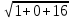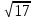
Найдем длину отрезка АС, зная координаты точки А (0;2;-1) и точки С (-2;3;-1):

= = = =

2. 
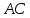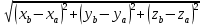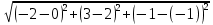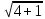   Найдем вектор 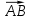по координатам точки А (0;2;-1) и точки В (-1;2;3):
   

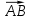= {Вх – Ах; Ву – Ау; Вz – Az} = {-1-0; 2-2; 3 – (-1)} = {-1;0;4}

Найдем вектор 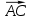по координатам точек А (0;2;-1) и С (-2;3;-1):

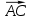= {Сх – Ах; Су – Ау; Сz – Az} = {-2-0; 3-2; -1 - (-1)} = {-2;1;0}

Найдем скалярное произведение векторов 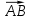и 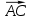по формуле:

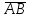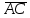* = АВ_х * АС_y* + АB_у * АC_у + АВ_z * AC_z = -1*(-2) + 0*1+4*0 = 2

Найдем угол между векторами:

cos BAC = = = ≈

---

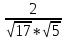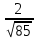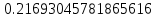
, значит угол ВАС ≈ 77.47119229084849°.

3. 
   Для нахождения площади треугольника АВС используем формулу:
   

S = |AB * AC|

Найдем векторное произведение векторов АВ и АС:

= *

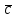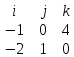* = = i * (0*0 – 1*4) – j * (-1*0 – (-2)*4 + k * (-1*1- (-2)*0) = -4i - 8j – k

={-4;-8;-1}.

Найдем длину (модуль) вектора :

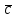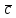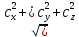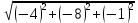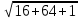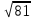| | = = = = = 9

S = * 9 = 4.5.

4. 
   Для нахождения проекции вектора на вектора применим формулу:
   

Пр_аb =

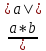
Скалярное произведение векторов а*b = 2, |a| = = =

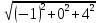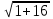Найдем длину (модуль) вектора |a|:

|a| = 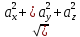= = 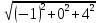, тогда

Пр_аb =

5. 
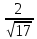
   Объем пирамиды можно найти по формуле:
   

V =

---

|

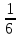
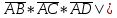
Найдем вектор 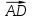по координатам точки А (0;2;-1) и точки D (0;4;1):

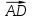= {Dх – Ах; Dу – Ау; Dz – Az} = {0-0; 4-2; 1 – (-1)} = {0;2;2}

Найдем произведение векторов 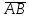, 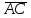и :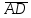

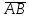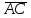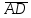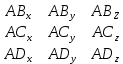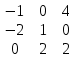* * = = = -1*1*2 + 0*0*0 + (-2)*4*2 – 0*1*4 – (-2)*0*2 – (-1)*2*0 = -2 – 16 = -18

Тогда объем пирамиды равен:

V = |-18 = 3

Ответ: 1) ;

2) 77.47119229084849°

3) 4.5

4)

5) 3

---

Смотрите также файлы

• Max пад. Рmin.docx

• Httppomogala ru.pdf

• Обычно понимается определяемое на основании коллизионной нормы право.docx

• Условный оператор Условный оператор.ppt

• 1. Понятие и виды унификации в международном частном праве. Унификация.docx