ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 30
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА МАТЕМАТИКИ
по дисциплине «Математика»
на тему: «Векторы в пространстве» для обучающихся 1 курса,
Дата проведения урока: Место проведения: Цели урока:
А. Учебные цели (для обучающихся):
1) формировать у обучающихся общие компетенции: ОК-1-7;
2) на основе понятия вектора в курсе планиметрии изучить векторы в пространстве, определить основные понятия для векторов: направление вектора, абсолютная величина, равенство векторов, нулевой вектор; закрепить новые понятия на практических задачах;
3) развивать качества мышления, умение наблюдать, обобщать, анализировать, совершенствовать пространственное воображение;
4) воспитывать математическую культуру, взаимопомощь, умение слушать товарища, чувство ответственности за коллектив в процессе творческой работы.
Б. Методические цели (для преподавателя):
1) формировать у обучающихся общие компетенции: ОК-1-7;
2) формировать представление о векторе в пространстве;
3) организовать самостоятельную работу учащихся;
4) учить сравнивать, обобщать, анализировать ответы товарищей.
Задачи урока:
А. Учебные задачи (для обучающихся):
1) сформировать умение применять формулы, определения;
2) развивать самостоятельность мышления, ответственность за выполненную работу;
3) воспитывать умение работать в команде, чувство ответственности за работу членов команды, за результат деятельности.
Б. Методические задачи (для преподавателя):
1) применить активные и интерактивные формы и методы обучения студентов для достижения образовательных результатов;
2) развивать умения обучающихся четко, кратко излагать свои мысли, делать выводы и обобщения, анализировать;
3) способствовать активному усвоению нового учебного материала студентами;
4) воспитывать интерес к учебной дисциплине «математика»,
5) формировать умение объективно оценивать свои знания (чужой ответ) и умение работать в группе;
5) формировать коммуникативную культуру, самостоятельность, способность войти в группу (коллектив) и внести свой вклад.
Тип урока: урок усвоения новых знаний.
Форма проведения урока: БИТ – беседа, игра и творчество.
Образовательные результаты урока, заявленные во ФГОС СПО:
-
Знания:
1) представление о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
2) представление о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления;
3) методы доказательств и алгоритмов решения.
-
Умения:
применять методы доказательств и алгоритмов решения, проводить доказательные рассуждения в ходе решения задач.
-
Общие компетенции:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.
Средства обучения:
1) мультимедийный проектор – 1 шт.;
2) экран – 1 шт.;
3) доска для написания маркерами – 1 шт.;
4) персональный компьютер – 1 шт.;
5) музыкальное сопровождение;
6) кластер на листе А4 – 3 шт.;
7) комплекс необходимого программного обеспечения;
8) Интернет ресурсы;
9) УМК – по количеству студентов;
10) таблица – 1 шт.;
11) карточки – задания – 3шт.;
12) пишущие и чертежные принадлежности – по количеству студентов;
13) карточки – домино – 9 шт.
Педагогические технологии, используемые на уроке:
- проблемного бучения;
- компьютерного обучения;
- алгоритмизированного обучения;
- дифференцированного обучения;
- развивающего обучения;
- проектного обучения;
- интерактивного обучения;
- модульного обучения;
- работы с опорной книгой (УМКД);
- эвристического обучения.
Методы обучения, реализуемые на уроке:
- проблемная лекция;
- метод иллюстрации;
- работа с УМК;
- метод микро-упражнений;
- метод ролевой игры;
- метод учебно-творческого самовыражения;
- метод сравнения;
- самоконтроль;
- метод анализа конкретных ситуаций;
- метод действия по алгоритму;
- метод игровых ситуаций;
- эвристическая беседа;
- метод проектов.
Дидактические принципы, реализуемые на уроке:
- принцип научности;
- принцип систематичности и последовательности;
- принцип связи теории с практикой;
- принцип доступности и посильности в обучении;
- принцип сознательности и активности в обучении;
- принцип прочности усвоения знаний, умений;
- принцип наглядности;
- принцип воспитания;
- принцип самоактуализации;
- принцип индивидуальности;
- принцип выбора;
-принцип творчества и успеха;
-принцип доверия и поддержки.
Приемы педагогической техники, используемые на уроке:
- работа с информацией;
- составление задания;
- использование системы наводящих вопросов в случаях неправильных ответов;
- групповое деление студентов;
- использование ассистентов;
- использование символов «внимание».
Подходы к обучению, реализуемые на уроке:
- компетентностный;
- психологический;
- рефлексивный;
- деятельностный;
- личностно-ориентированный;
- коммуникативный.
ПЛАН УРОКА
1. Организационный момент – 5 мин.
2. Актуализация опорных знаний – 5 мин.
3. Изучение нового материала – 40 мин.
4. Закрепление материала – 35 мин.
5. Итоги урока – 3 мин.
6. Домашнее задание – 2мин.
ХОД УРОКА
Группа разделена на три подгруппы. У каждой подгруппы имеется главный редактор, который контролировал создание газеты «Вектор, как много в этом слове». Газета состоит из статей «Немного истории», «Уголок программиста», «Векторы вокруг нас», «Математики о векторах», сказки, ребусов, кроссворда, гороскопа, рекламы и т.д.
1. Организационный момент.
Преподаватель. Здравствуйте, уважаемые студенты!
Проверка посещаемости.
Преподаватель. Ребята, сегодня у нас необычный урок. Мы проведём урок – бит. БИТ – это беседа, игра и творчество.
На уроке присутствуют гости: преподаватели колледжа, члены администрации, корреспонденты и кандидаты наук.
В основном на уроке будет групповая работа. Не забывайте, что групповая работа – сотрудничество, необходимо уметь слушать и слышать товарища. В конце занятия главные редакторы подведут итоги вашей работы.
Урок мы начнем с просмотра видеоролика.
Просмотр видеоролика (басня «Лебедь, рак и щука»).
Преподаватель. Итак, тема сегодняшнего урока «Векторы в пространстве». На вопрос басни мы сможем ответить на следующем занятии. А пока мы с вами должны вспомнить понятие вектора на плоскости, рассмотреть понятие вектора в пространстве и заполнить таблицу 1.
Таблица 1
Название определения
Формулировка определения
Запись
Вектор Нулевой вектор Коллинеарные векторы Сонаправленные Противоположно-направленныеКоординаты вектора
Абсолютная величина Равные векторы
2. Актуализация опорных знаний.
Преподаватель. Ребята, Вы знакомы с понятием вектора на плоскости и действиями над ними. Давайте вспомним, что мы называем вектором?
Для того, что повторить понятие вектора, мы заполним кластер. На листах А4 в центре имеется слово «вектор». Вам необходимо написать вокруг касающиеся этого слова понятия, определения, формулы, символы и т.д.
Студенты заполняют кластер.
К кластерам мы вернемся в конце занятия.
3. Изучение нового материала.
1. Беседа.
Преподаватель.
1. Что такое вектор? (Вектор – направленный отрезок)
Просмотр анимации.
2. С понятием «вектор» вам приходилось встречаться очень часто. Где?
Вам предлагается обсудить в группах и предоставить как можно больше фактов.
Мнения обучающихся.
2. Защита мини-проект «Векторы вокруг нас».
Преподаватель. Этим вопросом интересовался корреспондент журнала «Планета вокруг нас»… (ФИО обучающегося).
Защита проекта сопровождается презентацией. Вопросы обучающихся авторам проектов.
3. Примеры направлений движения (Просмотр анимаций).
4. Беседа.
Преподаватель.
1. Каким образом изображается вектор на рисунке?
(Стрелкой)
2. Обозначается? (Либо большими, либо прописными латинскими буквами).
5. Защита мини-проекта «История развития вектора».
Преподаватель. Кто же придумал понятие вектор? Более подробно, на этот вопрос нам ответит доктор исторических наук … (ФИО обучающегося).
Защита проекта сопровождается презентацией. Вопросы обучающихся авторам проектов.
6. Беседа.
Преподаватель. Мы с вами определили понятие вектора. Далее рассмотрим направление вектора, абсолютную величину, равенство векторов.
1. Как называется вектор, у которого начало совпадает с концом? (Нулевым, обозначение
2. Как называются ненулевые векторы, которые лежат на одной прямой или на параллельных прямых? (Коллинеарные)
Коллинеарные векторы – это ненулевые векторы, которые лежат на одной прямой или на параллельных прямых.
3. Итак, вектор – это направленный отрезок, а если у нас имеется два вектора, как могут быть направлены эти векторы? (Сонаправленными, противоположно-направленными, обозначаются стрелками)
Преподаватель. В пространстве два вектора могут быть одинаково-направленными и противоположно-направленными. Например, два проводника притягиваются, если электрический ток проходит в одном направлении; отталкиваются, если электрический ток проходит в противоположных направлениях.
4. Как определить координаты вектора, если известны координаты начала и конца? (Из координат конца вектора вычесть координаты начала)
Преподаватель. На слайде даны векторы. Верно ли найдены координаты векторов?
Задание на слайде.
Даны точки
Координаты векторов:
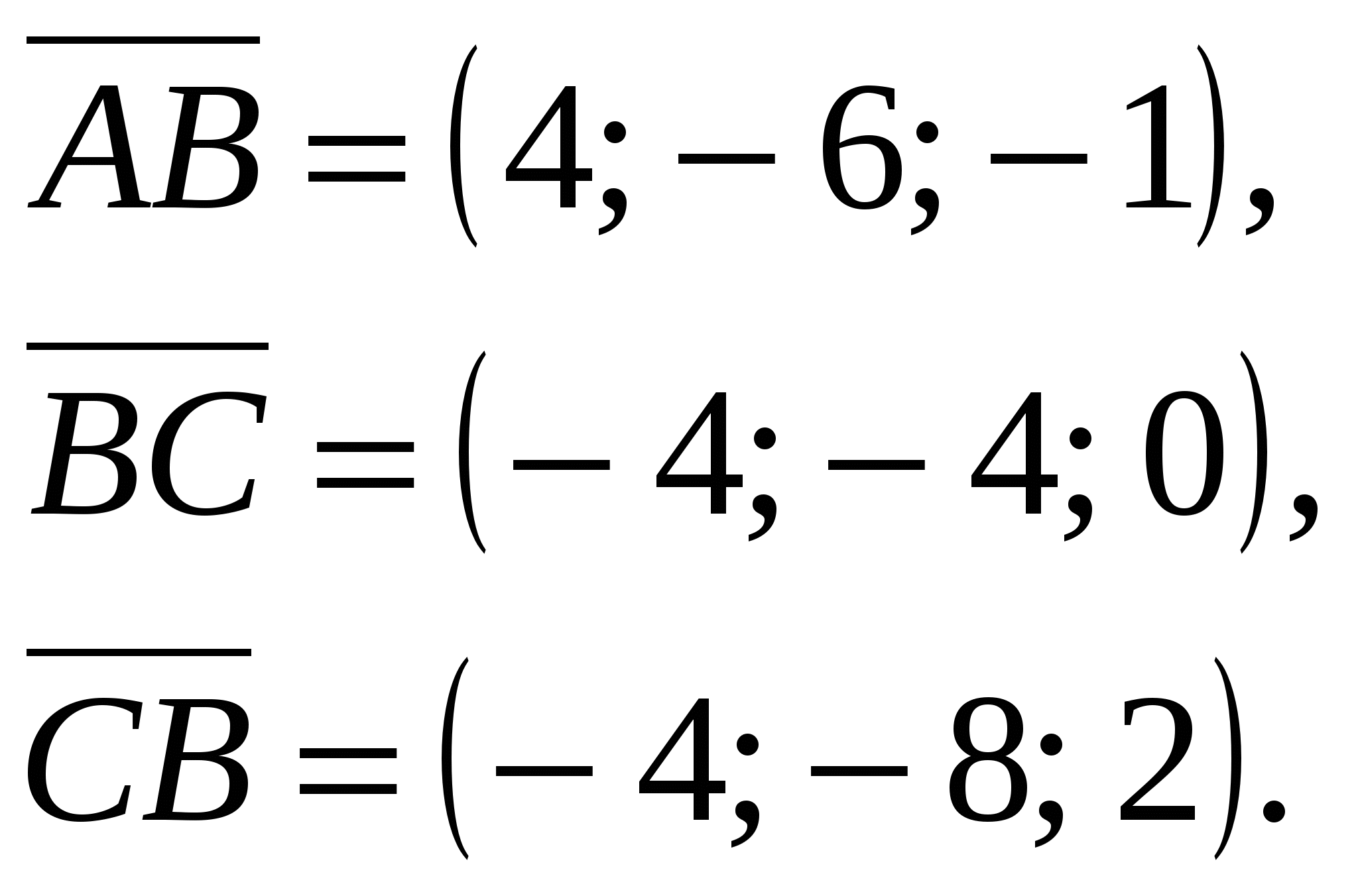
5. Что такое абсолютная величина вектора? (Длина отрезка, изображающего вектор. Запись:
6. Какие векторы называются равными? (Векторы, которые сонаправленные и имеют равные длины. Запись: