Практическое занятие 2. Стоимость заемного капиталаЗадание1.Вам поручено провести анализ досрочно погашаемой корпоративнойоблигации с номиналом 1000 рублей и 12% ставкой купона, которыйвыплачивается раз в год, со сроком до погашения 20 лет и условиемдосрочного выкупа не ранее, чем через 4 года по курсу 112% номинала.Текущий курс облигации 116% от номинала.Требуется определить:a. текущую доходность облигацииb. приблизительную доходность к погашениюc. полную доходность к погашениюd. приблизительную доходность к досрочному погашению (отзыву)e. полную доходность к досрочному погашению (отзыву).Решение:Для решения данной задачи используем формулы расчета приблизительных доходностей. Текущая доходность (CY, current yield) –может быть посчитана для любой купонной облигации как отношение годовой суммы купонных выплат к текущей рыночной цене облигации.

1. 
   Определим текущую доходность облигации:
   

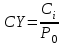
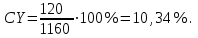
С – величина купонных выплат за год;P₀–текущая рыночная стоимость (цена приобретения) облигации.Купон – 120 руб., рыночный курс – 1160 руб. Текущая доходность облигации равна – 10,34%.

2. 
   Далее определим приблизительную доходность к погашению:
   

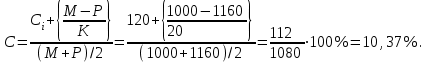
где, M – номинал облигации; P – текущая цена (на момент оценки); C – купонный доход; K – число лет, оставшихся до погашения облигации.Таким образом, приблизительная доходность к погашению равна – 10,37%.

3. 
   Полную доходность к погашению определим по формуле:
   

4. 
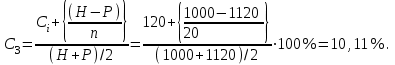
   Приблизительная доходность к погашению.
   

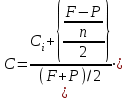
При этом: купон 120 руб., курс – 1160 руб., курс отзыва – 1120 руб., лет к погашению – 4.

---

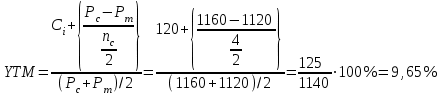
Согласно формуле приблизительная доходность к погашению равна 9,65%.

5. 
   Полная доходность к досрочному погашению (отзыву).
   

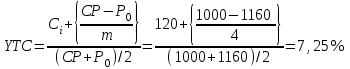
Цена отзыва облигации - та сумма денег, которую заплатит эмитент, чтобы произвести отзыв облигации. Когда облигация в первый раз становится подлежащей выкупу, досрочная цена часто равна номинальной стоимости плюс проценты за один год.Доходность к отзыву –показатель, который аналогичен доходности к погашению, но может быть посчитан только для отзывных облигаций:Где: YTC –доходность к отзыву за расчетный период (например, год);С – величина купонных выплат за расчетный период (например, год);CP –цена отзыва (сумма, которая выплачивается при досрочном погашении);P₀–текущая рыночная стоимость (цена приобретения) облигации;m –количество периодов (лет), оставшихся до окончания защиты от отзыва (досрочного погашения).Таким образом, по расчетам были определены:

1. 
   текущая доходность облигации - 10,34%;
   
2. 
   приблизительная доходность к погашению - 10,37%;
   
3. 
   полная доходность к погашению - 10,11%;
   
4. 
   приблизительная доходность к досрочному погашению (отзыву) - 9,65%;
   
5. 
   полная доходность к досрочному погашению (отзыву) - 7,25%.
   

Практическое занятие 2. Стоимость заемного капиталаЗадание 5.1 000 рублевая облигация с 8 - процентным купоном продается на рынке с дисконтом в 10%, со сроком обращения 3 года. Определите текущую доходность облигации и доходность к погашению.Решение:Дано: Облигация номиналом в 1000 рублей и купонной ставкой 8%, срок обращения 3 года, цена на рынке = 1000 – 10% = 900 рублейТекущая доходность облигации = купонная доходность/чистая цена облигации*100%Текущая доходность облигации = 80/900*100%=8,88%Доходность к погашению = Доход от облигации за весь срок (проценты+дисконт)/Текущая стоимость* 365/Количество дней до погашения * 100%Доходность к погашению: (80+80+80)/900*365/1095*100%=8,88%Ответ: текущая доходность облигации = 8,88%, доходность к погашению = 8,88%Практическое занятие 1. Стоимость собственного капиталаЗадание 2.Текущая цена акций компании составляет 11,1 руб. Прибыль и дивиденды в следующем году должны составить 2 и 1 руб. соответственно. Инвесторы ожидают бессрочный рост компании с темпом 3% в год. Требуемая доходность со стороны инвесторов составляет 12%.

---

Определите:

1. 
   Справедливую стоимость акции компании.
   

Используем модель непрерывного роста (модель Гордона) для определения справедливой стоимости акции компании. Стоимость акции = D₁ / (k - g), где: D₁ = ожидаемый годовой дивиденд на акцию в следующем годуk = ставка дисконтирования или требуемая норма прибыли g = ожидаемый темп роста дивидендовСправедливая стоимость акции = 1/(0,12-0,03)=11,1 руб.Таким образом, согласно модели, текущая цена акций компании является справедливой в данных условиях и при стабильном росте дивидендов.

2. 
   Предположим, что компания объявляет о том, что она будет выплачивать всю чистую прибыль в виде дивидендов, финансируя рост за счет дополнительных эмиссий акций. Как это решение повлияет на цену акций?
   

Решение о дополнительной эмиссии акций данной компании никак не повлияет на цену акции, т.к. текущая цена акций равна справедливой стоимости акции, рассчитанной раннее.

3. 
   Может ли этот пример служить доказательством тезиса о том, что дивидендная политика «бессмыслена», другими словами, не значима?
   

Я не могу согласится с данным тезисом, т.к. дивидендная политика помогает найти оптимальное решение для собрания участников (учредителей, акционеров) в данный момент времени, а также достигнуть поставленных целей. При дополнительной эмиссии акций, компания проводит демонстрацию намерений — стремление привлечь инвесторов, повысить рыночную стоимость и ликвидность акций за счет объявления повышенных дивидендов. Но в то же время, данное решение уменьшит накопленную прибыль компании, что снижает капитализацию и лишает компанию возможности использовать эти средства на развитие.Практическое занятие 3. Инвестиционная деятельность корпорации. Стоимость капиталаЗадание 2.Проект А требует инвестиций в размере 100 тыс. дол. и будет приносить по оценке аналитиков ежегодные чистые денежные поступления на шестилетнем отрезке времени в размере 31 тыс. дол. Проект Б требует инвестиций в размере 300 тысяч и годовые инвестиции в течение шести лет составят 85 тыс. дол. Стоимость капитала компании, рассматривающей инвестиционный проект равна 14% годовых. Какой проект должен быть принят для максимизации рыночной оценки компании, если

---

1) проекты независимы, 2) проекты альтернативные (может быть принят только один), 3) при ограниченности капитала (существуют нефинансовые ограничения), 4) стоимость капитала компании не может быть точно определена, но есть приблизительные оценки диапазона изменений (порядка 16-17% годовых), 5) стоимость капитала компании 10%, проекты альтернативные и ставка реинвестирования поступлений от ранее принятых проектов равна 14%. Объясните, что понимается под финансовыми ограничениями по привлечению капитала и что под нефинансовыми.Решение:Рассчитаем NPV инвестиционного проекта по формуле: 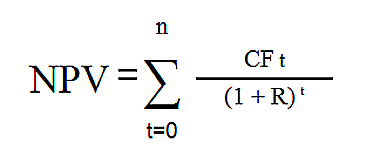, где:n, t — количество временных периодов,CF — денежный поток,R — стоимость капиталаРасчет NPV для проекта А можно посмотреть в таблице:

Год	Проект А	Ставка 14%	Фактор	Сумма
0	(100)	1	1	(100)
1	31	1/(1,14)1	0,877	27,187
2	31	1/(1,14)2	0,769	23,839
3	31	1/(1,14)3	0,675	20,925
4	31	1/(1,14)4	0,592	18,352
5	31	1/(1,14)5	0,519	16,089
6	31	1/(1,14)6	0,456	14,136
Итого	186			20,528

Расчет NPV для проекта Б можно посмотреть в таблице:

Год	Проект Б	Ставка 14%	Ф актор	Сумма
0	(300)	1	1	(300)
1	85	1/(1,14)1	0,877	74,545
2	85	1/(1,14)2	0,769	65,365
3	85	1/(1,14)3	0,675	57,375
4	85	1/(1,14)4	0,592	50,32
5	85	1/(1,14)5	0,519	44,115
6	85	1/(1,14)6	0,456	38,76
Итого	510			30,48

---

1. Оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.2. Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект Б, поскольку его NPV заметно больше 30,48, чем NPV Проекта А 20,528.3. Чисто теоретически выбор ограниченного капитала противоречит цели максимизации рыночной оценки капитала, так как максимум будет достигаться при принятии всех проектов с положительным значением ЧДД.Лимитирование означает отказ от некоторых прибыльных проектов и принятие лучших из них, удовлетворяющих ограничению капитала. Наиболее простой метод — ранжирование проектов с равными инвестиционными затратами по убыванию ЧДД и выбор из списка проектов с наибольшим значением, пока позволяет ограниченный размер капитала. Если проекты различаются инвестиционными затратами и лучшие проекты являются более дорогостоящими (как в нашем случае), то реальный выбор может осуществляться по критерию наибольшего значения индекса рентабельности.Индекс рентабельности рассчитывается по формуле:PI(A) = 120,549/100 = 1,205PI(Б) = 330,537/300 = 1,102По максимальному индексу рентабельности выбираем проект А4. Рассчитаем NPV для данных проектов при ставке дисконта 16% и 17%

Стоимость капитала, %	NPV(A)	NPV(Б)
16	14,204	13,14
17	11,29	5,15

Анализ различных сценариев позволяет выбрать менее рискованный проект. Согласно полученным результатам, значения NPV(A) при стоимости капитала 16% и 17% значительно больше, чем у проекта Б, следовательно, при данных условиях следует выбрать проект А.5. В данном случае необходимо рассчитать модифицированную внутреннюю норму доходности (MIRR)­ – данный показатель отражает минимальный внутренний уровень доходности проекта при осуществлении реинвестиций в проект. Данный проект использует процентные ставки, полученные от реинвестирования капитала. Формула расчета модифицированной внутренней нормы доходности:

---

Смотрите также файлы

• Практикум для среднего профессионального образования под редакцией И. И. Елисеевой. 3е изд., перераб и доп. Москва.pdf

• Общество с ограниченной ответственностью обратилось в арбитражный суд с иском к индивидуальному предпринимателю о взыскании компенсации за незаконное использование фонограмм, права на которые принадлежат истцу.docx

• Образовательная программа Цифровые маркетинговые коммуникации.docx

• Рабочая программа практики.docx

• Исследования Характеристики разговорного английского языка.docx