Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 137
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– безразмерное время (критерий Фурье); α – коэффициент теплоотдачи от восходящего потока в горные породы (на стенке скважины), Вт/(м2·0C); 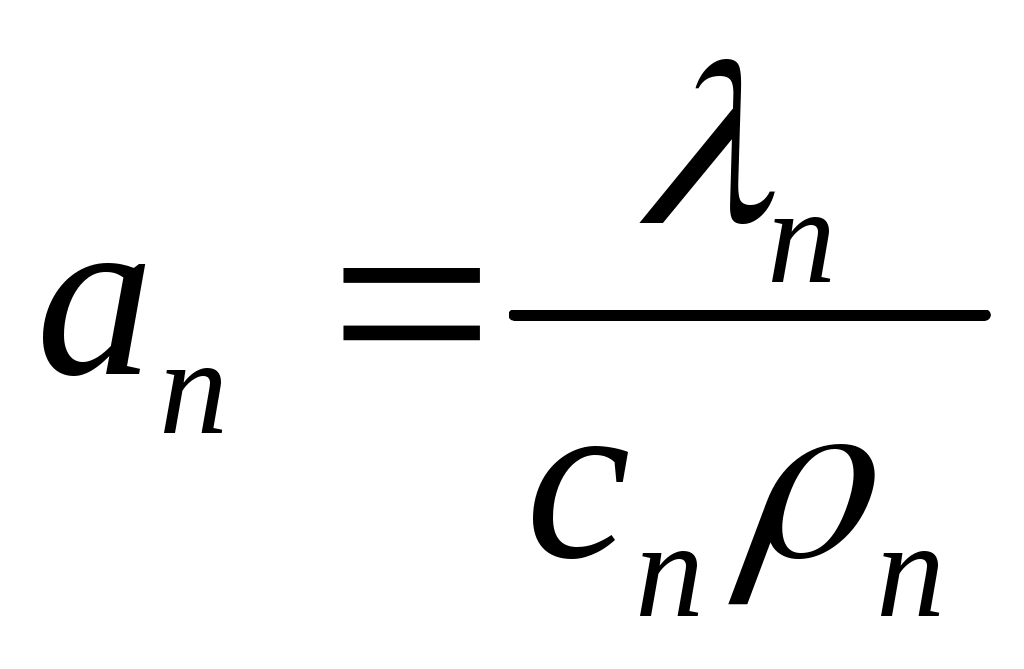 – коэффициент температуропроводности пород, м2/с; λп – коэффициент теплопроводности пород, Вт/(м·0C); cп – удельная массовая теплоемкость породы, Дж/(кг·0C); ρп – плотность породы, кг/м3; τ – продолжительность циркуляции, с; R0 – радиус скважины, м.
– коэффициент температуропроводности пород, м2/с; λп – коэффициент теплопроводности пород, Вт/(м·0C); cп – удельная массовая теплоемкость породы, Дж/(кг·0C); ρп – плотность породы, кг/м3; τ – продолжительность циркуляции, с; R0 – радиус скважины, м.
Для зависимости существует точное, но очень сложное аналитическое выражение.
существует точное, но очень сложное аналитическое выражение.
При выводе формул для kτи kагр средняя температура очистного агента считалась постоянной, точнее, медленно изменяющейся со временем (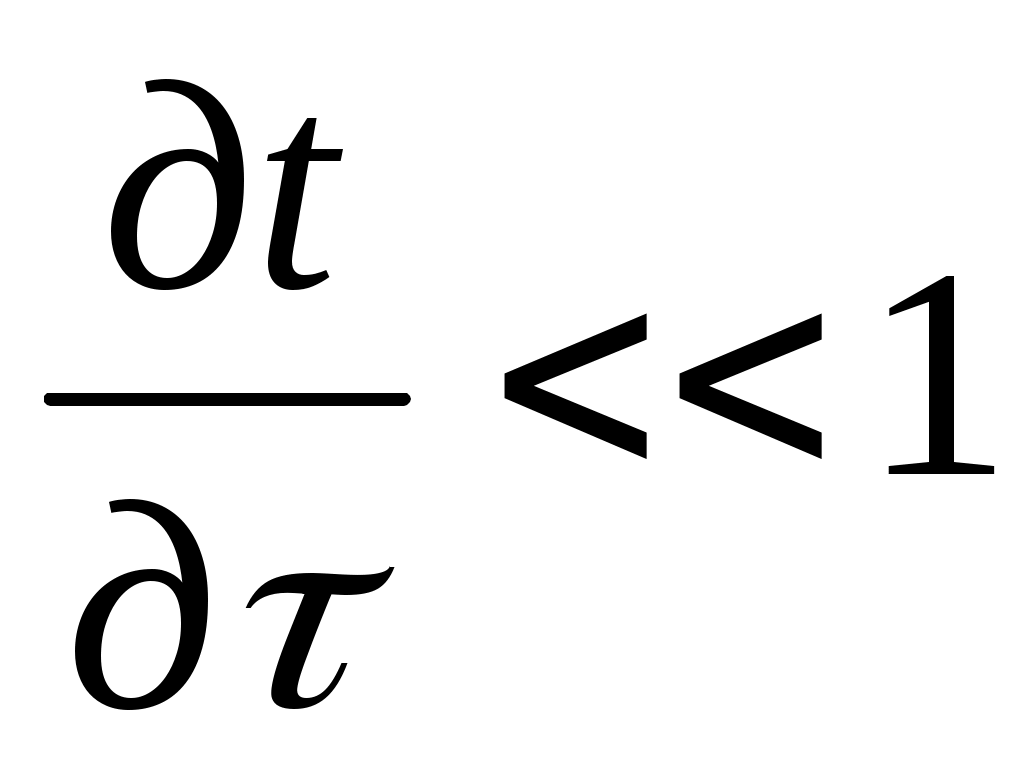 ). Если при расчете температуры очистного агента использовать среднее за период теплообмена значение температуры, то погрешность компенсируется применением среднеинтегрального значения kτ.
). Если при расчете температуры очистного агента использовать среднее за период теплообмена значение температуры, то погрешность компенсируется применением среднеинтегрального значения kτ.
Упрощенные зависимости для kτ
Для отдельных достаточно больших значений F0 формулы могут быть получены на основе общего выражения
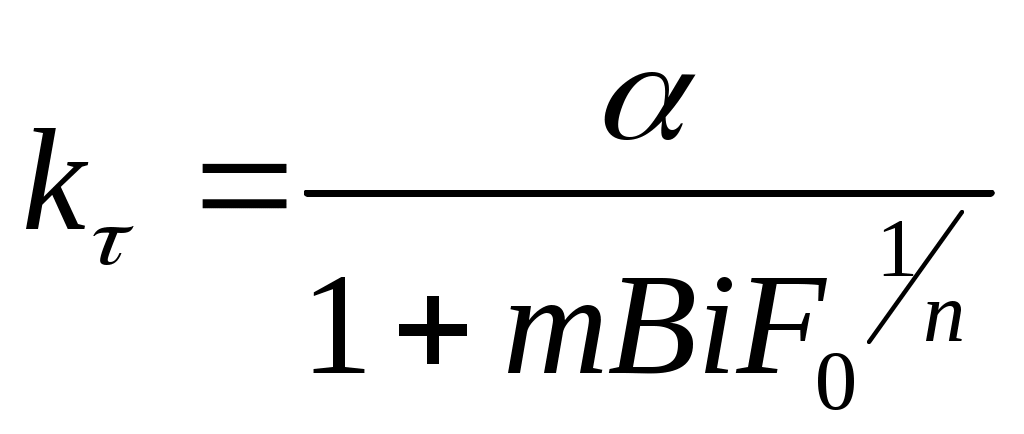 , (17а)
, (17а)
где m>0, n≥1 (целое).
Для условий бурения скважин в большинстве случаев пригодна зависимость
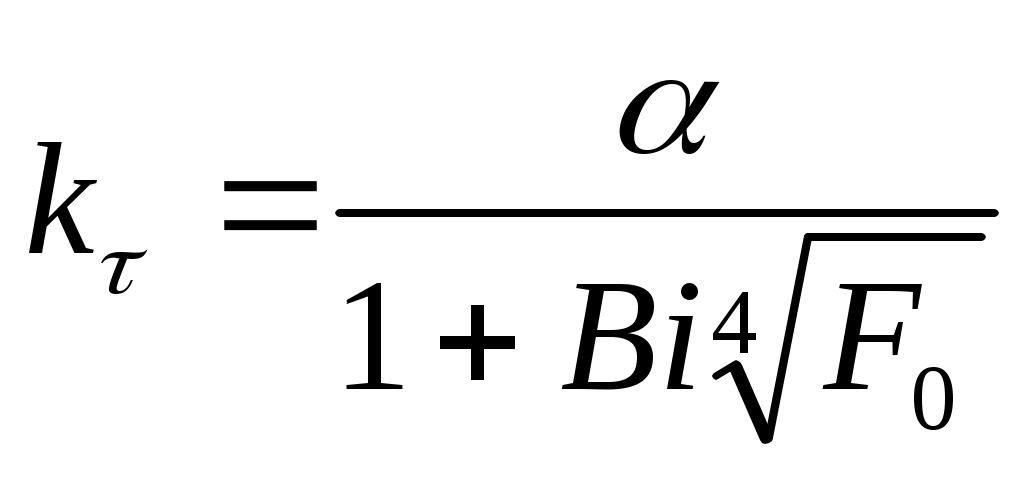 . (18)
. (18)
При больших значениях Bi, характерных для условий бурения с промывкой водой и глинистыми растворами, можно использовать выражение
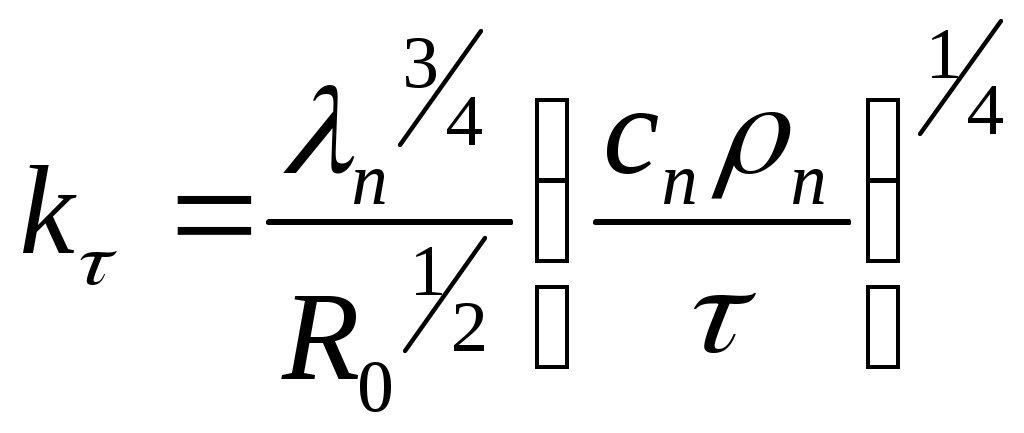 , (19)
, (19)
где cп – удельная массовая теплоемкость породы, Дж/(кг·0C).
Среднеинтегральный по времени коэффициент нестационарного теплообмена можно получить из (18) с помощью теоремы о среднем
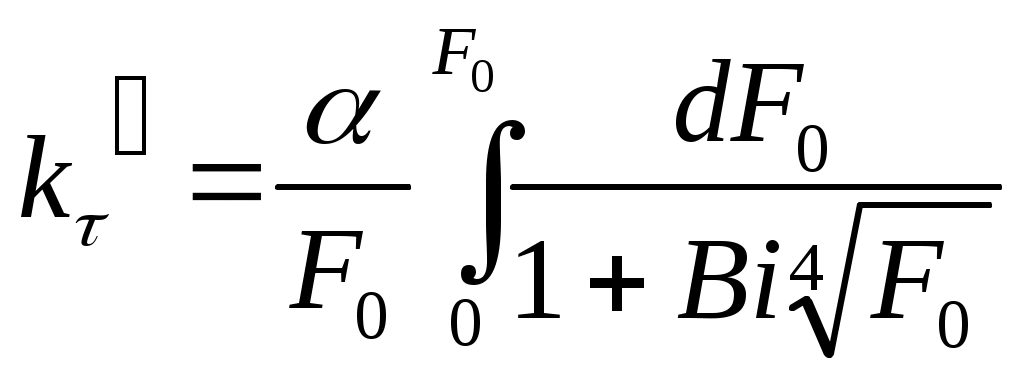 . (20)
. (20)
Решением выражения (20) является
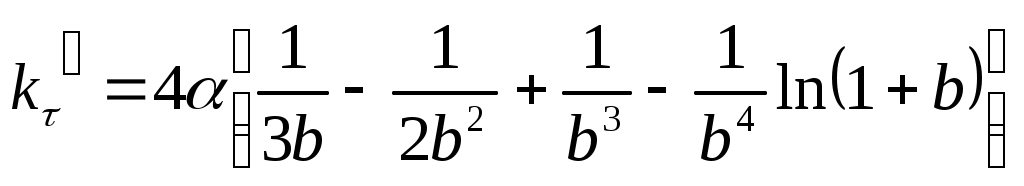 , (21)
, (21)
где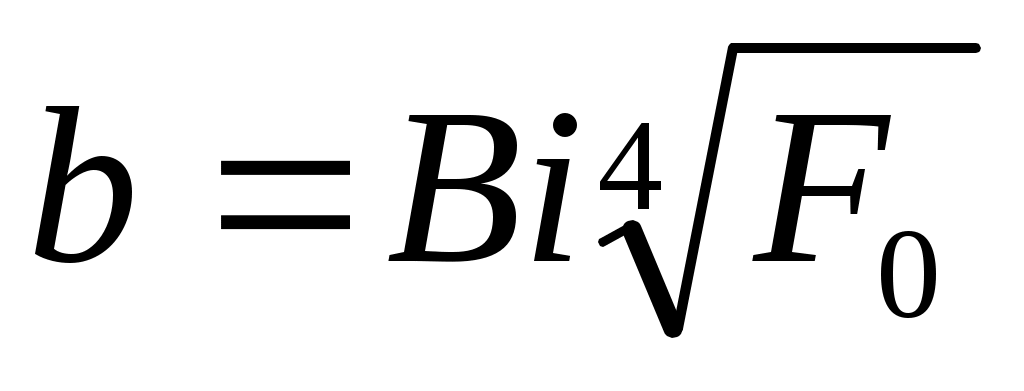 .
.
При бурении с промывкой водой и глинистыми растворами, при бурении с продувкой, когда b≥2, можно использовать простейшее выражение
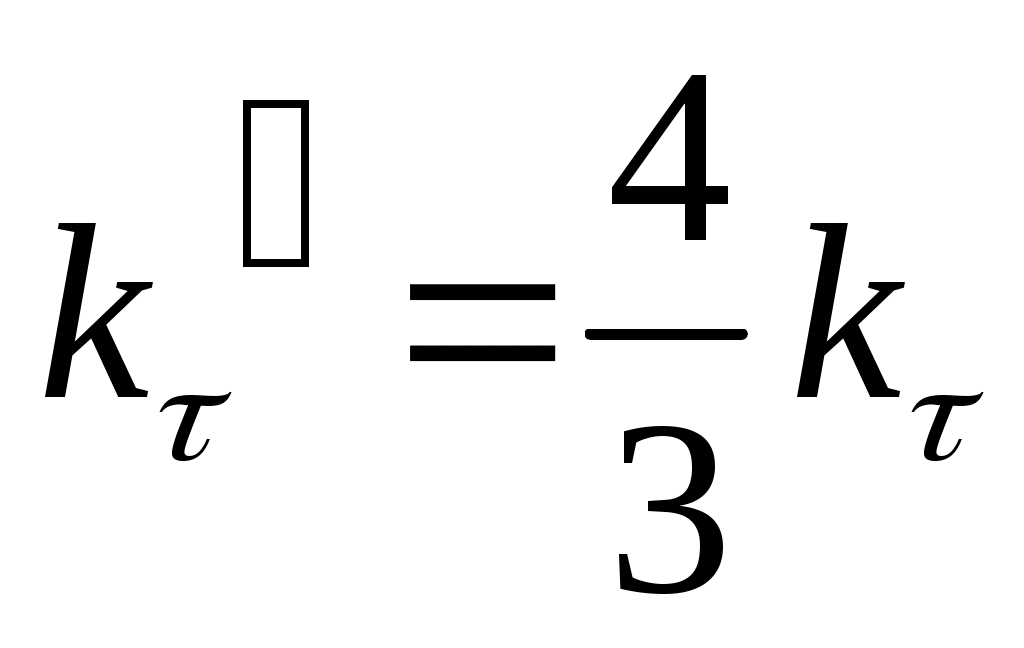 (22)
(22)
Гидравлический уклон в бурильных трубах i1 и в кольцевом канале скважины i2 определяется из выражения
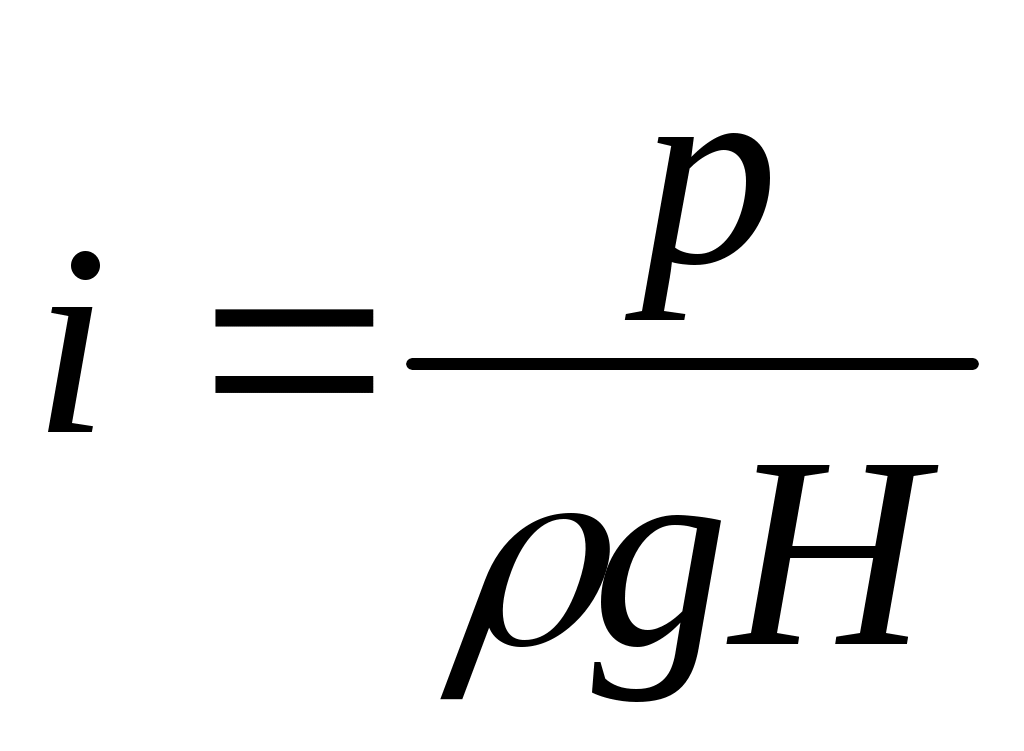 , (23)
, (23)
где p(требуют расчета!) – потери давления в соответствующем канале, Па; ρ – плотность очистного агента (для газа – при средних значениях температуры и давления в канале), кг/м3; H – глубина скважины, м.
Прирост температуры очистного агента за счет теплоты, генерируемой породоразрушающим инструментом
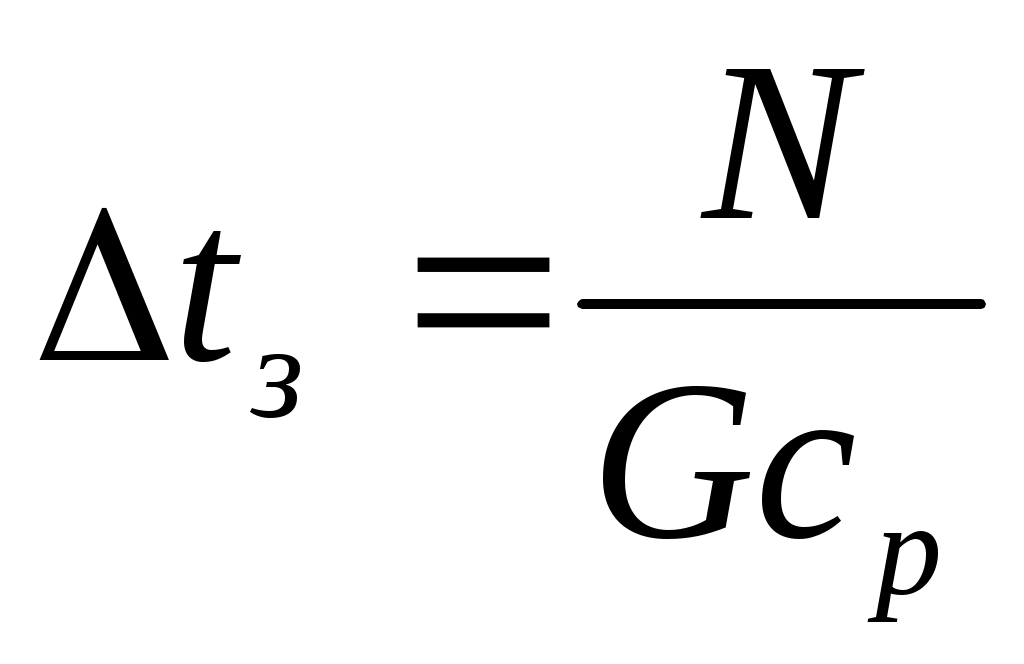 , (24)
, (24)
где N – мощность, реализуемая на забое, Вт.
Коэффициент теплопередачи через стенку бурильных труб, отнесенный к 1м труб
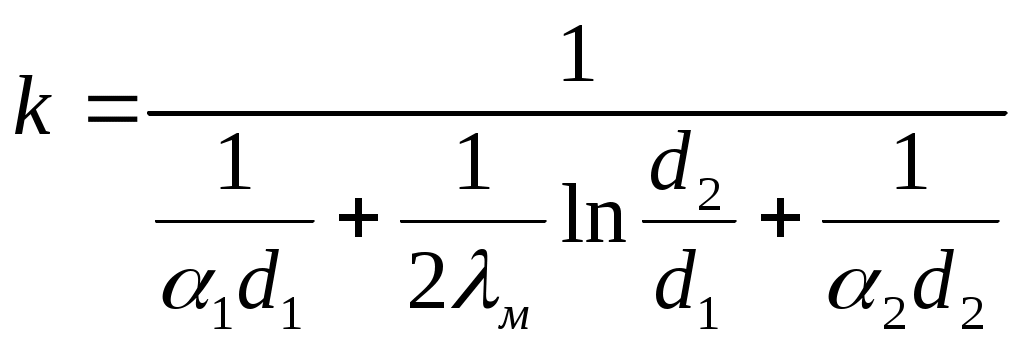 ,
, 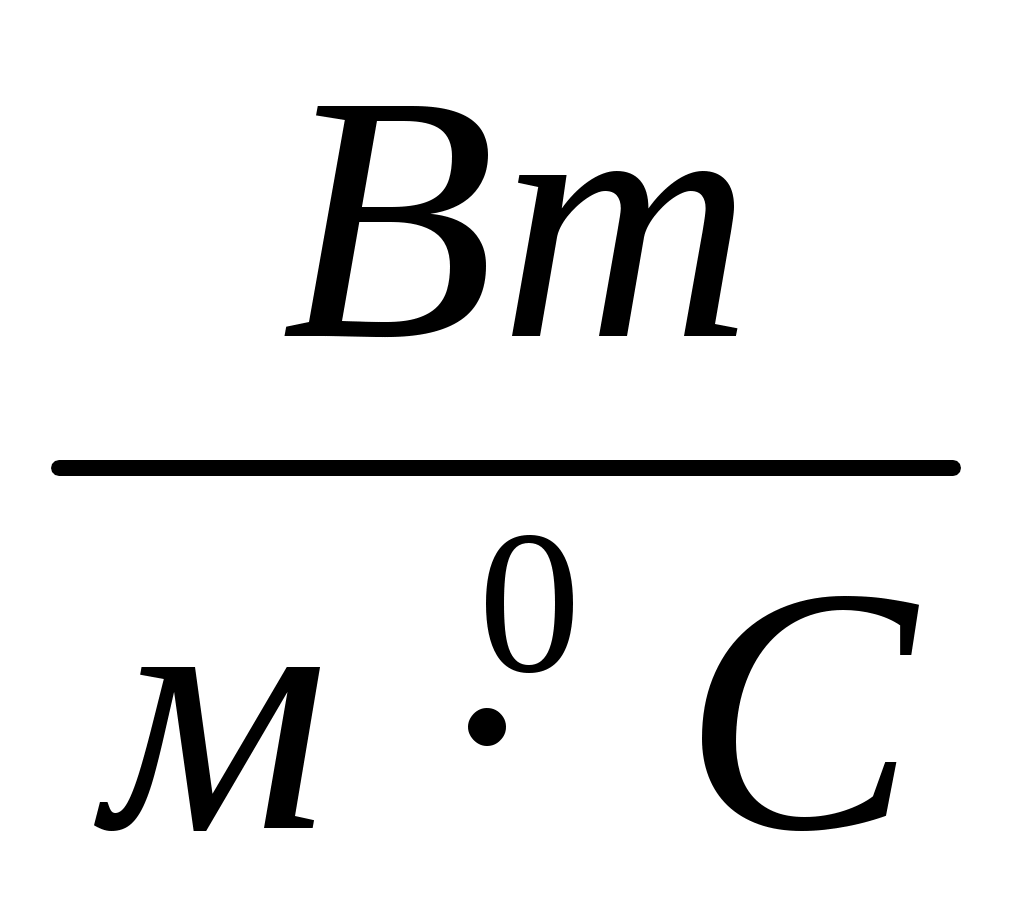 (25)
(25)
где d1, d2 – внутренний и наружный диаметры труб, м; α1, α2– коэффициенты теплоотдачи соответственно во внутреннем канале бурильных труб и в кольцевом канале скважины, Вт/(м2·0C); λм – коэффициент теплопроводности материала труб, Вт/(м·0C).
Для теплоизолированных труб используется аналогичная по структуре формула для многослойной цилиндрической стенки. Так, для труб, покрытых внутри слоем теплоизолятора
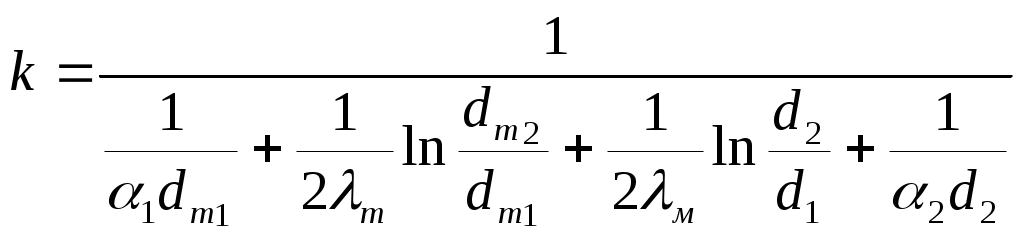 . (26)
. (26)
Индекс “т” означает теплоизолирующий слой.
Коэффициент теплоотдачи α определяется через критерий Нуссельта Nu
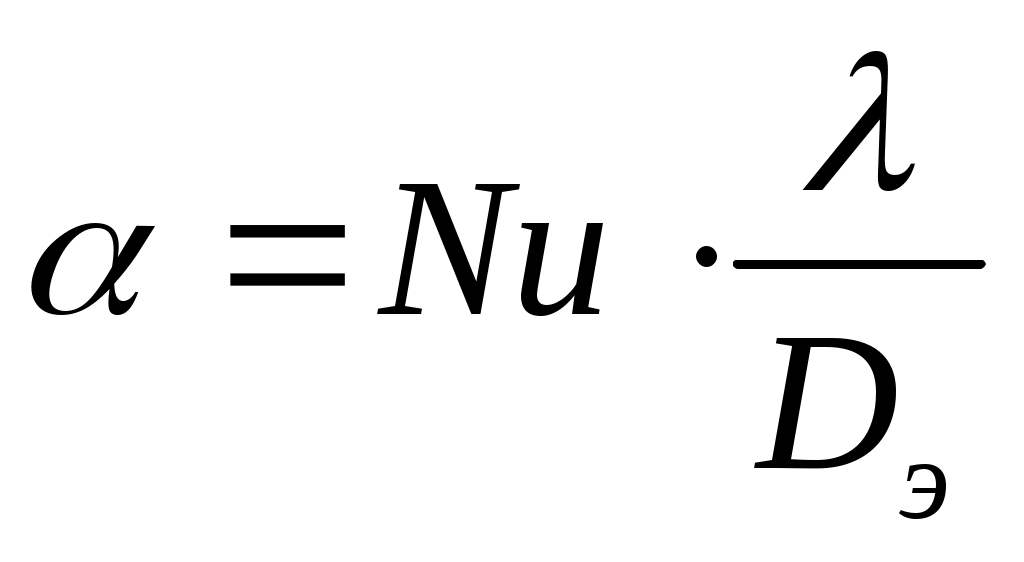 , (27)
, (27)
где λ – коэффициент теплопроводности очистного агента, Вт/(м·0C).
При ламинарном течении ньютоновских сред (вода, воздух, солевые растворы)
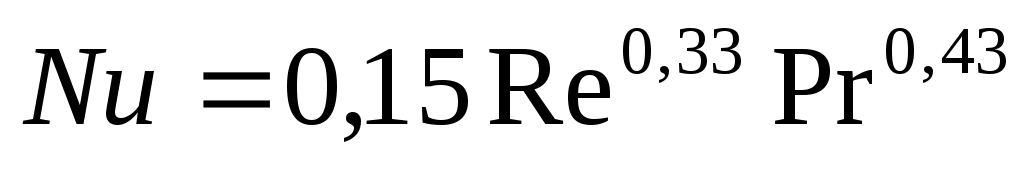
,
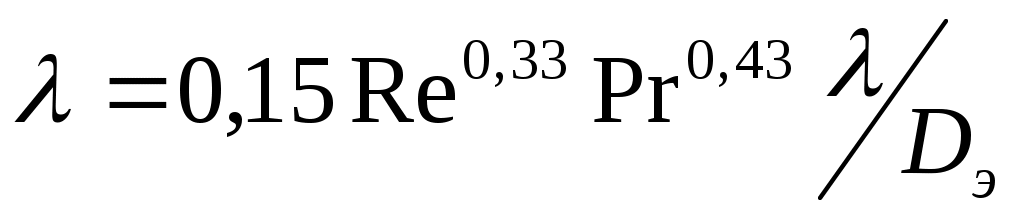 , (28)
, (28)
где Pr – критерий Прандтля для очистного агента
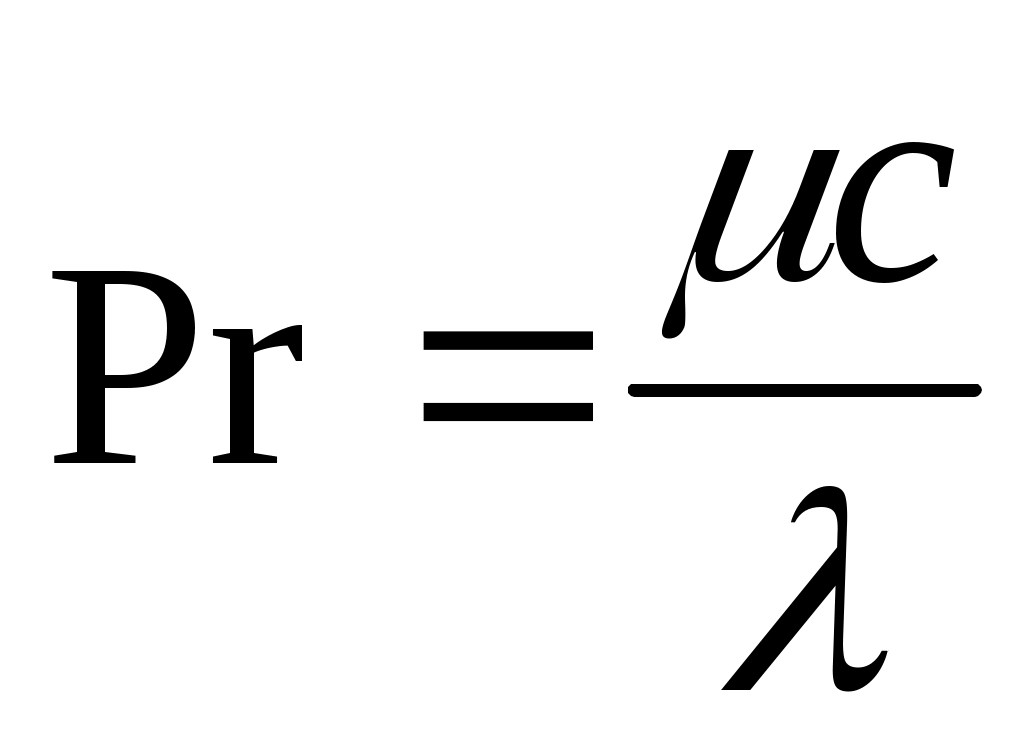 , (29)
, (29)
где μ – коэффициент динамической вязкости очистного агента, Па·с; c – удельная массовая теплоемкость, Дж/(кг·0C).
При турбулентном течении ньютоновских сред
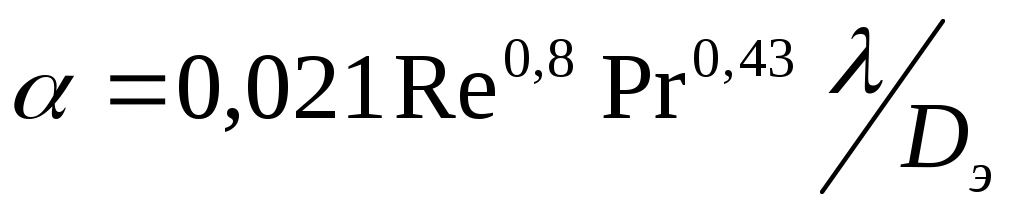 . (29а)
. (29а)
При бурении с продувкой воздухом можно использовать зависимость
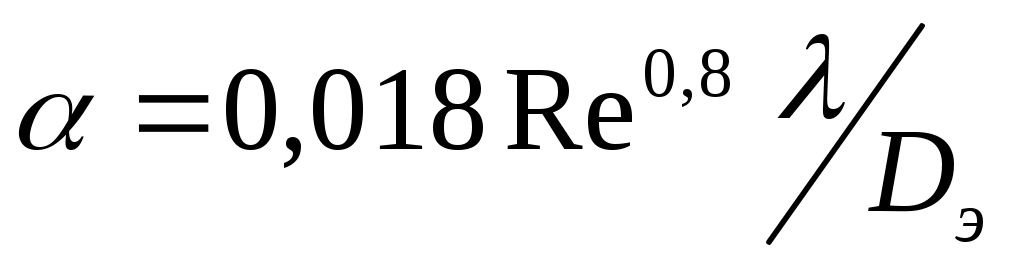 (30)
(30)
Определение α при движении неньютоновских сред затруднено.
Для глинистого раствора в первом приближении можно пользоваться формулой академика Л.С. Лейбензона
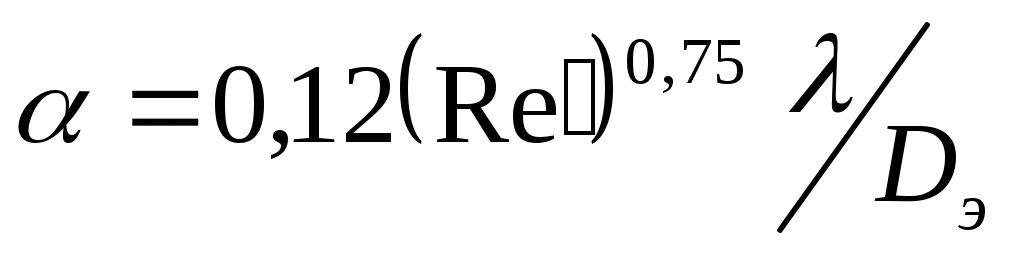 , (31)
, (31)
где Re′ – обобщенный параметр Рейнольдса
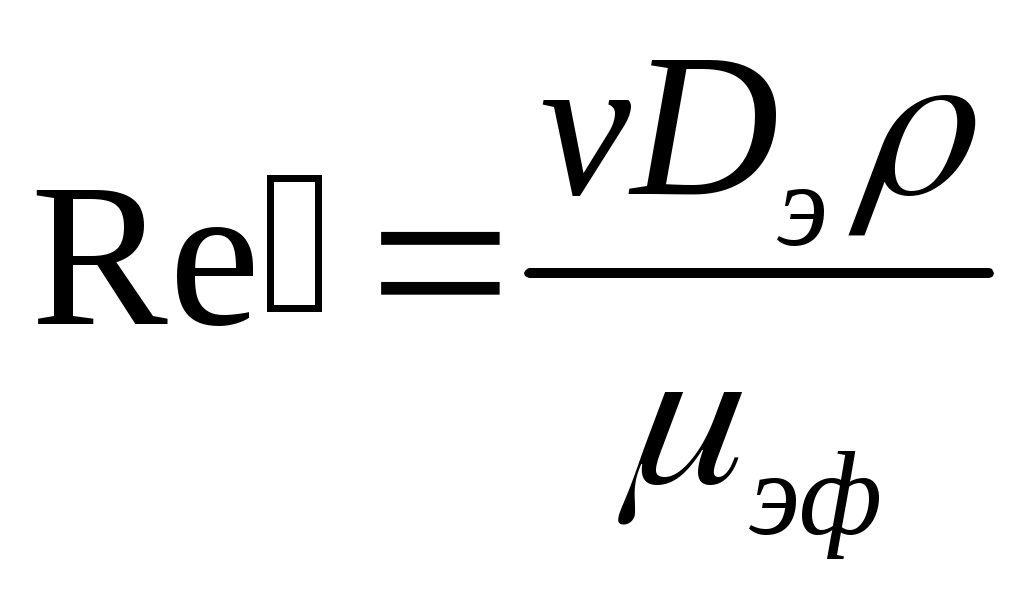 (32)
(32)
В дальнейшем апостроф будем опускать.
При турбулентном течении глинистого раствора в трубах можно использовать формулу Б.И. Есьмана
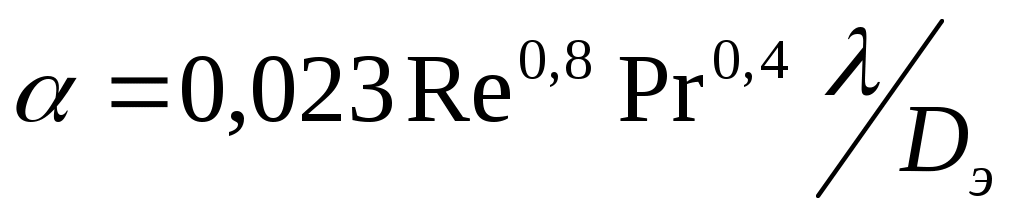 . (33)
. (33)
В формуле (33) обобщенный параметр Прандтля определяется через µэф
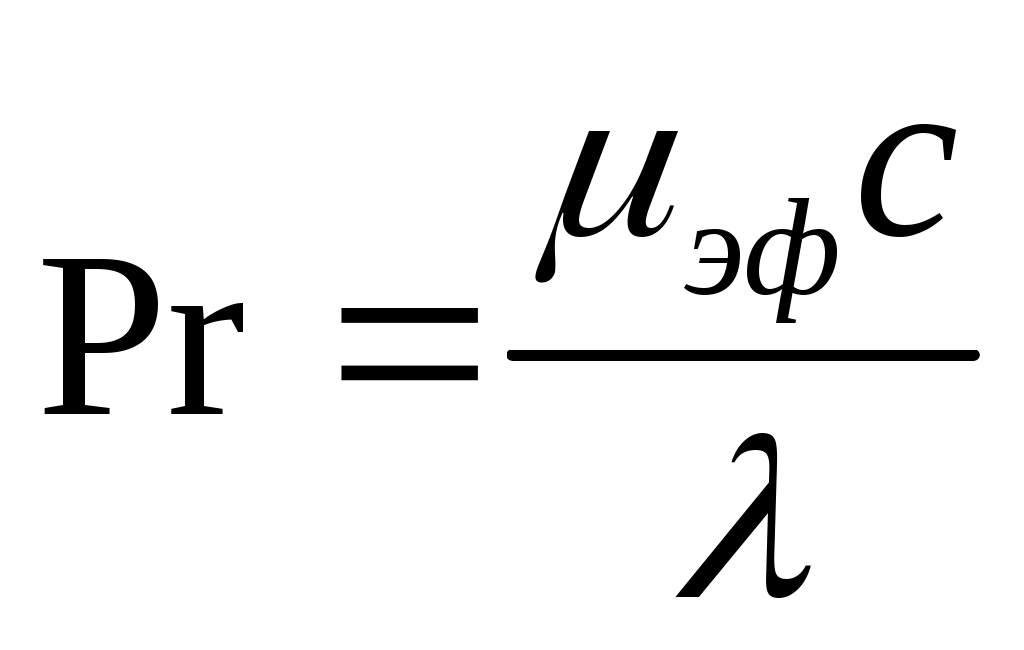 ; (34)
; (34)
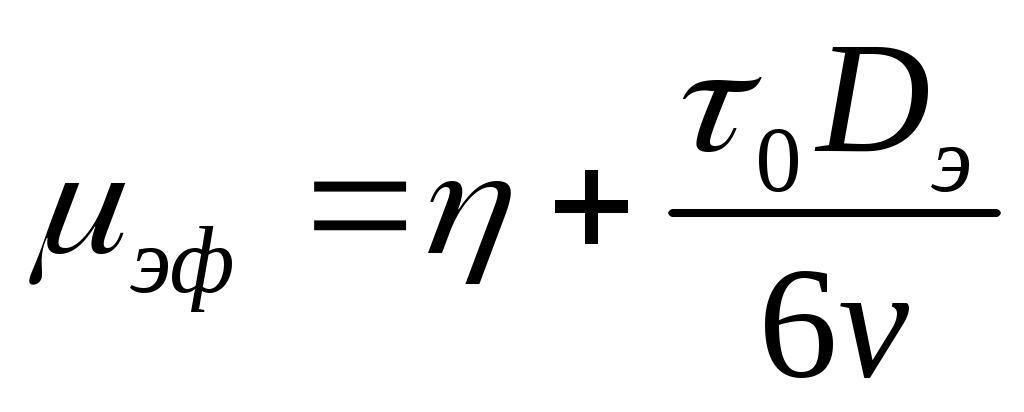 (35)
(35)
Теплоотдача глинистого раствора при течении в кольцевых каналах изучена недостаточно. При турбулентном течении (Re≥10000) Ю.М. Проселков рекомендует формулу
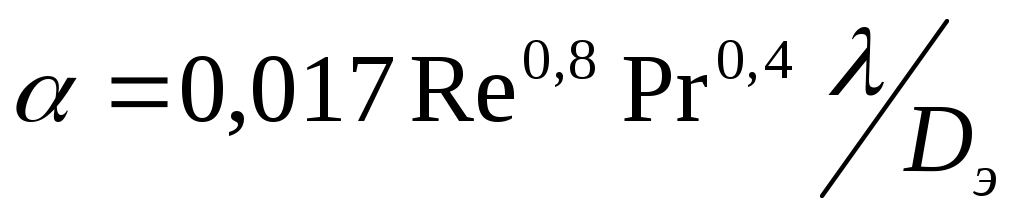 (36)
(36)
При ламинарном течении глинистых растворов, в первом приближении, возможно использование зависимости (28) с заменой Re и Pr на Re′ и Pr′ (через µэф)/
Коэффициент kагр может быть определен по формуле Ю.Д. Дядькина
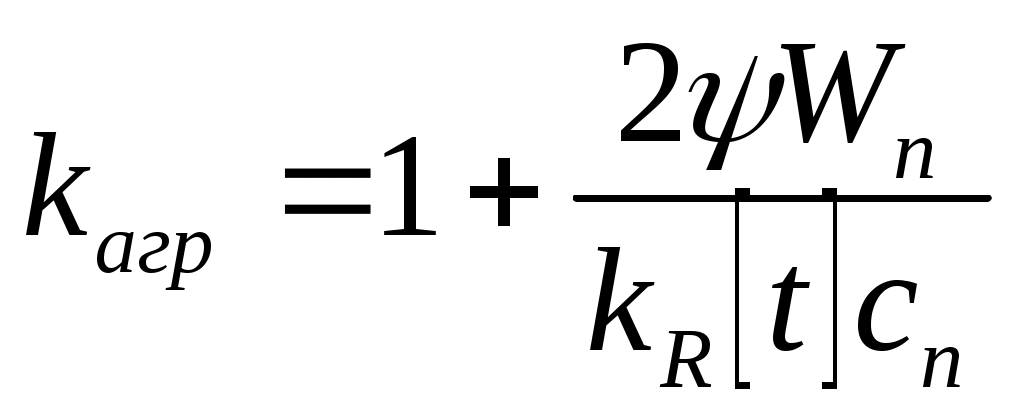 (37)
(37)
где ψ – удельная теплота плавления льда (кристаллизации воды), Дж/кг; Wп – активная массовая влажность породы (отношение массы льда или свободной воды в единице объема породы к ее объемной плотности), доли ед
.; [t] – абсолютное значение температуры очистного агента в кольцевом канале скважины, осредненное по протяженности расчетного участка и длительности циркуляции, 0C; kR – безразмерный коэффициент, зависящий от характера распределения температуры вокруг скважины.
Если принять kR=4,8 и ψ=3,34·105 Дж/кг, то
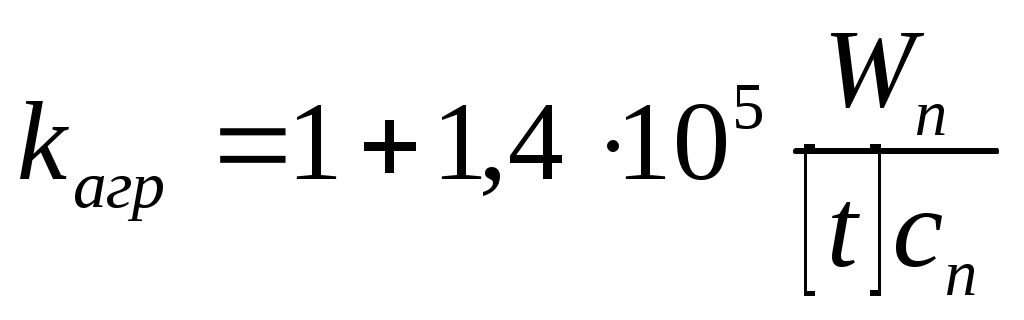 (38)
(38)
Тепло- и массообмен в призабойной зоне скважины
При работе породоразрушающего инструмента на забое выделяется теплота. По данным Л.А. Шрейнера физ. КПД разрушения пород составляет не более 0,01%, т.е., практически вся механическая энергия рассеивается в виде теплоты.
При установившемся режиме, когда породоразрушающий инструмент нагреется до постоянной температуры, количество теплоты, выделяющейся на забое в единицу времени, равно количеству теплоты, воспринимаемой очистным агентом.
Рисунок …
При бурении по “сухим” породам
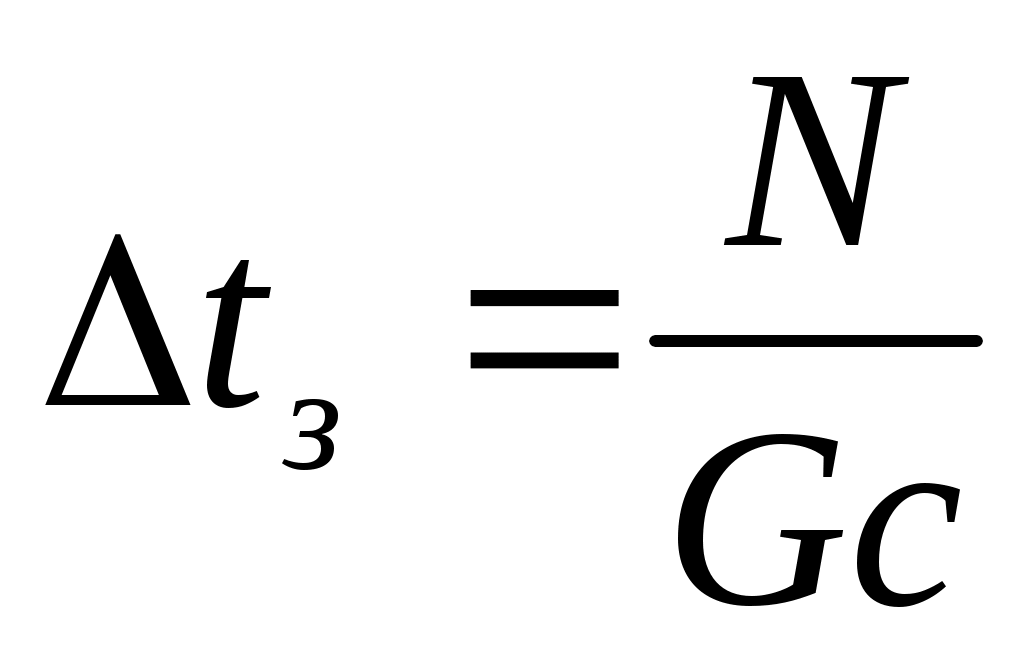 .
.
При бурении с продувкой во влажных мерзлых породах теплота, генерируемая породоразрушающим инструментом, затрачивается на нагрев воздуха, шлама, плавление льда и испарение влаги.
Пренебрегая теплотой на нагрев шлама,
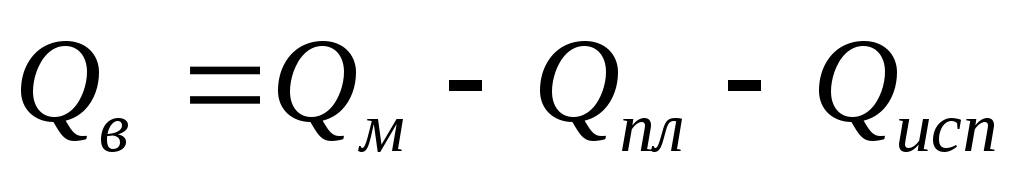 , (39)
, (39)
где Qм – количество теплоты, генерируемой инструментом, в единицу времени, Вт; Qпл, Qисп - количество теплоты, генерируемой инструментом, в единицу времени на плавление льда и испарение влаги, Вт.
При бурении с продувкой крайне желательно, чтобы вода не выделялась на забое в виде жидкой фазы (сальники), т.е., можно допустить плавление и испарение в единицу времени такого количества льда, которое могло бы довести воздух до 100-%-ной влажности. При движении воздуха к устью происходит его охлаждение и влага будет выпадать в виде инея и снега.
Поскольку насыщение воздуха до 100% возможно только за счет льда, количество теплоты на его плавление
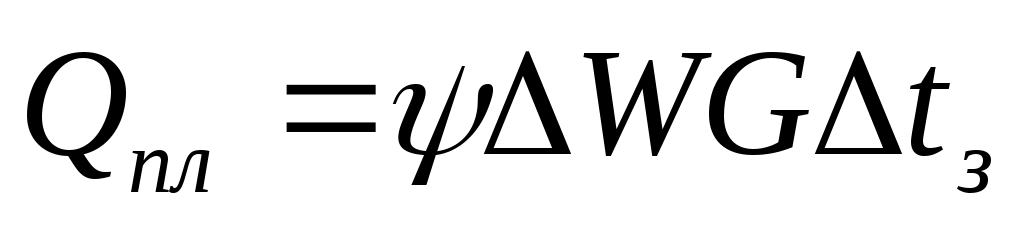 , (40)
, (40)
и на испарение
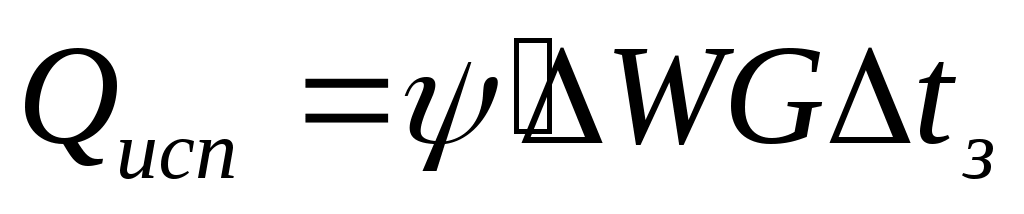
, (41)
где ψ и ψ′ – скрытая теплота плавления льда и парообразования, Дж/кг; ΔW – температурный прирост влагосодержания воздуха, кг/(кг·0C).
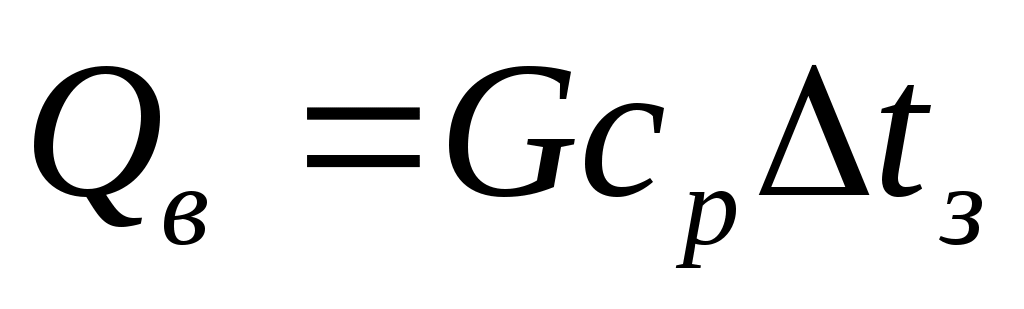 ; (42)
; (42)
Будем считать, что вся механическая работа на забое рассеивается в форме тепла (Qм=N). Подставим (40) и (41) в (39)
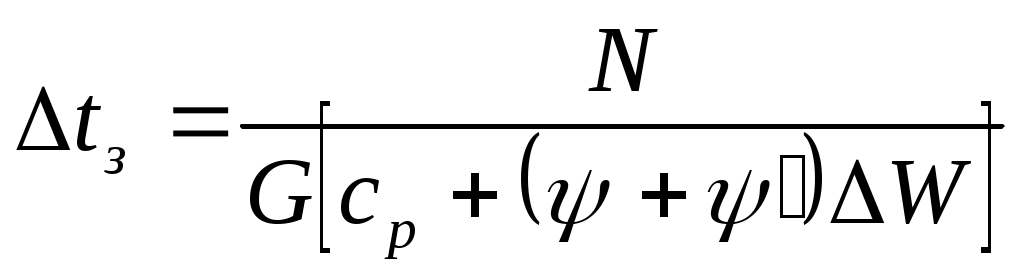 . (43)
. (43)
В случае бескернового бурения с большими механическими скоростями необходимо учитывать теплоту на нагрев шлама.
Для предупреждения растепления мерзлых пород сжатый воздух необходимо охлаждать. Влажность воздуха в призабойной зоне с большим запасом можно принять равной 10%.
При изменении относительной влажности воздуха от 10% до 100% в интервале температур –100C÷+100C, средний прирост его влагосодержания ΔW=0,00033 кг/(кг·0C). ψ=3,34·105 Дж/кг, ψ′=2,49·106 Дж/кг, cp=1·103 Дж/(кг·0C). Подставив эти значения в (43), получим приближенную формулу:
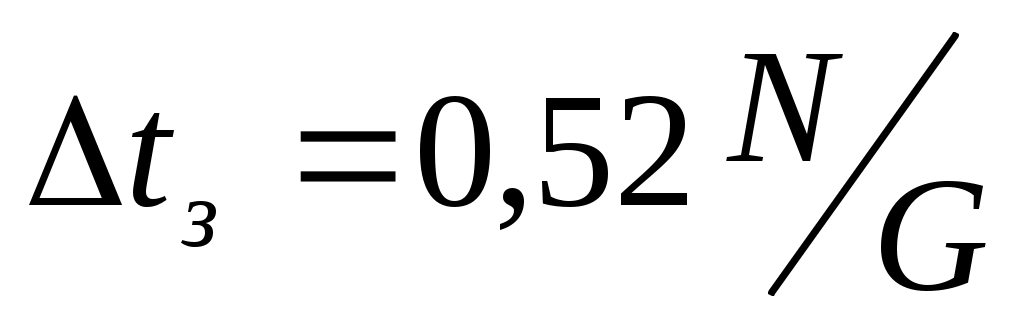 , (44)
, (44)
где N – в кВт; G – в кг/с.
Для зависимости
При выводе формул для kτи kагр средняя температура очистного агента считалась постоянной, точнее, медленно изменяющейся со временем (
Упрощенные зависимости для kτ
Для отдельных достаточно больших значений F0 формулы могут быть получены на основе общего выражения
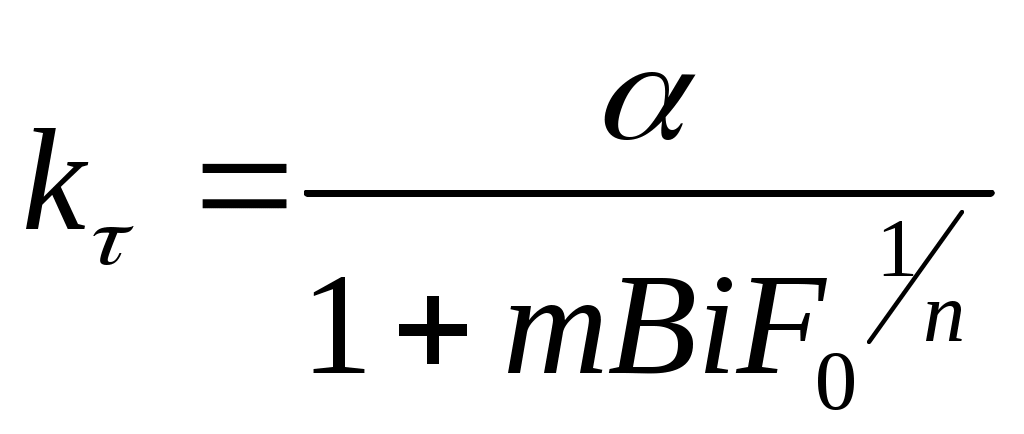 , (17а)
, (17а)где m>0, n≥1 (целое).
Для условий бурения скважин в большинстве случаев пригодна зависимость
При больших значениях Bi, характерных для условий бурения с промывкой водой и глинистыми растворами, можно использовать выражение
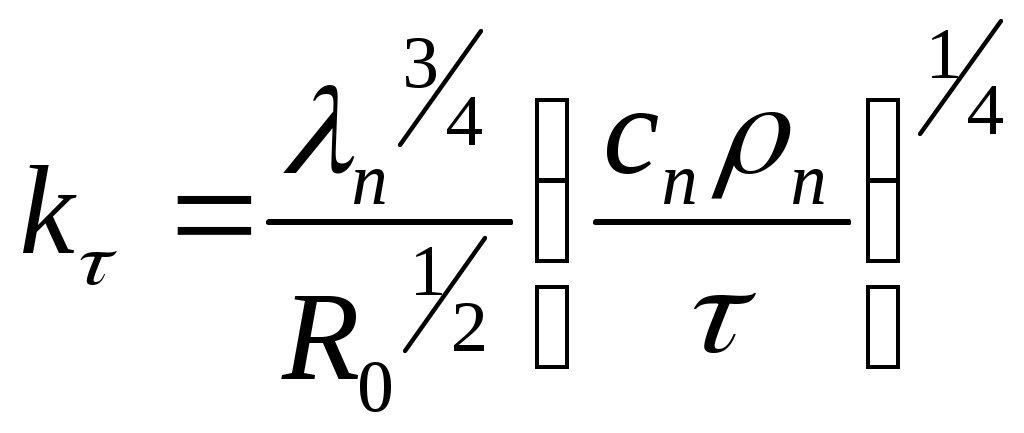 , (19)
, (19)где cп – удельная массовая теплоемкость породы, Дж/(кг·0C).
Среднеинтегральный по времени коэффициент нестационарного теплообмена можно получить из (18) с помощью теоремы о среднем
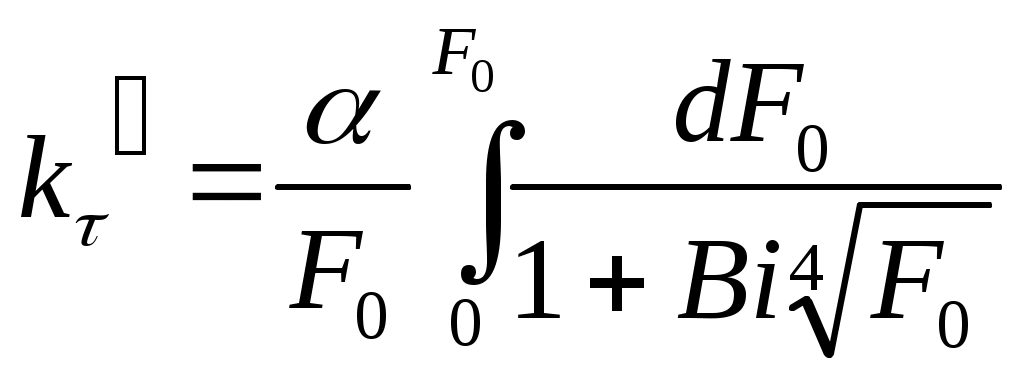 . (20)
. (20)Решением выражения (20) является
где
При бурении с промывкой водой и глинистыми растворами, при бурении с продувкой, когда b≥2, можно использовать простейшее выражение
Гидравлический уклон в бурильных трубах i1 и в кольцевом канале скважины i2 определяется из выражения
где p(требуют расчета!) – потери давления в соответствующем канале, Па; ρ – плотность очистного агента (для газа – при средних значениях температуры и давления в канале), кг/м3; H – глубина скважины, м.
Прирост температуры очистного агента за счет теплоты, генерируемой породоразрушающим инструментом
где N – мощность, реализуемая на забое, Вт.
Коэффициент теплопередачи через стенку бурильных труб, отнесенный к 1м труб
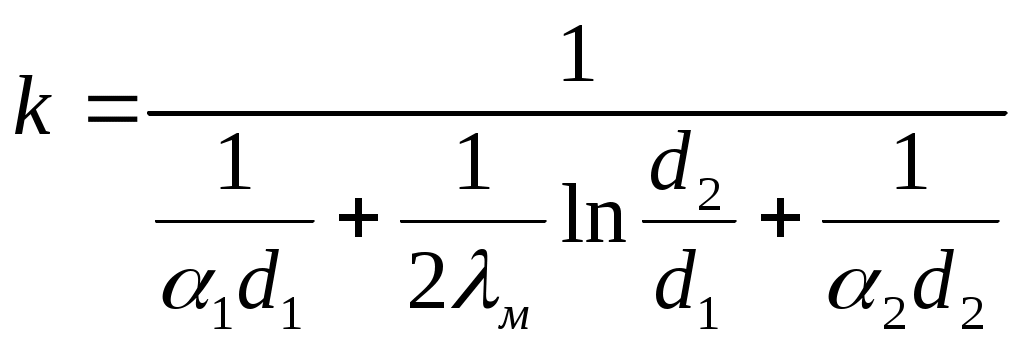 ,
, где d1, d2 – внутренний и наружный диаметры труб, м; α1, α2– коэффициенты теплоотдачи соответственно во внутреннем канале бурильных труб и в кольцевом канале скважины, Вт/(м2·0C); λм – коэффициент теплопроводности материала труб, Вт/(м·0C).
Для теплоизолированных труб используется аналогичная по структуре формула для многослойной цилиндрической стенки. Так, для труб, покрытых внутри слоем теплоизолятора
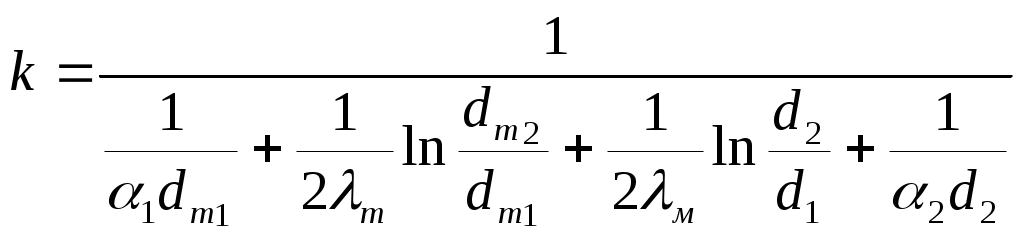 . (26)
. (26)Индекс “т” означает теплоизолирующий слой.
Коэффициент теплоотдачи α определяется через критерий Нуссельта Nu
где λ – коэффициент теплопроводности очистного агента, Вт/(м·0C).
При ламинарном течении ньютоновских сред (вода, воздух, солевые растворы)
,
где Pr – критерий Прандтля для очистного агента
где μ – коэффициент динамической вязкости очистного агента, Па·с; c – удельная массовая теплоемкость, Дж/(кг·0C).
При турбулентном течении ньютоновских сред
При бурении с продувкой воздухом можно использовать зависимость
Определение α при движении неньютоновских сред затруднено.
Для глинистого раствора в первом приближении можно пользоваться формулой академика Л.С. Лейбензона
где Re′ – обобщенный параметр Рейнольдса
В дальнейшем апостроф будем опускать.
При турбулентном течении глинистого раствора в трубах можно использовать формулу Б.И. Есьмана
В формуле (33) обобщенный параметр Прандтля определяется через µэф
Теплоотдача глинистого раствора при течении в кольцевых каналах изучена недостаточно. При турбулентном течении (Re≥10000) Ю.М. Проселков рекомендует формулу
При ламинарном течении глинистых растворов, в первом приближении, возможно использование зависимости (28) с заменой Re и Pr на Re′ и Pr′ (через µэф)/
Коэффициент kагр может быть определен по формуле Ю.Д. Дядькина
где ψ – удельная теплота плавления льда (кристаллизации воды), Дж/кг; Wп – активная массовая влажность породы (отношение массы льда или свободной воды в единице объема породы к ее объемной плотности), доли ед
.; [t] – абсолютное значение температуры очистного агента в кольцевом канале скважины, осредненное по протяженности расчетного участка и длительности циркуляции, 0C; kR – безразмерный коэффициент, зависящий от характера распределения температуры вокруг скважины.
Если принять kR=4,8 и ψ=3,34·105 Дж/кг, то
Тепло- и массообмен в призабойной зоне скважины
При работе породоразрушающего инструмента на забое выделяется теплота. По данным Л.А. Шрейнера физ. КПД разрушения пород составляет не более 0,01%, т.е., практически вся механическая энергия рассеивается в виде теплоты.
При установившемся режиме, когда породоразрушающий инструмент нагреется до постоянной температуры, количество теплоты, выделяющейся на забое в единицу времени, равно количеству теплоты, воспринимаемой очистным агентом.
Рисунок …
При бурении по “сухим” породам
При бурении с продувкой во влажных мерзлых породах теплота, генерируемая породоразрушающим инструментом, затрачивается на нагрев воздуха, шлама, плавление льда и испарение влаги.
Пренебрегая теплотой на нагрев шлама,
где Qм – количество теплоты, генерируемой инструментом, в единицу времени, Вт; Qпл, Qисп - количество теплоты, генерируемой инструментом, в единицу времени на плавление льда и испарение влаги, Вт.
При бурении с продувкой крайне желательно, чтобы вода не выделялась на забое в виде жидкой фазы (сальники), т.е., можно допустить плавление и испарение в единицу времени такого количества льда, которое могло бы довести воздух до 100-%-ной влажности. При движении воздуха к устью происходит его охлаждение и влага будет выпадать в виде инея и снега.
Поскольку насыщение воздуха до 100% возможно только за счет льда, количество теплоты на его плавление
и на испарение
, (41)
где ψ и ψ′ – скрытая теплота плавления льда и парообразования, Дж/кг; ΔW – температурный прирост влагосодержания воздуха, кг/(кг·0C).
Будем считать, что вся механическая работа на забое рассеивается в форме тепла (Qм=N). Подставим (40) и (41) в (39)
В случае бескернового бурения с большими механическими скоростями необходимо учитывать теплоту на нагрев шлама.
Для предупреждения растепления мерзлых пород сжатый воздух необходимо охлаждать. Влажность воздуха в призабойной зоне с большим запасом можно принять равной 10%.
При изменении относительной влажности воздуха от 10% до 100% в интервале температур –100C÷+100C, средний прирост его влагосодержания ΔW=0,00033 кг/(кг·0C). ψ=3,34·105 Дж/кг, ψ′=2,49·106 Дж/кг, cp=1·103 Дж/(кг·0C). Подставив эти значения в (43), получим приближенную формулу:
где N – в кВт; G – в кг/с.