Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 133
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
где
Если предположить, что при воздействии напряжения то в теле возникает мгновенная упругая деформация
Кривая текучести в данном случае есть прямая с углом наклона
где
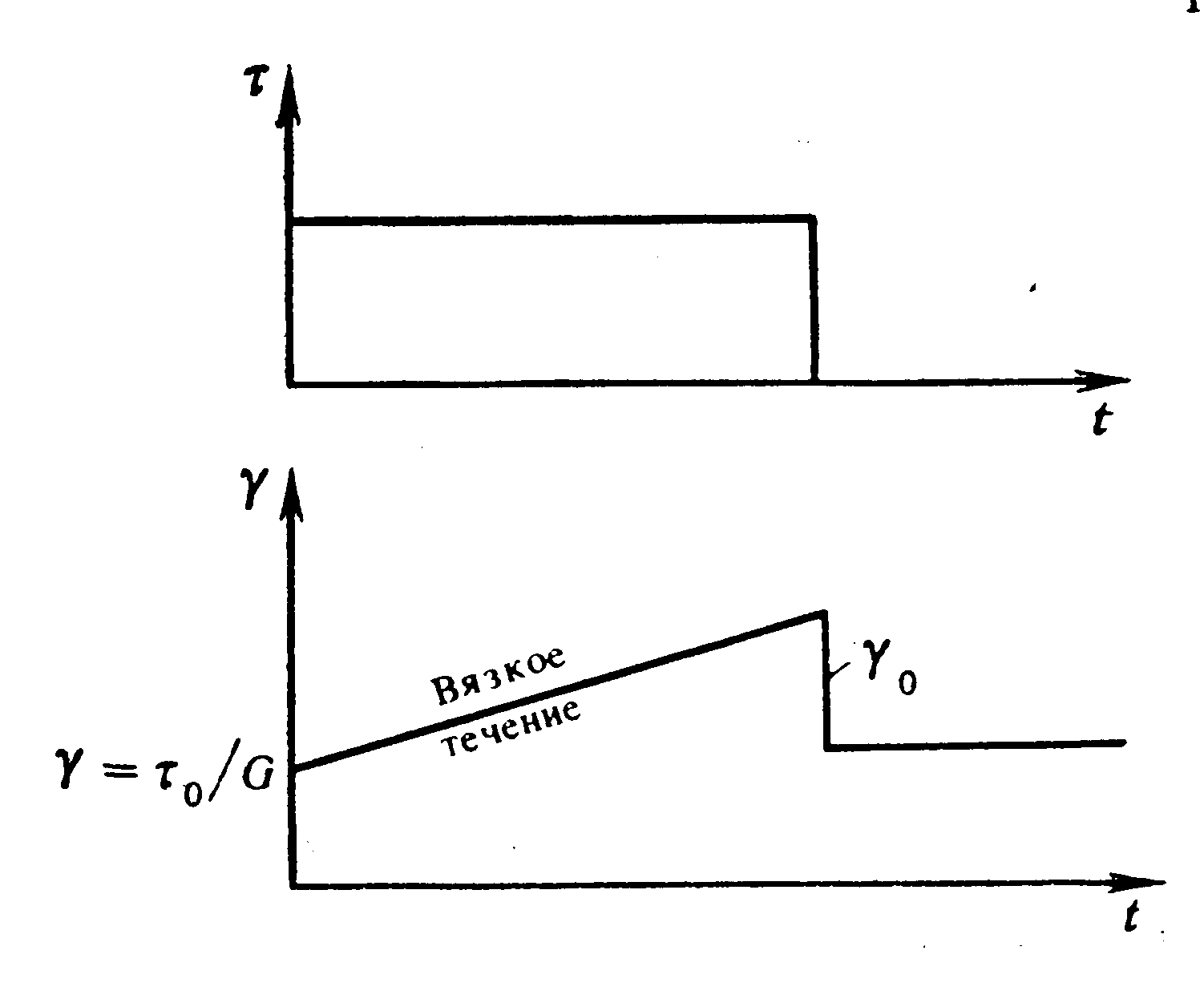
Рис. 2.6. Текучесть жидкости Максвелла
ДИАГРАММА РЭЛЕЯ
Ламинарная область (Re<1 – “ползущие движения” – капельки тумана, мельчайшая пыль в воздухе), где сопротивление среды пропорционально скорости в первой степени; хорошо описывается формулой С.Стокса.
В турбулентной области при Re>1000 сопротивление пропорционально квадрату скорости. С грубым приближением описывалось формулой Риттингера. В переходной области (Re=30200) приближенно справедлива формула А. Аллена.
В 30-е годы был разработан метод определения w0с помощью табличных или графических зависимостей между Re и безразмерным параметром Re2 (назван позднее параметром Лященко Li), в который w0 не входит:
В 1938г. П.В. Лященко предложил диаграмму:
Р
 ассчитывается Re2, по диаграмме определяют Re, затем рассчитывают критическую скорость:
ассчитывается Re2, по диаграмме определяют Re, затем рассчитывают критическую скорость:
правая часть (2), лишенная постоянного множителя
Точность определения w0 не выше 10%.
Решения задачи, выполненные Б.Б. Кудряшовым:
1.
2. Алгебраическое решение уравнения (5):
Справедлива в диапазоне Re=0,2÷105.
Максимальное отклонение +7,9% в точке Re=1.
Однако в науке в настоящее время принято пользоваться параметром Ar, поэтому (5) преобразовано к виду
а (6) – к виду
Максимальная ошибка около 6% при Re=105. Пригодна в диапазоне 1÷105.
Выражение (7) позволяет получить формулу критической скорости:
(справедлива в интервале Re=0,2÷105), а выражение (8) –
(в интервале Re=1÷105).
Влияние формы частиц.
Опытные данные (Б.Б. Кудряшов):
1
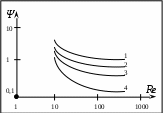 – пластинчатые;
– пластинчатые;2 – удлиненные;
3 – компактные;
4 – идеальные шары.
К величине скорости
надо добавить поправочный множитель
Значения kф можно считать постоянными только при Re≥500. При Re=500 для компактных kф=0,724, для удлиненной kф=0,606, для плоской kф=0,495.
Влияние стесненности движения.
1>
В стесненных условиях 0 всегда ниже, чем при свободном движении одной частицы в неограниченной среде.
2 вида стесненности:
-
стесненность канала -
стесненность совместного движения большого количества частиц.
Стесненность канала.
Определяется степенью стеснения, т.е. отношения площади миделевого сечения частицы (наибольшего сечения, перпендикулярного к направлению движения) к площади сечения канала. Для движения в круглых трубах это есть (dэ/Dэ)2- dэ – экв.диаметр частицы; Dэ – диаметр трубы.
Однако при бурении шлам обычно транспортируется в кольцевом канале.
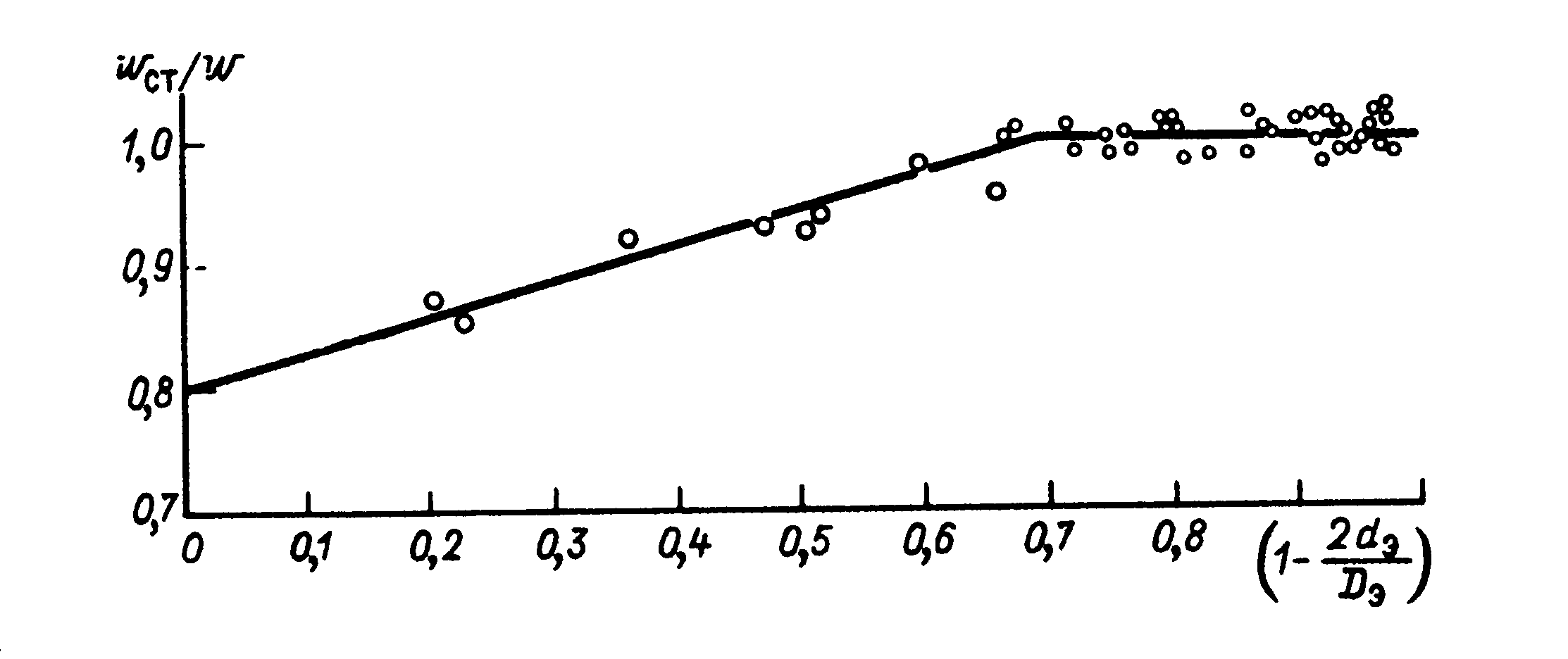
Опытные данные Б.Б. Кудряшова
Опытные точки и график зависимости относительной скорости равномерного падения стеклянных шариков в тяжелой жидкости от стесненности кольцевого канала
wст – критическая скорость стесненного падения
w – критическая скорость свободного падения
Коэффициент стесненности кольцевого канала
При
СТЕСНЕННОСТЬ СОВМЕСТНОГО ДВИЖЕНИЯ ЧАСТИЦ
Опытным путем выявлена основная закономерность сопротивления среды при стесненном движении частиц
т.е., сопротивление возрастает в степенной зависимости с уменьшением коэффициента разрыхления θ (отношение объема среды к общему объему двухфазной смеси).
Стесненное взвешивание частиц в восходящем потоке жидкости или газа описывается общей функциональной зависимостью между безразмерными параметрами
(2)
На основании изложенного ранее (ссылки!) можно записать
и, следовательно,
критическая скорость множества частиц
Величина
Зависимости (4) и (5) справедливы в диапазоне Re=0,2÷105.
При расчете критической скорости wст в формулу (5) подставляется эквивалентный диаметр частицы dэ и коэффициент формы kф в виде поправочного множителя. Средний показатель степени может быть принят как для шаров m=8.
Отношение критических скоростей при стесненном и свободном взвешивании
Из (6) следует вывод: если скорость восходящего потока среды становится равной или превышает критическую скорость в этой среде для одиночной частицы в свободных условиях, то явление стесненности совместного движения частиц теряет силу, т.е. скопление частиц полностью разрыхляется.
Свободное движение частиц в неньютоновской
(бингамовской) жидкости
Такие среды обладают предельным напряжением сдвига τ0.
Для шарообразной частицы, находящейся во взвешенном состоянии, движущая сила веса равна вертикальной составляющей напряжений на ее поверхности
откуда диаметр самой крупной частицы, остающейся во взвешенном состоянии
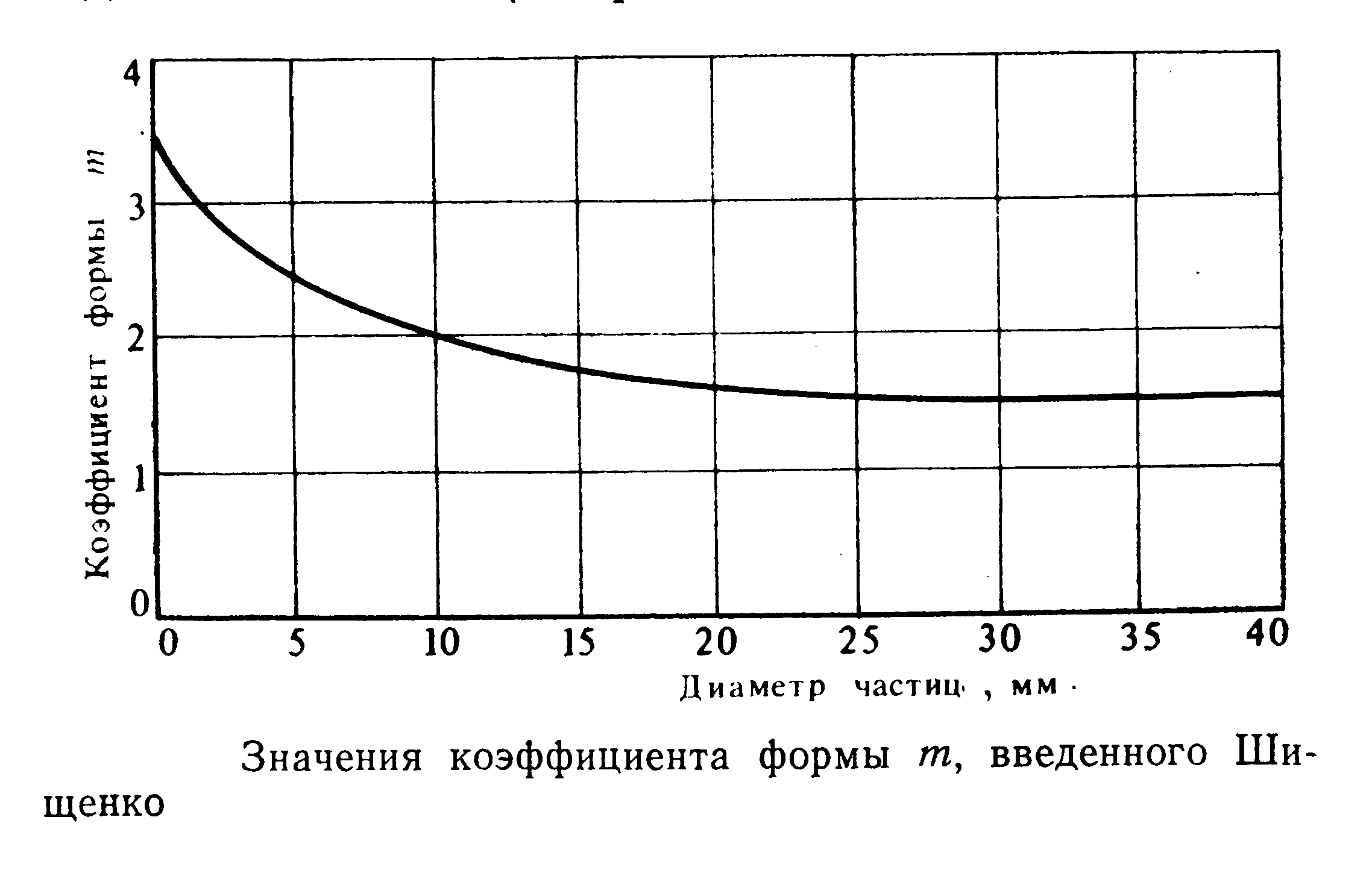
В действительности распределение касательных напряжений на поверхности шара неравномерно, поэтому Шищенко предложил применять экспериментальный коэффициент т, значение которого зависит от диаметра
Соотношение (9) можно использовать для оценки взвешивающей способности бурового раствора, оставленного в состоянии покоя. При циркуляции бурового раствора в скважине частицы, диаметр которых равен или меньше диаметра (9), выносятся на поверхность со скоростью движения бурового раствора. Внутри бессдвигового ядра течения увлекаемые частицы могут иметь больший диаметр, чем диаметр частицы в остальной части проходного сечения, поскольку величина
Для неподвижных тиксотропных жидкостей вместо τ0 следует использовать статическое напряжение сдвига θ (определяется на приборе СНС-2 при частоте вращения 0,2 об/мин).
Движение частиц в тиксотропных жидкостях весьма сложно, поскольку в определение Re надо вводить эффективную вязкость μэф в окрестности частицы.
τ и
Шищенко экспериментальным путем определил, что при a<3 режим обтекания ламинарный; при
В ламинарном режиме
где ψ(a) – экспериментальная функция
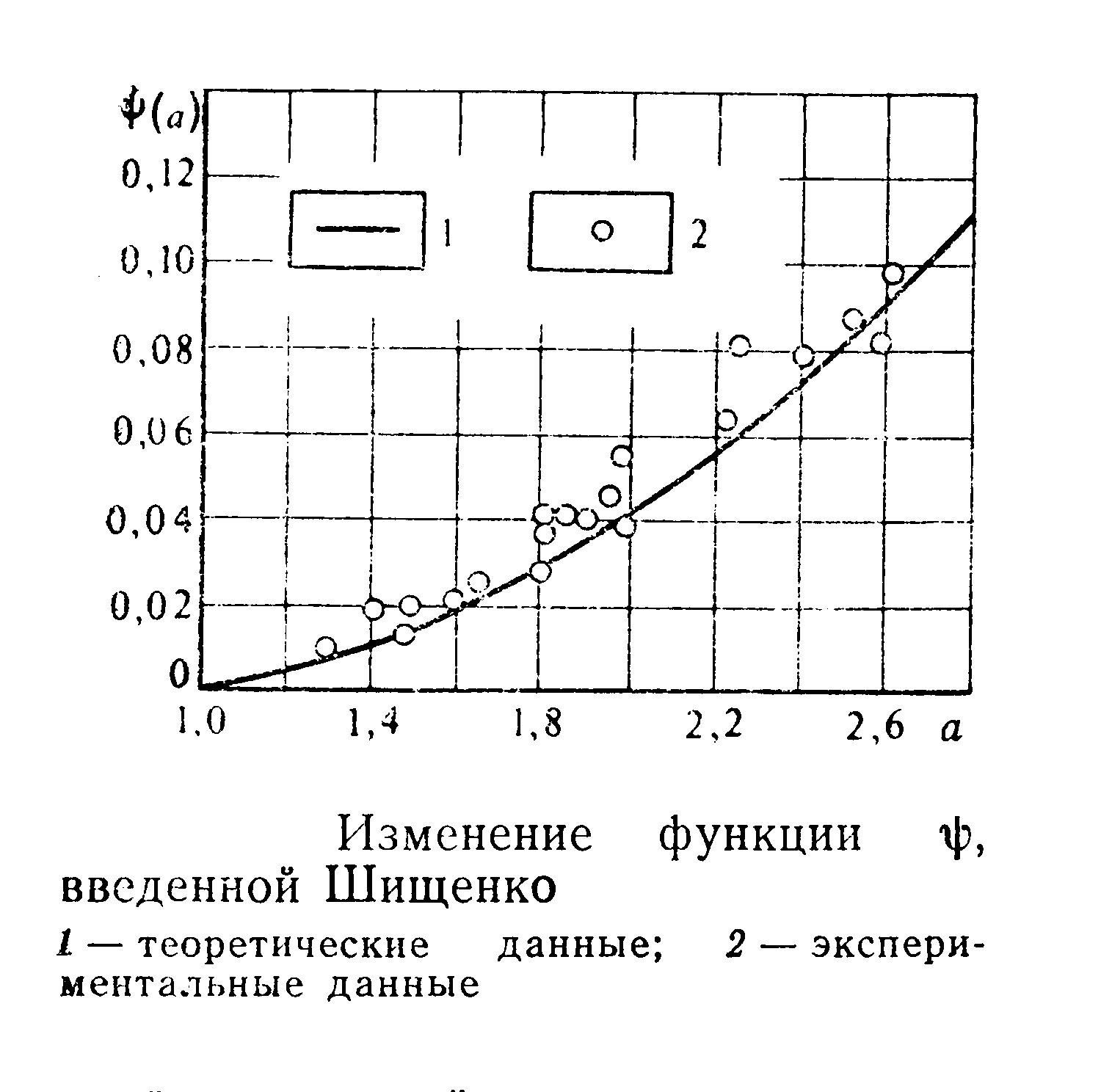
В переходном и турбулентном режимах w определяется по формуле Риттингера, в которой коэффициент сопротивления зависит от формы частицы и параметра a.
Значение коэффициента
ЛАМИНАРНОЕ ТЕЧЕНИЕ
Допущения: среда несжимаемая; движение установившееся, равномерное; течение параллельно оси трубы; среда прилипает к стенкам; труба имеет достаточную длину (нет концевых эффектов); единственные массовые силы – гравитационные.
-
Бингамовские жидкости.
Распределение скоростей в поперечном сечении потока . P – градиент давления, Па/м.
Уравнение (1) справедливо только в области, где