Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 136
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Предупреждение протаивания стенок скважины в мерзлых породах
Растепление породы с потерей связности ее частиц наступает, когда породе передано количество теплоты, достаточное для ее нагрева до 00C и для перехода льда-цемента в жидкое состояние. Предельно допустимым можно считать растепление, когда порода только нагрелась до 00C.
Количество теплоты, переданной от очистного агента стенкам скважины на единицу длины ствола в единицу времени
где t – температура очистного агента; Tст – температура стенки скважины.
Для такого же количества теплоты, переданной в единицу времени мерзлым породам, не затронутым растеплением, справедливо выражение
где Tп – естественная температура пород.
Приравняем (45) и (46), приняв Tст=00C и обозначив температуру среды как tmax:
Формула (47) позволяет определить максимально допустимую температуру очистного агента, при которой температура стенок скважины за период циркуляции достигнет 00C, т.е., растепления мерзлых пород не произойдет.
Если в (47) вместо kτ подставить его приближенное значение (19) и раскрыть значения Bi и F0, то
При жидкостной промывке, особенно при турбулентном режиме течения, даже при кратковременной циркуляции жидкости с положительной температурой происходит оттаивание мерзлых пород. При малых значениях Bi (бурение с продувкой, промывкой пеной) допустима небольшая положительная температура очистного агента. Однако, возможно поверхностное растепление пород, слипание шлама (при продувке), образование сальников.
Полная гарантия от растепления – tmax<00C.
Влияние скважины на температурное и агрегатное состояние окружающего массива
Из определения kτ (для случая охлаждения массива) при R=R0
где T – температура пород на расстоянии R от оси скважины; Tп – естественная температура горных пород.
Положим, что величина
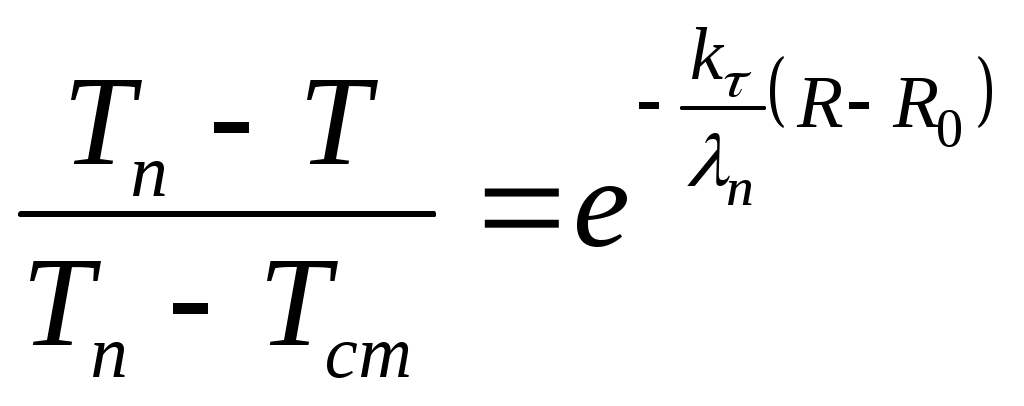 , (50)
, (50)где Tст – температура стенки скважины в данный момент времени.
Количество теплоты, переданной от массива к очистному агенту на единице длины скважины в единицу времени
и
Приравняем (51) и (52), найдем выражение для Tст из (50) и получим формулу для распределения температуры в массиве вокруг скважины
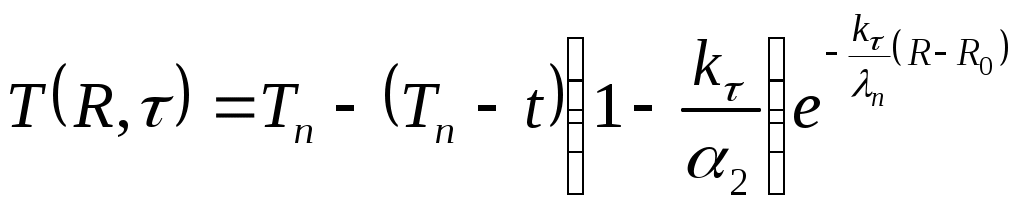 (53)
(53)Если температура очистного агента медленно изменяется во времени, то вместо kτ следует подставлять kτ′.
Зона изменения агрегатного состояния массива вокруг скважины
В (53) положим R=Rагр, T(R, τ)=00C и подставим вместо kτ произведение kагр·kτ. Тогда радиус зоны изменения агрегатного состояния пород при постоянной температуре очистного агента
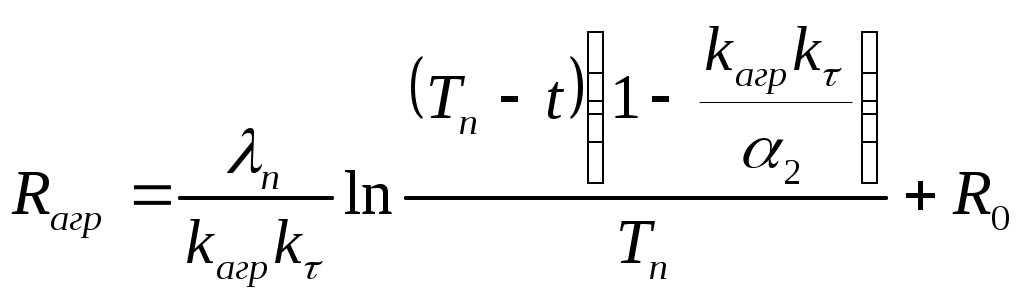 (54)
(54)Можно получить и более простое выражение.
Рассмотрим случай протаивания окружающих скважину мерзлых пород при постоянной температуре очистного агента t.
Общее количество теплоты, переданное от очистного агента к массиву за определенный период времени в условиях изменения агрегатного состояния пород
откуда
Теплота, затраченная на изменение температуры пород на единице длины скважины за определенный период времени
Общее количество теплоты с учетом части теплоты, затраченной на таяние льда в массиве на единице длины скважины за тот же период времени τ
Подставим (57) и (58) в (56):
Количество теплоты на изменение агрегатного состояния пород можно также выразить как
где Wп - активная массовая влажность (льдистость) породы, доли ед.
Приравняв (59) и (60), получим
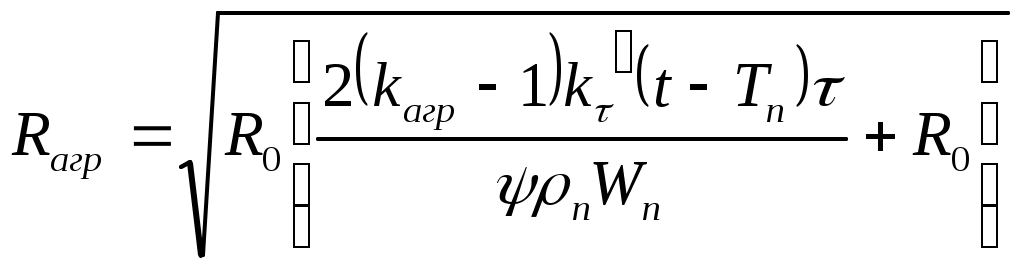 . (61)
. (61)Аналогично выводится формула для расчета радиуса замораживания влажных пород с положительной температурой при циркуляции хладоносителя
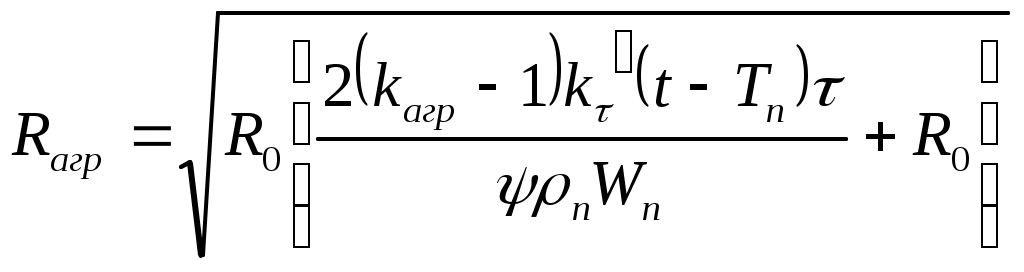 (61)
(61)Зона теплового влияния скважины на окружающий массив
Под зоной теплового влияния скважины понимают область, в которой температура пород отличается от естественной Tп.
Теоретически тепловой поток распространяется до бесконечности, но всегда существует зона, на границе которой температура пород практически не отличается от Tп.
Количество теплоты на изменение температуры пород выражается формулой (57). Поскольку вся эта теплота затрачивается на образование зоны теплового влияния, то
где Rп – радиус теплового влияния; Tп.ср – средняя температура пород в зоне теплового влияния; cп – удельная теплоемкость породы (средняя для мерзлой и немерзлой зон).
Tп.ср надо определять как среднее между средним по времени τ значением температуры стенки Tст′ и Tп;
Для всего количества теплоты, поступившей в массив, справедливо выражение (58), а также
Приравняем (58) и (64):
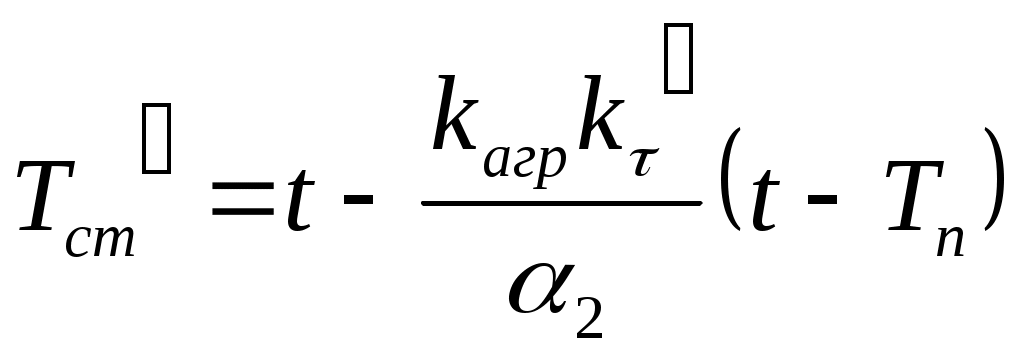 (65)
(65)Подставим (65) в (63):
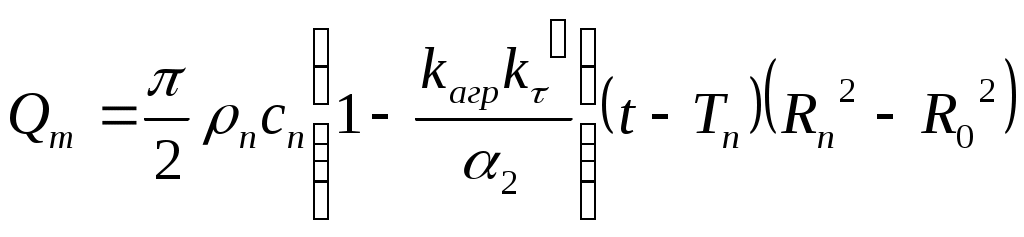 (66)
(66)Приравняем (57) и (66) и найдем Rп.
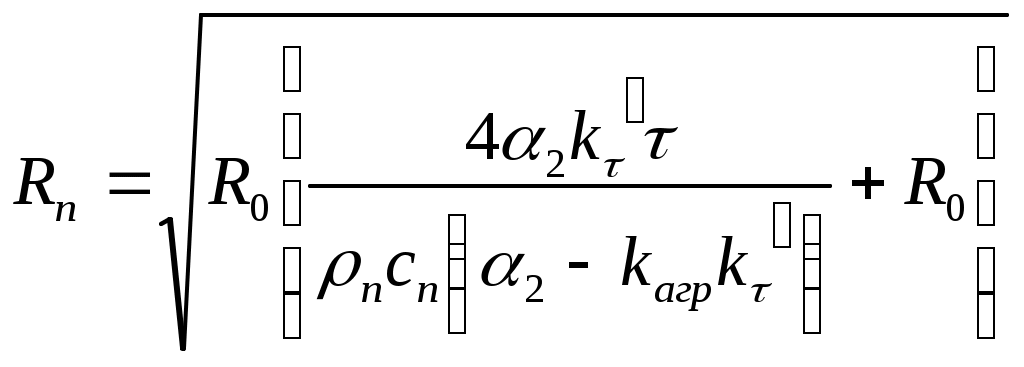 (67)
(67)Температурное поле в массиве вокруг скважины
Помимо формулы (53) можно получить и простые зависимости для радиального распределения температуры в массиве, в том числе, с учетом агрегатного перехода влаги.
Если рассматривать теплообмен в каждый отдельный момент времени как квазистационарный, то для теплового потока от очистного агента в массив через цилиндрическую стенку элементарной толщины dR на расстоянии R от оси скважины
Из (68) получаем выражение для мгновенного радиального распределения температуры в теле цилиндрической стенки переменной во времени толщины
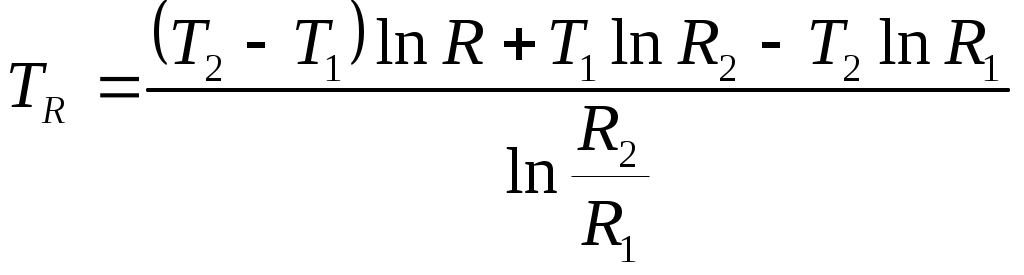 (69)
(69)Индексы 1 и 2 относятся соответственно к внутренней и наружной поверхностям цилиндрической стенки.
Рассмотрим тепловое влияние скважины на окружающий мерзлый массив без изменения агрегатного состояния пород при их нагреве. Температуру стенки скважины в определенный момент времени τ можно получить, приравняв формулы (45) и (46):
Подставив в формулу (69) R=R0, R2=Rп, T1=Tст, T2=Tп, с учетом (70), получим формулу для распределения температуры в зоне теплового влияния скважины в любой момент времени τ от начала процесса теплообмена при отсутствии фазовых переходов влаги
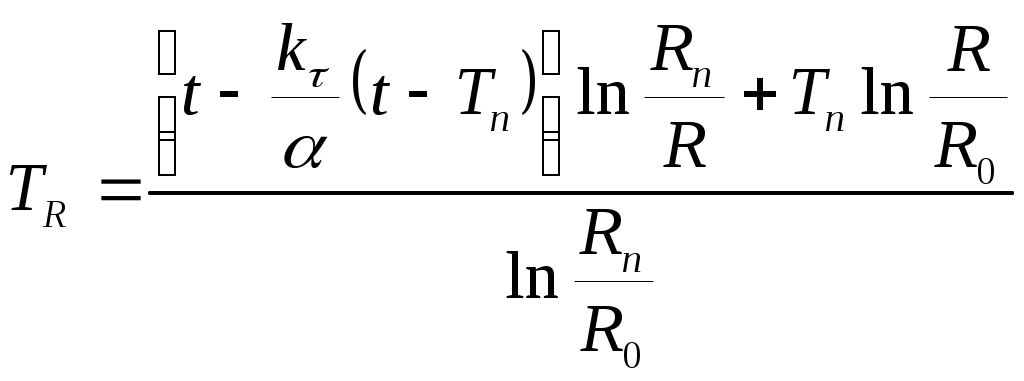 . (71)
. (71)Формула (71) справедлива при R0≤R≤Rп.
При изменении агрегатного состояния влаги распределение температуры в зоне изменения агрегатного состояния и за ее пределами описывается двумя разными формулами.
Температура стенки скважины в любой момент времени τ по аналогии с (70)
Подставив в (69) R1=R0, R2=Rагр, T1=Tст(с учетом (72)), T2=Tагр=00C, получим формулу для радиального распределения температуры в зоне изменения агрегатного состояния в любой момент времени τ
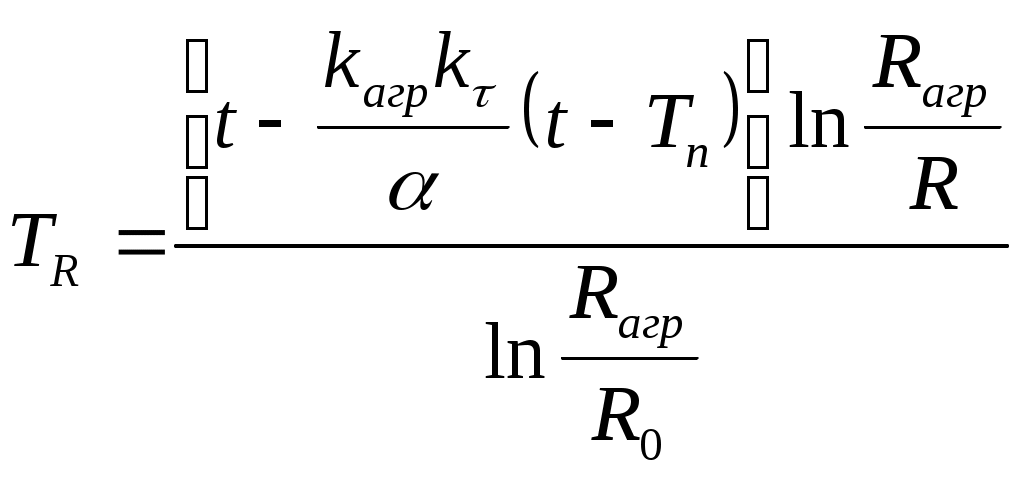 (73)
(73)Формула справедлива при R0≤R≤Rагр.
Подставив в (69) R1=Rагр, R2=Rп, T1=Tагр=00C, T2=Tп, получим формулу для радиального распределения температуры за пределами зоны изменения агрегатного состояния влаги
Формула справедлива при Rагр≤R≤Rп.
При вычислениях TR=f(R) для определенного момента времени τ по формулам (71), (73) и (74) необходимо знать среднюю температуру очистного агента t на расчетном участке, естественную температуру пород Tп, вычислить kагр по формуле () и определить kτ, kτ′, RагриRп для этого же момента времени τ по формулам
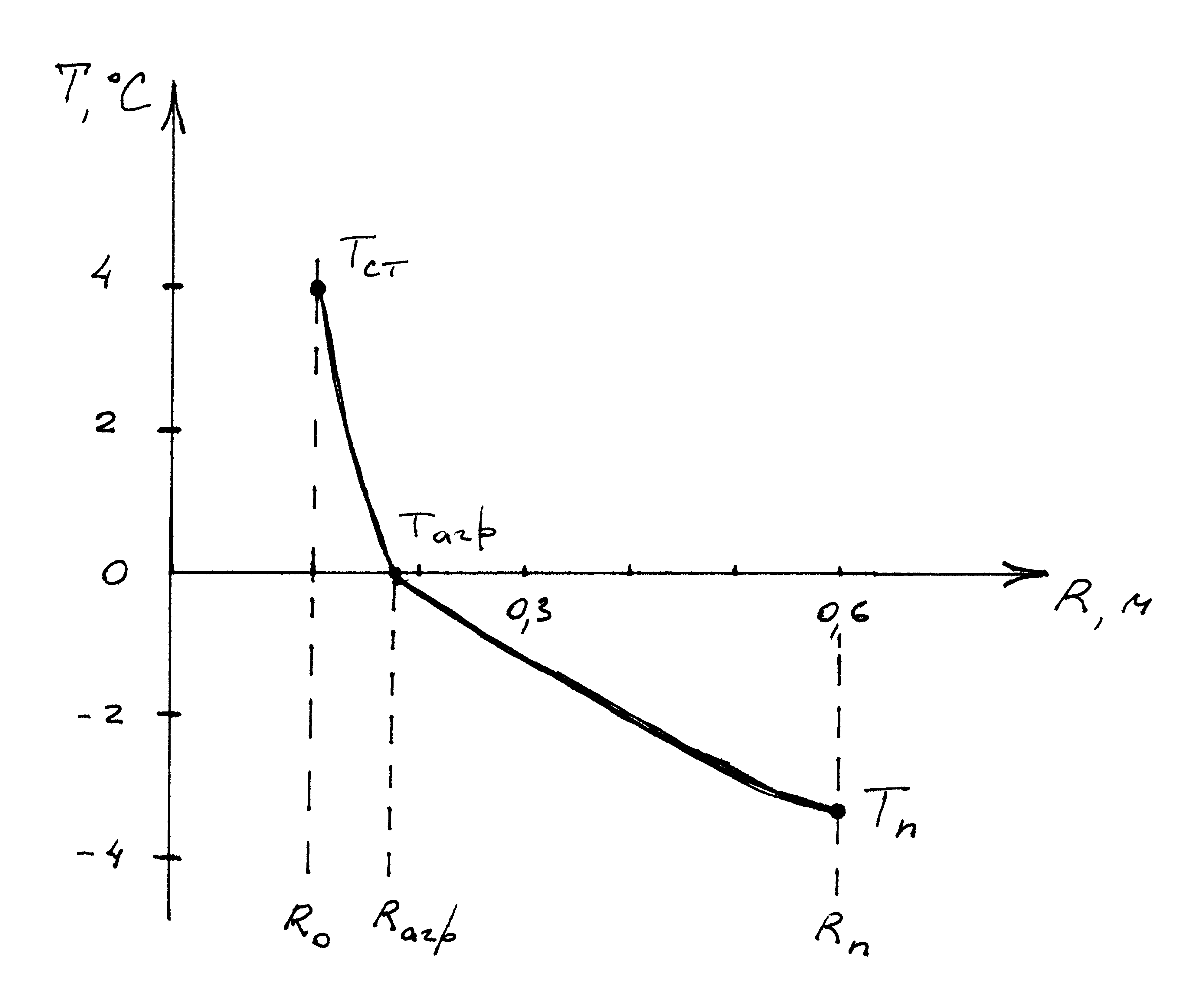
Распределение температуры: продувка воздухом t=200C, Tп=-30C, R0=0,1м; τ=8ч.
Температурный режим скважины при бурении с продувкой воздухом
Применительно к колонковому бурению в мерзлых породах при небольшой глубине скважины в основных зависимостях для расчета температуры очистного агента в бурильной колонне и кольцевом канале скважины без большой ошибки можно принять σ=0; i1=i2=0;
В бурильных трубах