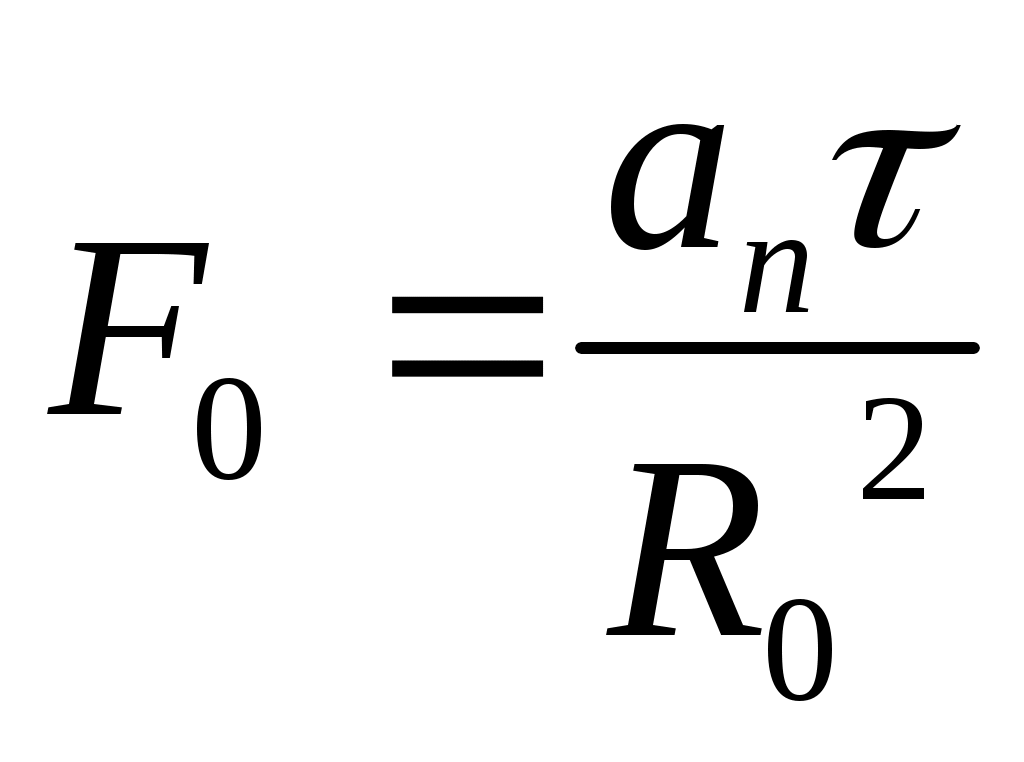Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 141
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– Блесса
Циркул. систему разбивают на участки с одинаковыми геометрическими характеристиками канала: 1). кольцевой зазор между БК и обсадной колонной; 2). кольцевой зазор между БК и стенками скважины; 3). кольцевой зазор между УБТ и стенками скважины; 4). внутренний канал УБТ; 5). внутренний канал БК.
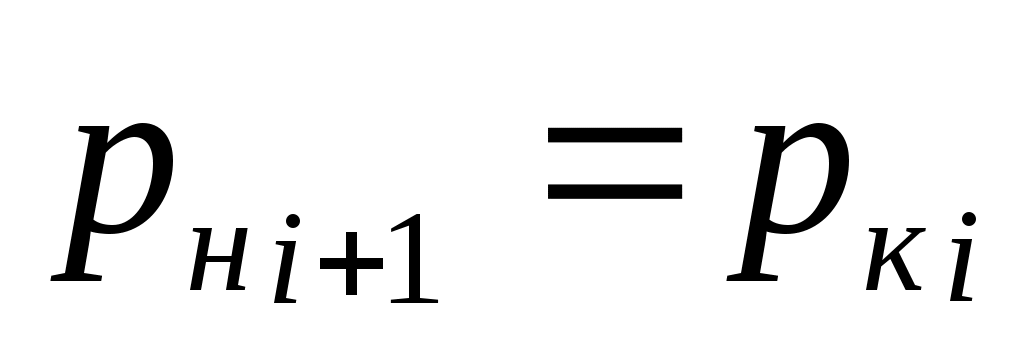
На забое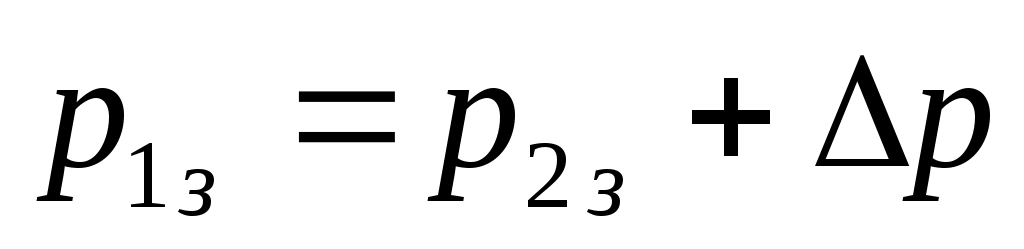
ТЕМПЕРАТУРНЫЙ РЕЖИМ СКВАЖИН
Важность:
Температурный режим – распределение температуры циркулирующего очистного агента во внутреннем канале БК и в кольцевом канале скважины.
Нисходящий поток (в буровых трубах) находится в состоянии теплообмена с восходящим потоком в кольцевом канале, который изменяет свою температуру также и за счет теплообмена с породами.
Процесс теплообмена нестационарный, зависит от продолжительности циркуляции.
В призабойной зоне очистной агент нагревается за счет теплоты, генерируемой породоразрушающим инструментом.
Энергия, затрачиваемая на преодоление гидравлических (или аэродинамических) сопротивлений, рассеивается в виде теплоты (диссипация энергии), что также оказывает влияние на температурный режим. Самостоятельным источником теплоты является трение буровых труб о стенки скважины.
При бурении с продувкой происходят также процессы массообмена (изменение влажности воздуха или газа), что существенно влияет на температуру.
При бурении в многолетнемерзлых породах теплообменные процессы осложняются изменениями фазового состояния влаги в породах, что сильно влияет на направление и интенсивность тепловых потоков.
Основные факторы, влияющие на температурный режим:
1). расход и начальная температура очистного агента;
2). скорость течения и турбулентность потоков;
3). физические и теплофизические свойства очистного агента и горных пород;
4). естественная температура пород и характер ее изменения по глубине;
5). конструкция БК и свойства материала;
6). скорость бурения и продолжительность рейса;
7). мощность, генерируемая породоразрушающим инструментом;
8). фазовые превращения влаги в горных породах и др.
Решение, полученное Б.Б. Кудряшовым в 1964 г.
Рассмотрим бурение скважины в мерзлых породах при прямой циркуляции очистного агента.
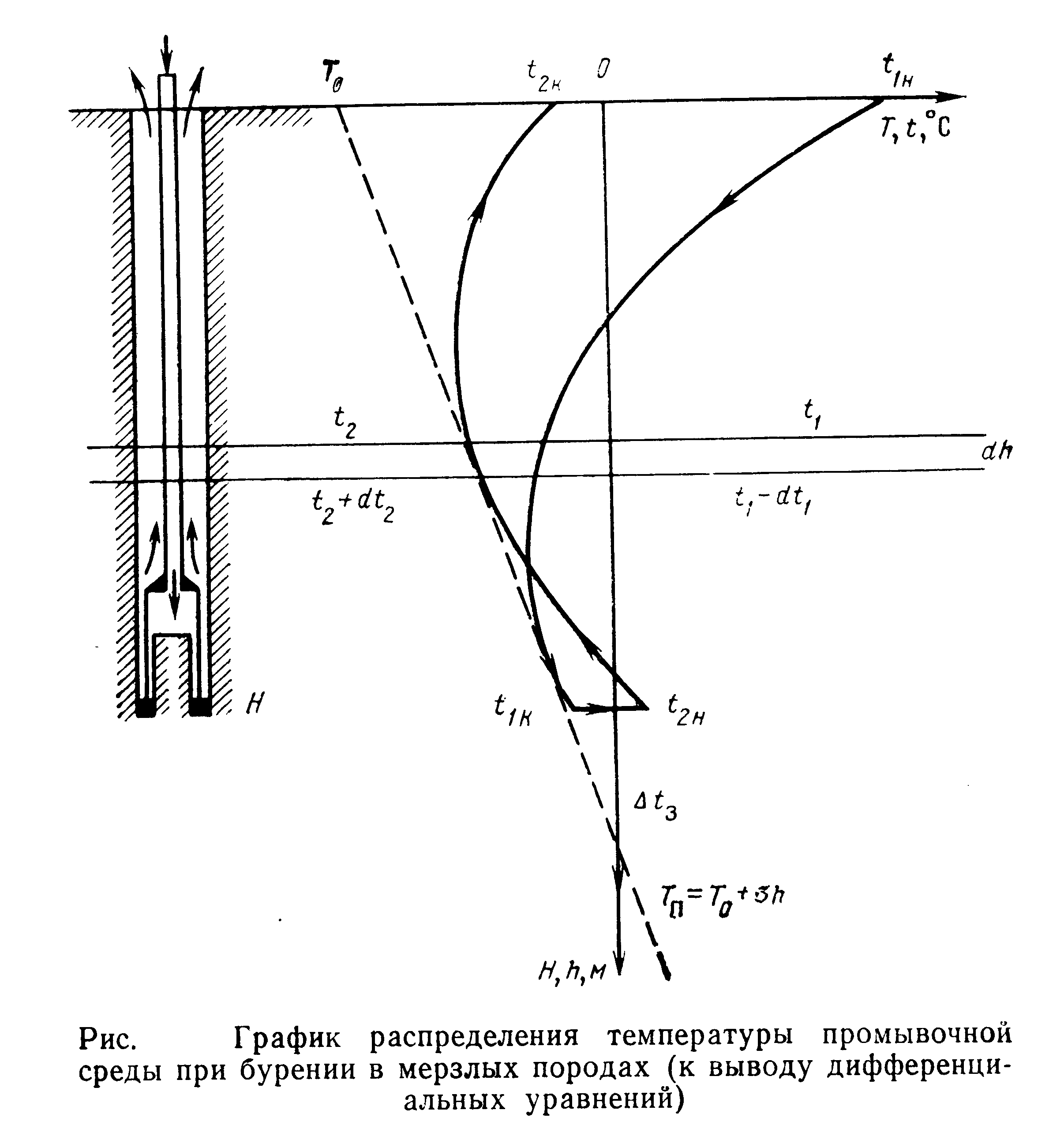
Очистной агент нагнетается в БК с начальной температурой t1н. При движении вниз он охлаждается в результате теплообмена через стенку буровых труб с более холодным очистным агентом. В зоне забоя очистной агент нагревается на Δtз за счет теплоты, генерируемой породоразрушающим инструментом.
При течении вверх по кольцевому каналу очистной агент охлаждается за счет теплообмена с мерзлым массивом. Начиная с некоторой глубины, начинается нагрев в результате интенсификации теплообмена с теплым нисходящим потоком.
Для составления дифференциальных уравнений теплообмена примем допущения:
1). естественная температура пород возрастает с глубиной прямолинейно;
2). физические и теплофизические свойства очистного агента постоянны, а их величины принимаются при средних значениях t и p.
3). физические и теплофизические свойства горных пород по глубине скважины постоянны;
4). коэффициент нестационарного теплообмена kτ между очистным агентом и массивом пород зависит от продолжительности циркуляции (рейса бурения) и не зависит от изменяющейся во времени температуры очистного агента;
5). влияние фазовых переходов влаги, содержащейся в породах, на температурный режим скважины, вызывает интенсификацию теплообмена, которая может быть учтена с помощью коэффициента интенсификации теплообмена kагр;
6). при бурении с продувкой влияние массообмена (изменения влагосодержания воздуха) на температурный режим учитывается только в призабойной зоне.
Допущения 1, 2 и 3 общеприняты для аналитического решения задачи.
4: точное аналитическое решение для коэффициента kτ получено при условии постоянства температуры очистного агента. В действительности температура изменяется с течением времени. Погрешность может быть устранена применением среднеинтегрального по времени значения kτ".
В процессе непрерывного теплообмена kτмонотонно снижается и его среднее значение всегда больше конечного. Из-за прерывности процесса бурения при его возобновлении даже после длительного простоя мы имеем дело с массивом пород, затронутых тепловым влиянием очистного агента, т.е.
tст≠tп.ест..
Поэтому значение kτ″ должно быть ниже среднего за период непрерывной циркуляции (рейс).
Пренебрежение изменением температуры очистного агента в течение рейса и недоучет теплового влияния предыдущих рейсов в некоторой мере компенсируют друг друга.
5 – практически единственная возможность решения задачи в условиях изменения фазового состояния влаги в породах.
6 – для бурения с продувкой в мерзлоте воздух целесообразно охлаждать до отрицательных температур и осушать, поэтому его влажность при теплообмене с мерзлыми породами может только возрастать. Возможный прирост температуры при этом несколько снижается.
Выделим элементарный участок dh в части скважины, где очистной агент в направлении своего течения только охлаждается. Тогда нисходящий поток в единицу времени с учетом выделения теплоты за счет работы сил трения потока теряет количество теплоты
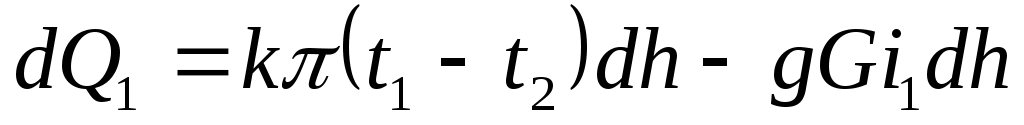 (1)
(1)
Количество теплоты, потерянной восходящим потоком
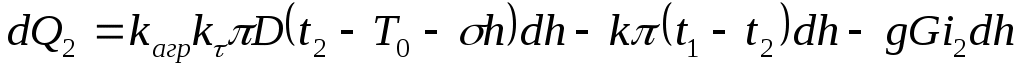 (2)
(2)
При этом температура в нисходящем потоке с глубиной уменьшится, в восходящем – возрастет =>
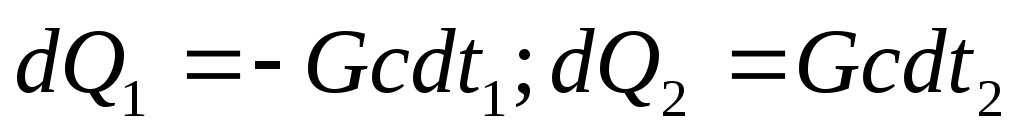 .
.
Подставим эти выражения в (1) и (2):
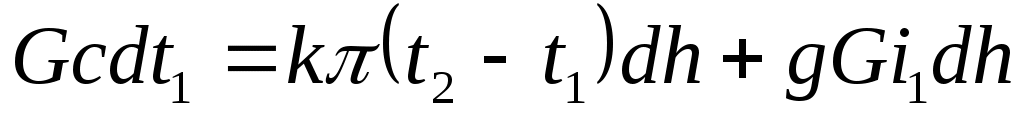 (3)
(3)
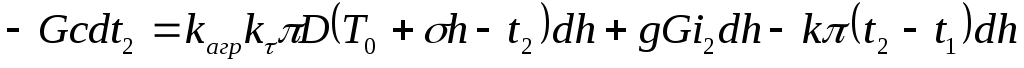 (4)
(4)
t– температура очистного агента,0C; T0– температура пород у поверхности,0C; h– глубина (текущая координата), м;G– массовый расход очистного агента, кг/с; c– удельная теплоемкость очистного агента, Дж/(кг·0C); D– диаметр скважины, м;k– коэффициент теплопередачи через стенку бурильной трубы, отнесенный к 1м трубы;g=9,81 м/с2;kагр– безразмерный коэффициент интенсификации теплообмена при изменении агрегатного состояния пород;kτ– коэффициент нестационарного (зависящего от времени) теплообмена между очистным агентом и горной породой, Вт/(м2·0C);i– гидравлический уклон (безразмерная величина);σ– геотермический градиент, 0C/м.
Индекс “1” – внутренний канал БТ,
“2” – кольцевой канал скважины. Индексы “н” и “к” – начальное и конечное состояние в соответствующем канале.
Поделим (3) и (4) на Gc и dh:
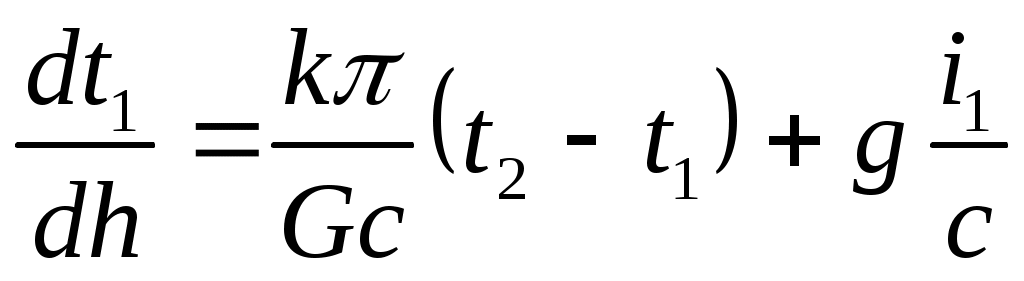 (5)
(5)
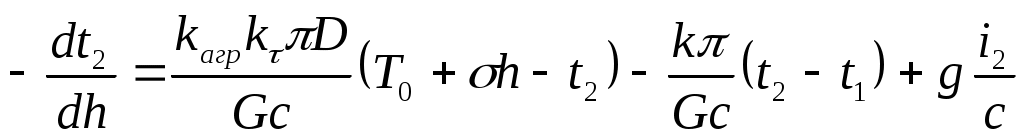 (6)
(6)
С помощью уравнения (5) выразим t2 и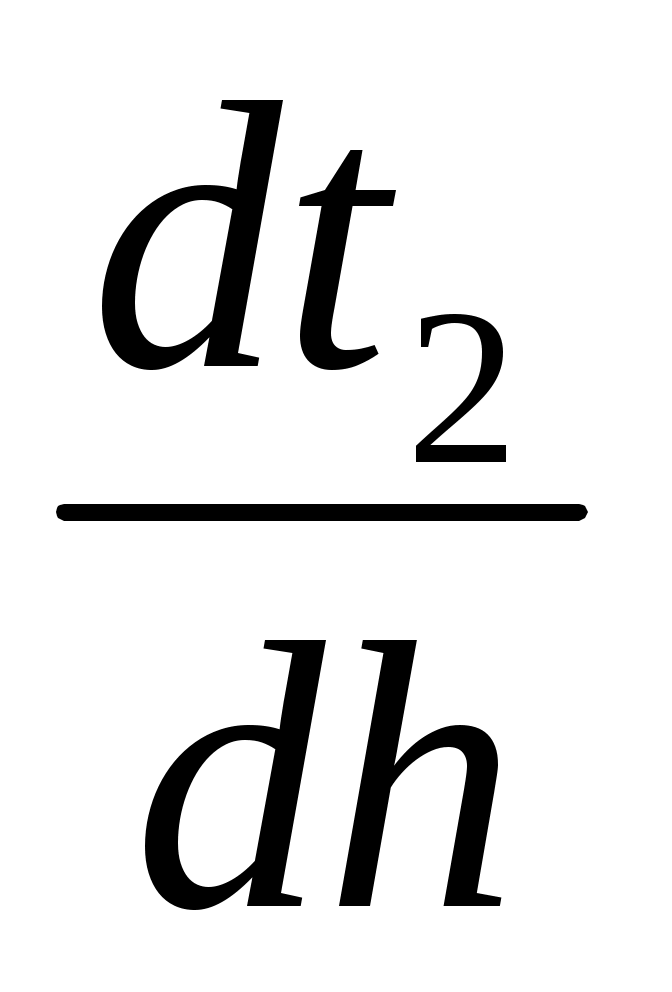 через t1:
через t1:
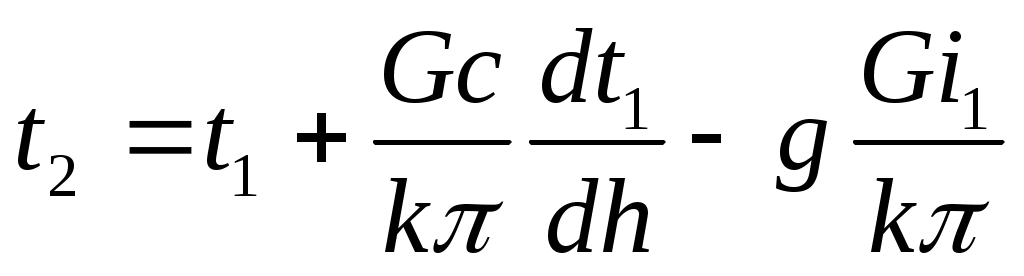 (7)
(7)
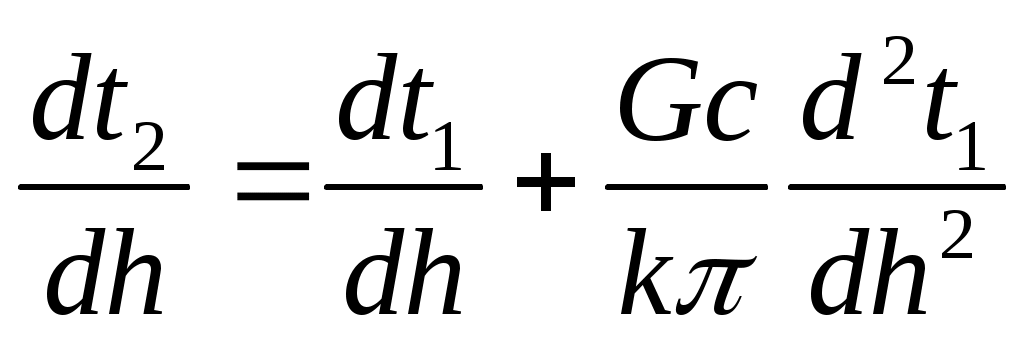 (8)
(8)
Для установления связи только между t1 и h подставим выражения (7) и (8) в (5) и (6) и, после преобразований, получим
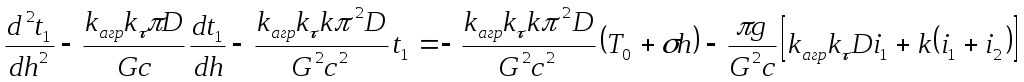 (9)
(9)
Получили неоднородное (с правой частью) линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Общее решение уравнения (9) имеет вид:
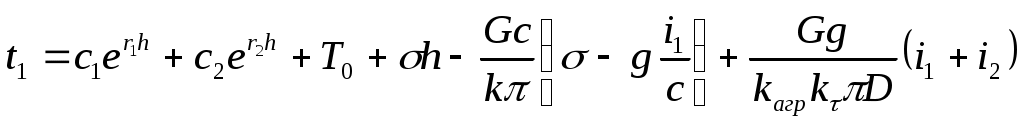 , (10)
, (10)
где c1 и c2 – постоянные интегрирования; r1 и r2 – корни характеристического уравнения
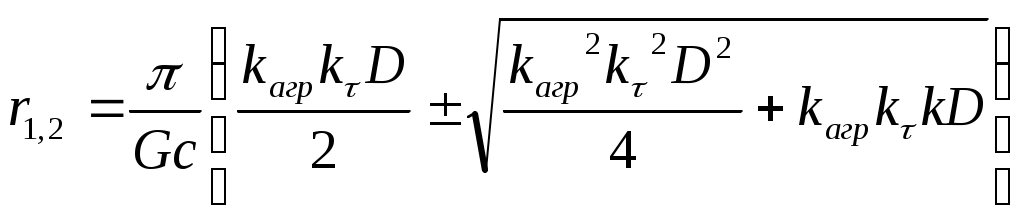 (11)
(11)
Постоянные интегрирования определяются из граничных условий:
1. при h=0 t1=t1н, например, t1=150C.
2. в реальных условиях очистной агент на забое воспринимает теплоту, генерируемую породоразрушающим инструментом => на забое
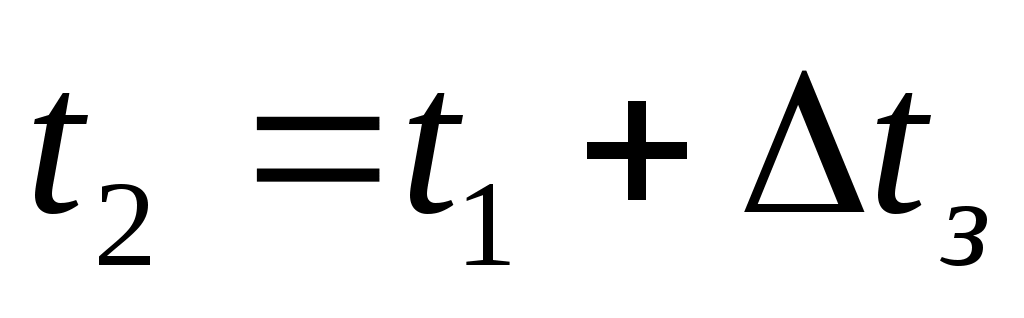 (12)
(12)
Наряду с этим на забое и на любой глубине h должно соблюдаться условие (7), получим
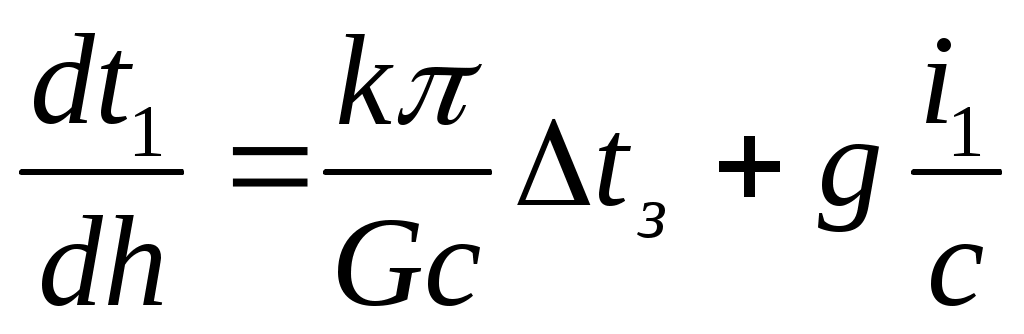 (13)
(13)
Это второе граничное условие для нисходящего потока.
Итак, имеем 2 граничных условия:
при h=0 t1=t1н;
при h=H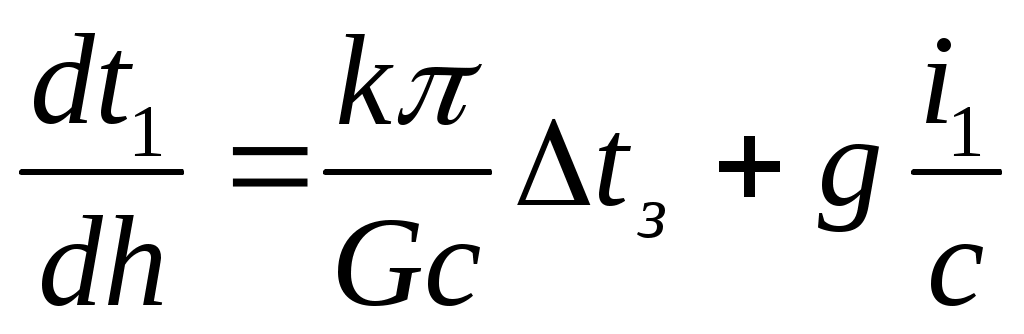 .
.
На их основании из общего решения (10) получим
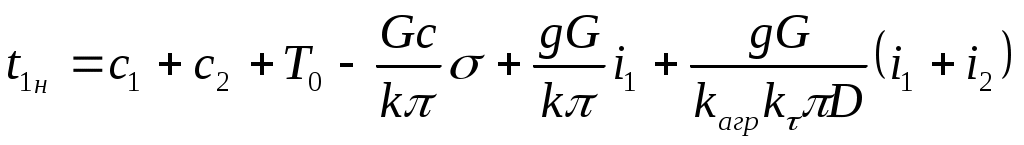 (14)
(14)
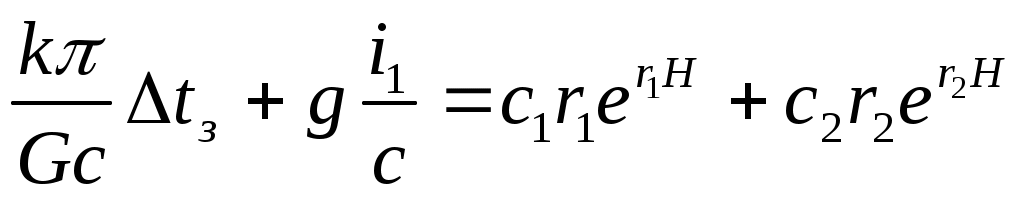 , (15)
, (15)
где H– глубина скважины, м.
Совместное решение (14) и (15) позволяет найти c1 и c2. Подставим их в общее решение (10). Температура в нисходящем потоке на любой глубине h
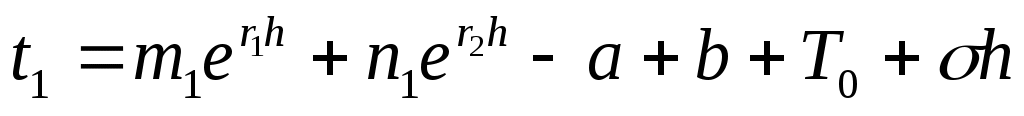 , (16)
, (16)
где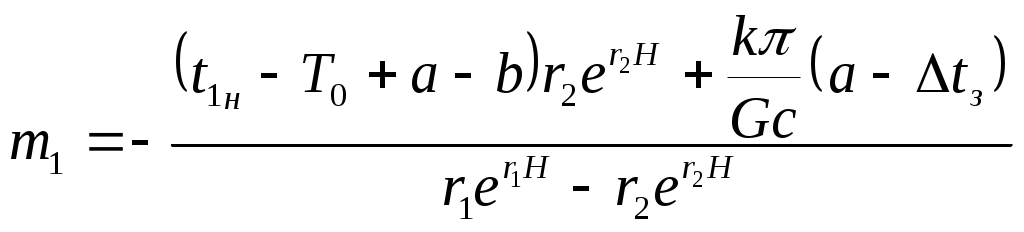 ;
;
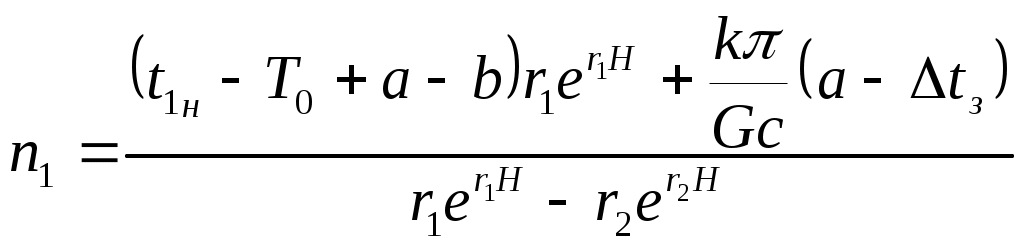 ;
;
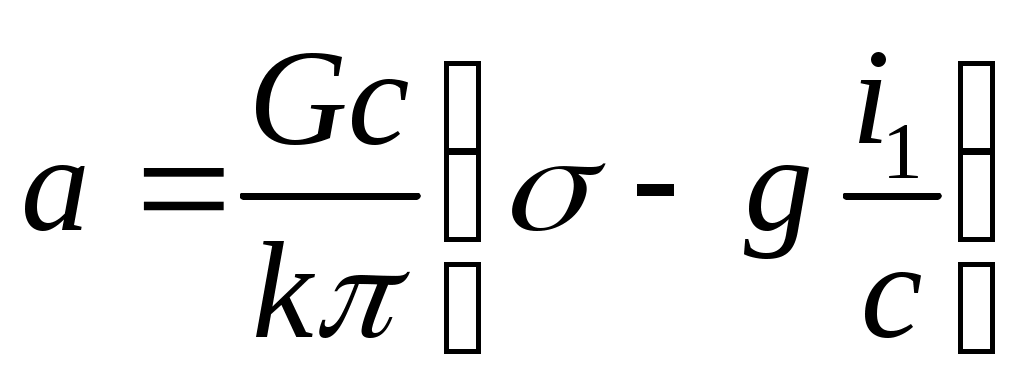 ;
; 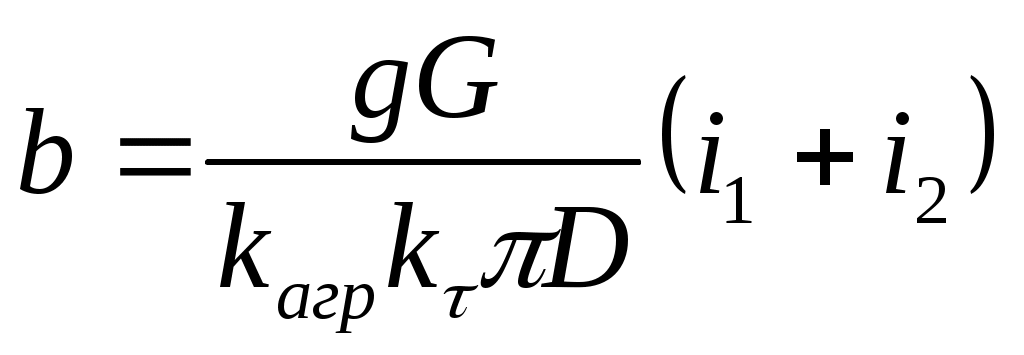 .
.
С помощью выражения (7) можно получить формулу для расчета t2.
С учетом того, что
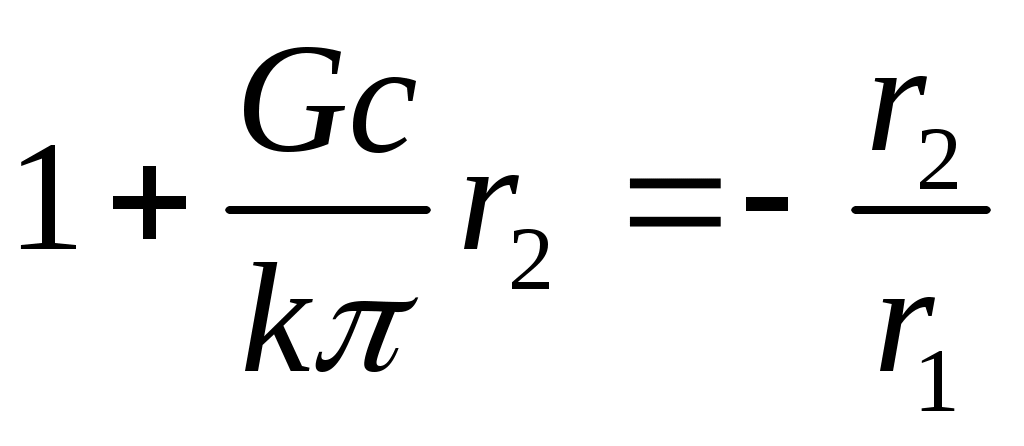 и
и 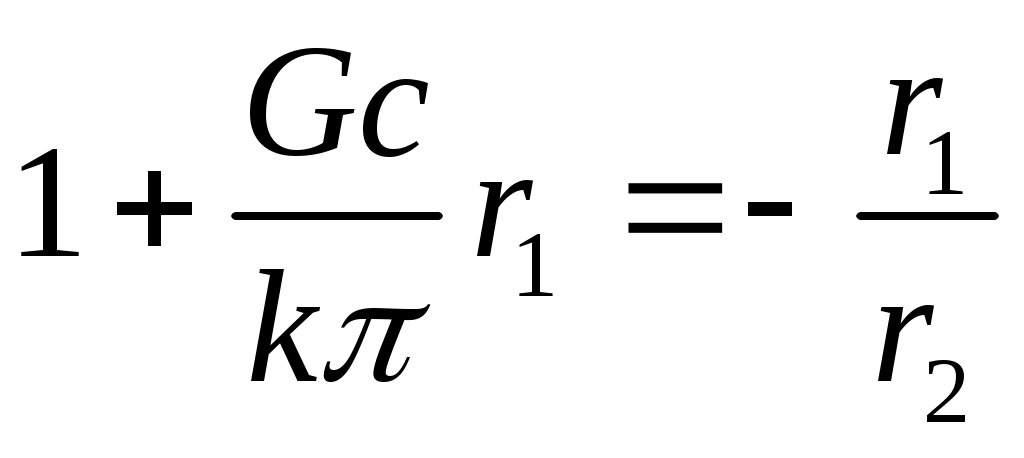 ,
,
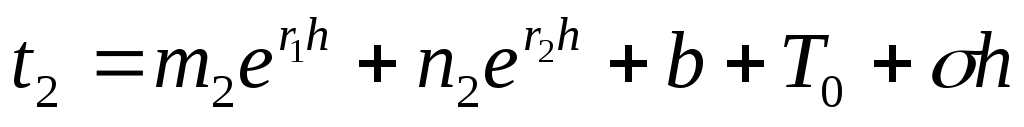 , (17)
, (17)
где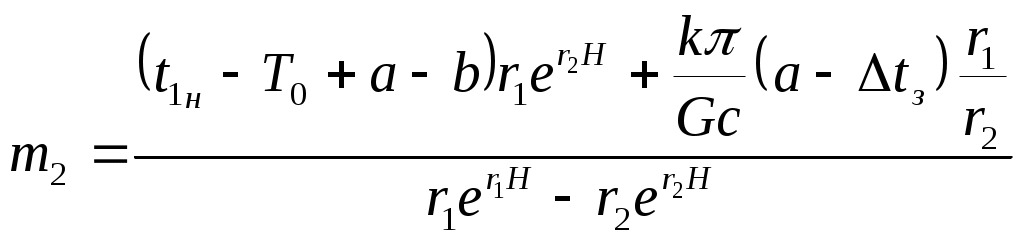 ;
;
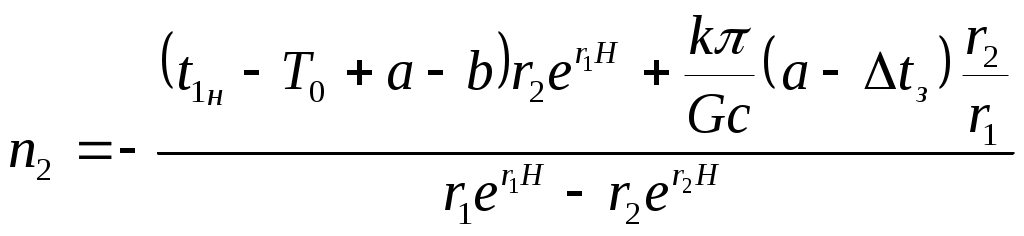 .
.
Аналитические выражения (16) и (17) являются математической моделью температурного режима бурящейся скважины. Они позволяют определить температуру в любой точке в любой момент времени от начала циркуляции и применимы при промывке глинистыми растворами, водой, продувке воздухом, причем как в случае бурения в мерзлых породах, так и в обычных условиях.
Для правильного решения задачи теплообмена необходимо определить входящие в математическую модель величины и коэффициенты.
Коэффициент kτ в критериальной (безразмерной) форме выражается зависимостью
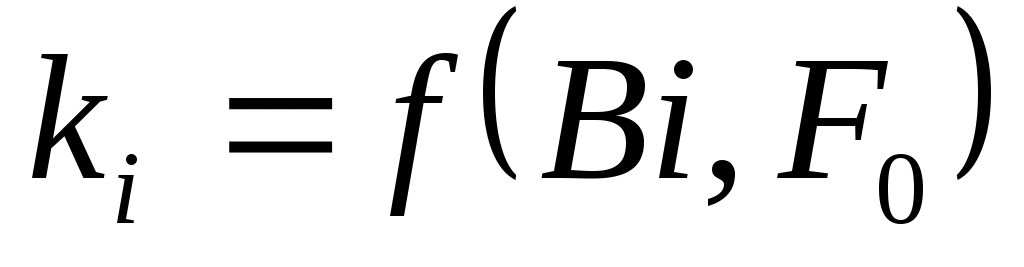 ,
,
где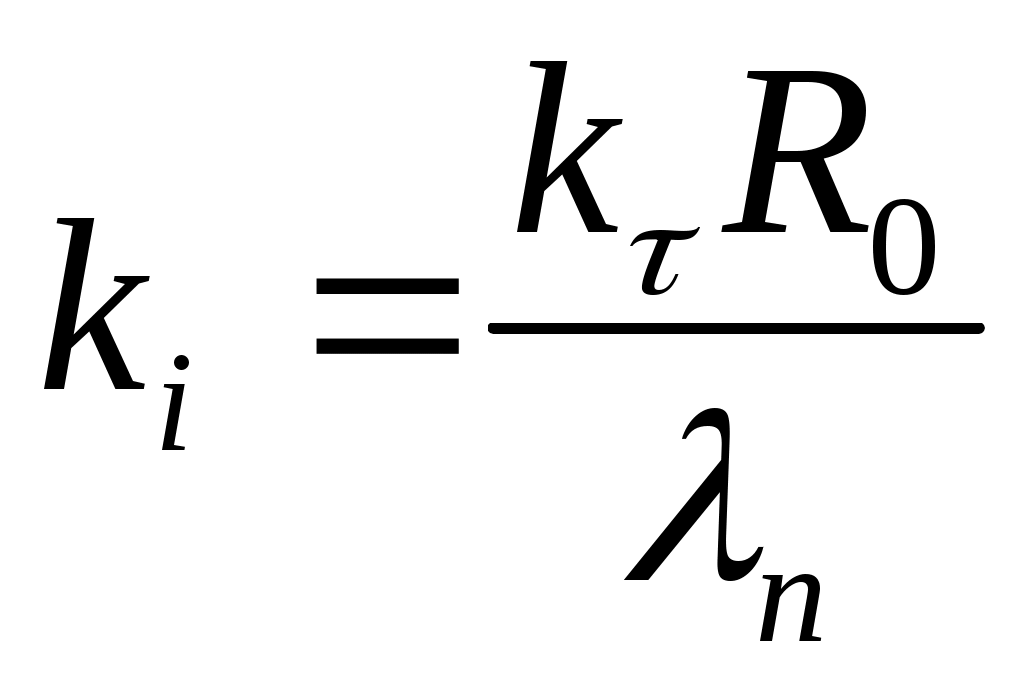 – безразмерный коэффициент нестационарного теплообмена (критерий Кирпичева); Bi – критерий граничных условий Био
– безразмерный коэффициент нестационарного теплообмена (критерий Кирпичева); Bi – критерий граничных условий Био 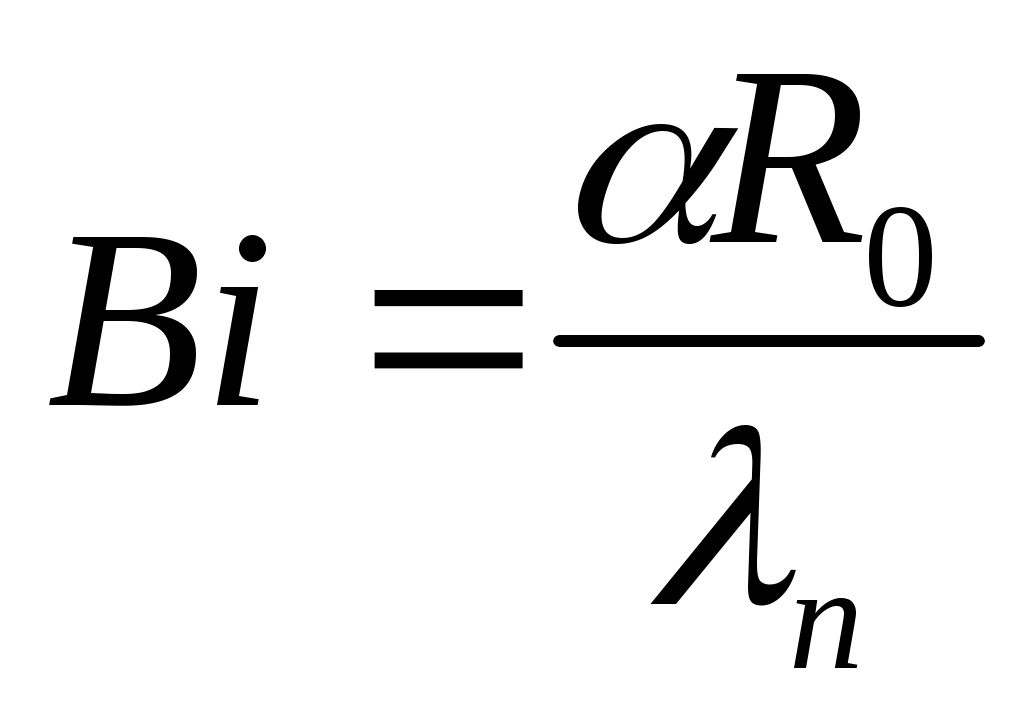 ;
; 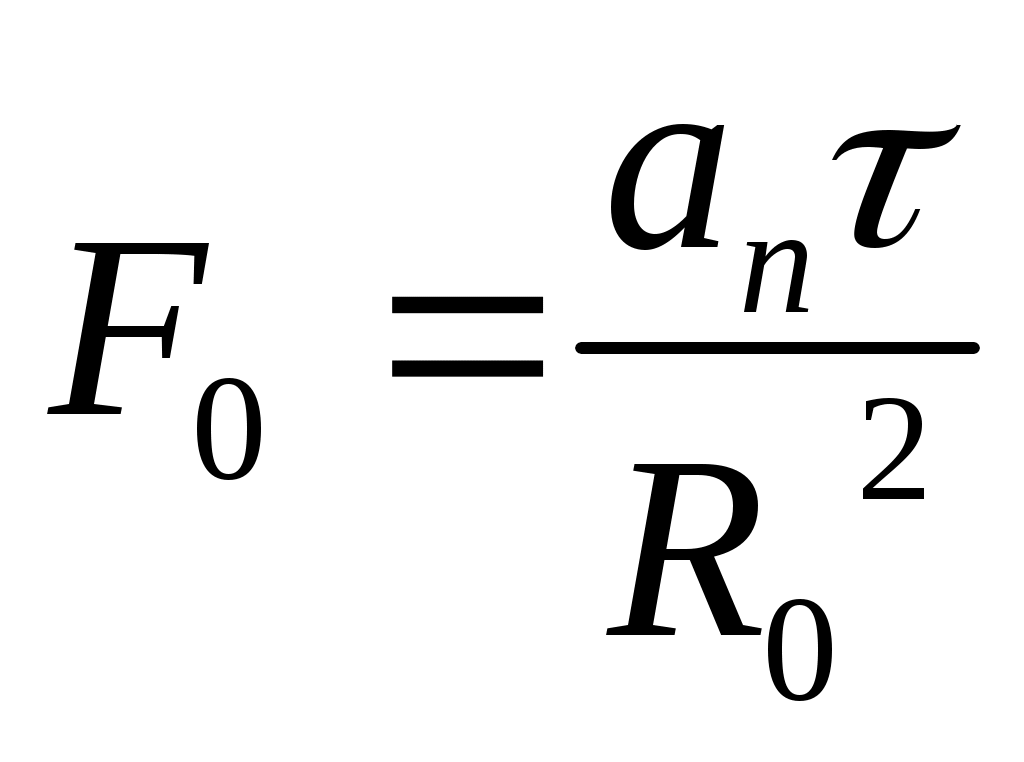
Циркул. систему разбивают на участки с одинаковыми геометрическими характеристиками канала: 1). кольцевой зазор между БК и обсадной колонной; 2). кольцевой зазор между БК и стенками скважины; 3). кольцевой зазор между УБТ и стенками скважины; 4). внутренний канал УБТ; 5). внутренний канал БК.
На забое
ТЕМПЕРАТУРНЫЙ РЕЖИМ СКВАЖИН
Важность:
-
многолетнемерзлые породы, сцементированные льдом -
глубокие скважины (высокие забойные температуры) -
высокие геометрические градиенты (месторождения парогидротерм)
Температурный режим – распределение температуры циркулирующего очистного агента во внутреннем канале БК и в кольцевом канале скважины.
Нисходящий поток (в буровых трубах) находится в состоянии теплообмена с восходящим потоком в кольцевом канале, который изменяет свою температуру также и за счет теплообмена с породами.
Процесс теплообмена нестационарный, зависит от продолжительности циркуляции.
В призабойной зоне очистной агент нагревается за счет теплоты, генерируемой породоразрушающим инструментом.
Энергия, затрачиваемая на преодоление гидравлических (или аэродинамических) сопротивлений, рассеивается в виде теплоты (диссипация энергии), что также оказывает влияние на температурный режим. Самостоятельным источником теплоты является трение буровых труб о стенки скважины.
При бурении с продувкой происходят также процессы массообмена (изменение влажности воздуха или газа), что существенно влияет на температуру.
При бурении в многолетнемерзлых породах теплообменные процессы осложняются изменениями фазового состояния влаги в породах, что сильно влияет на направление и интенсивность тепловых потоков.
Основные факторы, влияющие на температурный режим:
1). расход и начальная температура очистного агента;
2). скорость течения и турбулентность потоков;
3). физические и теплофизические свойства очистного агента и горных пород;
4). естественная температура пород и характер ее изменения по глубине;
5). конструкция БК и свойства материала;
6). скорость бурения и продолжительность рейса;
7). мощность, генерируемая породоразрушающим инструментом;
8). фазовые превращения влаги в горных породах и др.
Решение, полученное Б.Б. Кудряшовым в 1964 г.
Рассмотрим бурение скважины в мерзлых породах при прямой циркуляции очистного агента.

Очистной агент нагнетается в БК с начальной температурой t1н. При движении вниз он охлаждается в результате теплообмена через стенку буровых труб с более холодным очистным агентом. В зоне забоя очистной агент нагревается на Δtз за счет теплоты, генерируемой породоразрушающим инструментом.
При течении вверх по кольцевому каналу очистной агент охлаждается за счет теплообмена с мерзлым массивом. Начиная с некоторой глубины, начинается нагрев в результате интенсификации теплообмена с теплым нисходящим потоком.
Для составления дифференциальных уравнений теплообмена примем допущения:
1). естественная температура пород возрастает с глубиной прямолинейно;
2). физические и теплофизические свойства очистного агента постоянны, а их величины принимаются при средних значениях t и p.
3). физические и теплофизические свойства горных пород по глубине скважины постоянны;
4). коэффициент нестационарного теплообмена kτ между очистным агентом и массивом пород зависит от продолжительности циркуляции (рейса бурения) и не зависит от изменяющейся во времени температуры очистного агента;
5). влияние фазовых переходов влаги, содержащейся в породах, на температурный режим скважины, вызывает интенсификацию теплообмена, которая может быть учтена с помощью коэффициента интенсификации теплообмена kагр;
6). при бурении с продувкой влияние массообмена (изменения влагосодержания воздуха) на температурный режим учитывается только в призабойной зоне.
Допущения 1, 2 и 3 общеприняты для аналитического решения задачи.
4: точное аналитическое решение для коэффициента kτ получено при условии постоянства температуры очистного агента. В действительности температура изменяется с течением времени. Погрешность может быть устранена применением среднеинтегрального по времени значения kτ".
В процессе непрерывного теплообмена kτмонотонно снижается и его среднее значение всегда больше конечного. Из-за прерывности процесса бурения при его возобновлении даже после длительного простоя мы имеем дело с массивом пород, затронутых тепловым влиянием очистного агента, т.е.
tст≠tп.ест..
Поэтому значение kτ″ должно быть ниже среднего за период непрерывной циркуляции (рейс).
Пренебрежение изменением температуры очистного агента в течение рейса и недоучет теплового влияния предыдущих рейсов в некоторой мере компенсируют друг друга.
5 – практически единственная возможность решения задачи в условиях изменения фазового состояния влаги в породах.
6 – для бурения с продувкой в мерзлоте воздух целесообразно охлаждать до отрицательных температур и осушать, поэтому его влажность при теплообмене с мерзлыми породами может только возрастать. Возможный прирост температуры при этом несколько снижается.
Выделим элементарный участок dh в части скважины, где очистной агент в направлении своего течения только охлаждается. Тогда нисходящий поток в единицу времени с учетом выделения теплоты за счет работы сил трения потока теряет количество теплоты
Количество теплоты, потерянной восходящим потоком
При этом температура в нисходящем потоке с глубиной уменьшится, в восходящем – возрастет =>
Подставим эти выражения в (1) и (2):
t– температура очистного агента,0C; T0– температура пород у поверхности,0C; h– глубина (текущая координата), м;G– массовый расход очистного агента, кг/с; c– удельная теплоемкость очистного агента, Дж/(кг·0C); D– диаметр скважины, м;k– коэффициент теплопередачи через стенку бурильной трубы, отнесенный к 1м трубы;g=9,81 м/с2;kагр– безразмерный коэффициент интенсификации теплообмена при изменении агрегатного состояния пород;kτ– коэффициент нестационарного (зависящего от времени) теплообмена между очистным агентом и горной породой, Вт/(м2·0C);i– гидравлический уклон (безразмерная величина);σ– геотермический градиент, 0C/м.
Индекс “1” – внутренний канал БТ,
“2” – кольцевой канал скважины. Индексы “н” и “к” – начальное и конечное состояние в соответствующем канале.
Поделим (3) и (4) на Gc и dh:
С помощью уравнения (5) выразим t2 и
Для установления связи только между t1 и h подставим выражения (7) и (8) в (5) и (6) и, после преобразований, получим
Получили неоднородное (с правой частью) линейное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Общее решение уравнения (9) имеет вид:
где c1 и c2 – постоянные интегрирования; r1 и r2 – корни характеристического уравнения
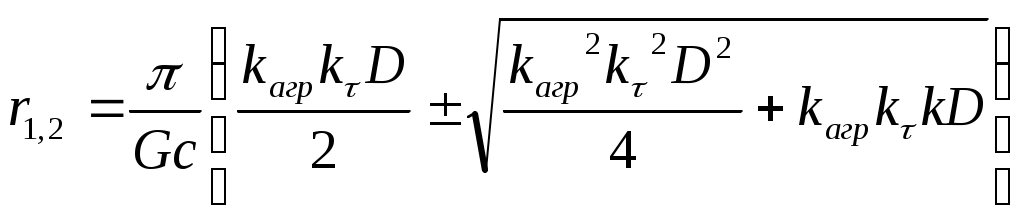 (11)
(11)Постоянные интегрирования определяются из граничных условий:
1. при h=0 t1=t1н, например, t1=150C.
2. в реальных условиях очистной агент на забое воспринимает теплоту, генерируемую породоразрушающим инструментом => на забое
Наряду с этим на забое и на любой глубине h должно соблюдаться условие (7), получим
Это второе граничное условие для нисходящего потока.
Итак, имеем 2 граничных условия:
при h=0 t1=t1н;
при h=H
На их основании из общего решения (10) получим
где H– глубина скважины, м.
Совместное решение (14) и (15) позволяет найти c1 и c2. Подставим их в общее решение (10). Температура в нисходящем потоке на любой глубине h
где
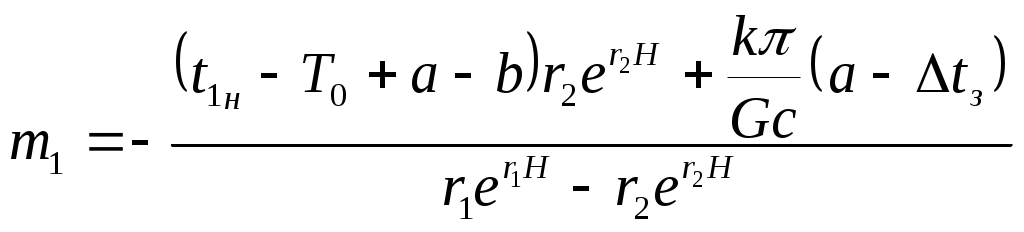 ;
;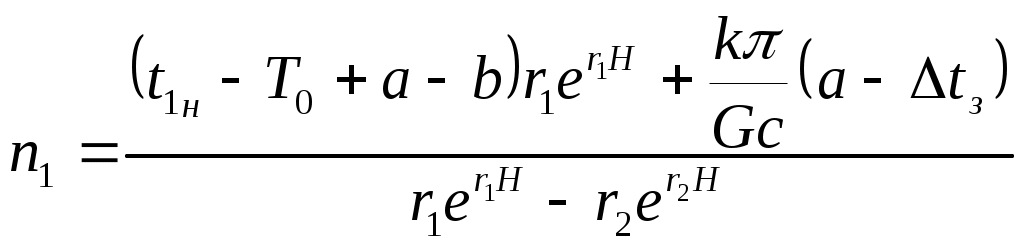 ;
;С помощью выражения (7) можно получить формулу для расчета t2.
С учетом того, что
где
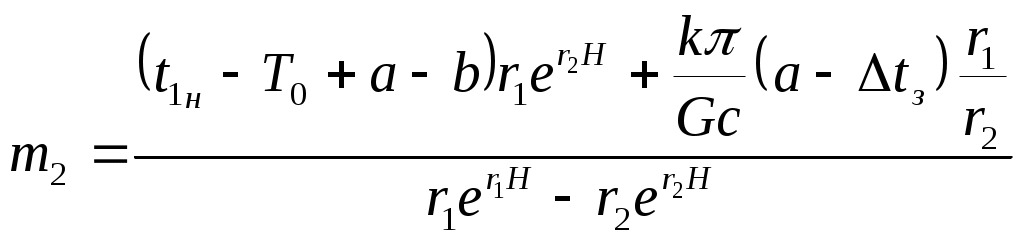 ;
;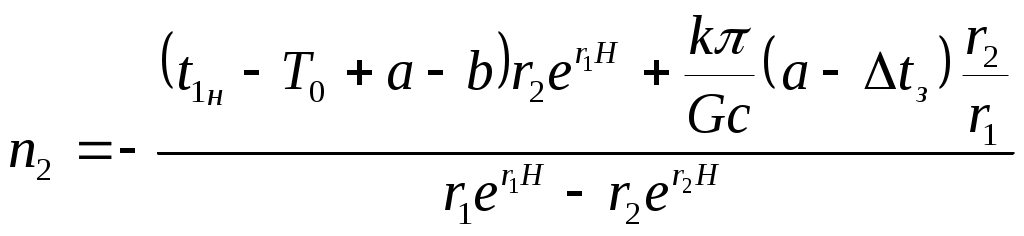 .
.Аналитические выражения (16) и (17) являются математической моделью температурного режима бурящейся скважины. Они позволяют определить температуру в любой точке в любой момент времени от начала циркуляции и применимы при промывке глинистыми растворами, водой, продувке воздухом, причем как в случае бурения в мерзлых породах, так и в обычных условиях.
Для правильного решения задачи теплообмена необходимо определить входящие в математическую модель величины и коэффициенты.
Коэффициент kτ в критериальной (безразмерной) форме выражается зависимостью
где