Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 174
Скачиваний: 3
СОДЕРЖАНИЕ
Глава 1. Понятия об основных алгебраических структурах.
§1. Алгебры. Подалгебры. Гомоморфизмы алгебр.
§3. Подгруппа. Достаточные условия подгруппы.
Глава 2. Матрицы и определители.
§1.Матрицы. Группа и кольцо матриц.
§2. Определители, их свойства.
Глава 3. Системы линейных уравнений, методы их решения.
Глава 5. Теория делимости в кольце Z.
§1. Отношение делимости в Z и его свойства.
§3. Взаимно простые числа и их свойства.
§4. НОК целых чисел и его свойства.
§5. Простые числа и их свойства.
Глава 6. Теория делимости в кольце Р[х].
§2. Отношение делимости в кольце Р[х] и его свойства.
Свойства отношения делимости в кольце Р[x].
§3. Деление с остатком в кольце P[x].
§4. Приводимые и неприводимые многочлены
Практическое занятие №1.
Алгебры, подалгебры, гомоморфизмы алгебр.
1. Выяснить, является ли алгеброй декартов квадрат R2=RхR относительно операции "сложения" его элементов (а, b) + (с, d) = (а + с, b + d).
2. Проверить, образует ли алгебру множество радиус-векторов, расположенных в первой четверти координатной плоскости, относительно операций:
а) сложения векторов плоскости;
б) вычитания векторов плоскости.
3. Является ли алгеброй множество N относительно следующих действий:
а) а*b = а2 - 2ab + b2;
б) a*b = a2-b2.
4. Является ли алгеброй множество Z относительно следующих действий:
а) а*b = [(а-b)3 - (а+b)3] / 3;
б) a*b=[(a-b)2 + (a+b)2]/2.
5
1, при n=1,
является гомоморфизмом данных алгебр. Определить вид гомоморфизма.
6. Является ли гомоморфизмом (и какого вида) отображение : хх2 алгебры
на себя ?
7. Является ли отображение : х2х гомоморфизмом (и какого вида) алгебрыв алгебру ?
8. Выяснить, какое из следующих соответствий является гомоморфизмом алгебры R, - > на себя и какого вида:
а) (х) = 2х, г) (х) = 0,
б) (х) = х/3 д) (х) = | х |.
в) (х) = х2, е) (х)=1.Практическое занятие №2.
Группа, аксиомы группы. Подгруппа.
Достаточные условия подгруппы.
1. Выяснить, какие из следующих алгебр являются группами:
a), где * : хх+1, ;
б), где + : (а,b,с) а+b+с,
b) <Z.-,+>,
г),
д),
e).
2. Доказать, что следующие алгебры являются аддитивными группами:
a) <2Z, +>, б), в)5, +>,
г), д) , e) 6, +>.
3. Доказать, что следующие алгебры являются мультипликативными группами:
a), 6) +, •>, в) <{2к}, •>.
4. Показать, что алгебра+, T> является полугруппой и найти нейтральный элемент (когда он имеется), если операция Т задана так:
а) аТb = а(1-b)+b, в) аТb = 2аb-а-b+1,
б) аТb = 2b(а+1)+2а-1, г) аТb = -2а-2b + 6 + ab.
5. Доказать, что+, T> является коммутативной полугруппой, если операция Т задана так:
а)Т: (a,b) alg(b), б) Т: (a,b) ab/(a+b).
6. Показать, что <А, Т>, где А = [0, 1], а операция Т задана по правилу аТb = (a+b)/(l+ab), является полугруппой.
7. Найти нейтральный элемент е полугруппыи множество всех элементов, обладающих симметричными, моноида , если:
а) аТb = а + b - ab,
б) аТb = - а - b + ab + 2,
в) аТb = 2а+2b-2ab-1,
г) аТb = -2а -2b + 6 + ab.
8. Доказать или опровергнуть, что для любого множества А0 алгебра (А), > является группой, если операция задана по правилу: XY = (X\Y) (Y\X), где (А) - множество всех подмножеств множества А.
9. Показать, что Z, Т>, является группой, если
а) аТb = а + b + 3
б) аТb = а + b - 2.
10. Показать, что <{а+b3 / a,bQ},+> является подгруппой группы.
11. Показать, что <{а+b2 / (а2-2b2 = 1, a,bQ°), • > является подгруппой группы. где Q° = Q\{0}.
12. Дано Zp = {0, 1, 2,..., р-1} множество равноостаточных классов целых чисел. Z°p = Zp\{0}. При каких условиях Zo7oP, a Zo8 < ZoP. Практическое занятие №3.
Кольцо, поле, линейное пространство.
1. Выяснить, какие из указанных алгебр являются кольцами, полями и линейными пространствами над полем действительных чисел R.
1.+, •>;
2.;
3.
4.6, + ,
5.5, +, >:
6.;
7. R над Q;
8. Q над R;
9.1, +, {wl | lÎR}>, где R1 - множество радиус-векторов плоскости.
10.1, +, {wl | lÎR}>, где R1 - множество векторов на координатной прямой.
11. Множество радиус-векторов на любой прямой, проходящей через начало координат, относительно операции сложения векторов и умножения вектора на скаляр.
Практическое занятие №4.
Операции над матрицами. Свойства операций. Группа, кольцо и линейное пространство матриц.
1. Выполнить указанные действия: (3А + В)•С, если
A =, B =
, C =
.
2. Наиболее рациональным способом вычислить произведение матриц:•
•
•
.
3. А =, B=
. Найдите А*В
4. A=, B=
. Найдите А*В
5. A=, B=
, С=
. Найдите А*С+В.
4. Доказать, что множество квадратных матриц второго порядка образует группу по сложению.
5. Доказать, что множество квадратных матриц третьего порядка образует некоммутативное кольцо.
6. Доказать, что множество квадратных матриц второго порядка образует линейное пространство.
Практическое занятие №5.
Обратимые матрицы.
Условия обратимости матрицы.
Алгоритм нахождения обратной матрицы.
Решение матричных уравнений.
1. Вычислить строчный ранг матрицы и выяснить, имеет ли она обратную матрицу.
а) А =, б) В=
, в) С =
, г) А=
, д) А=
.
2. Доказать, что строчный ранг матрицы А равен ее столбцовому рангу.
3. Найти матрицу A-1
а) А =, б) А=
,
в) А =, г) А =
, д) A =
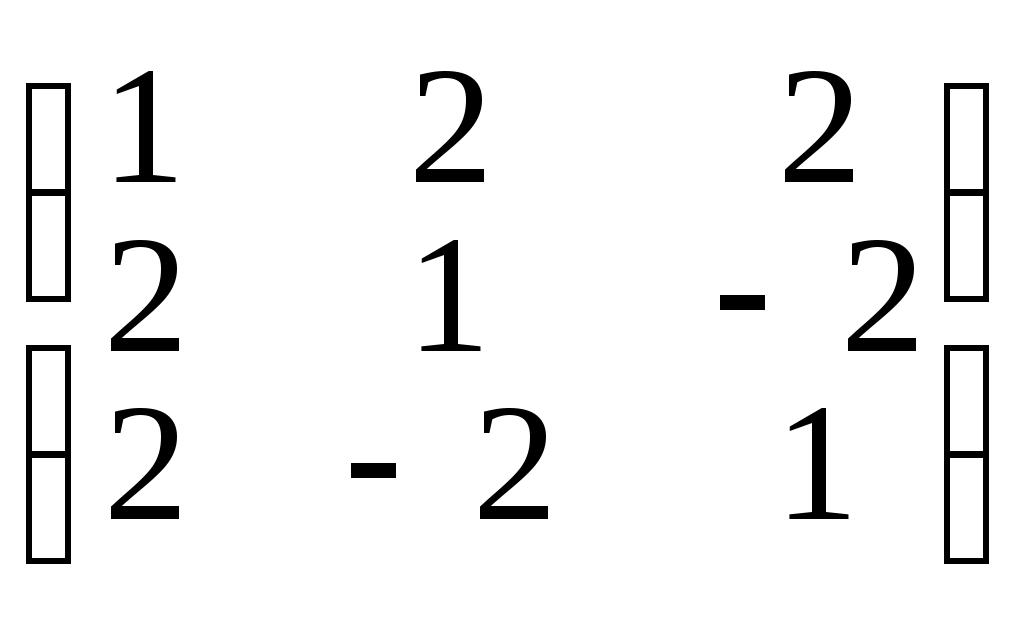
4. Имеет ли матрица А обратную матрицу A-1?
а) А =, б) А =
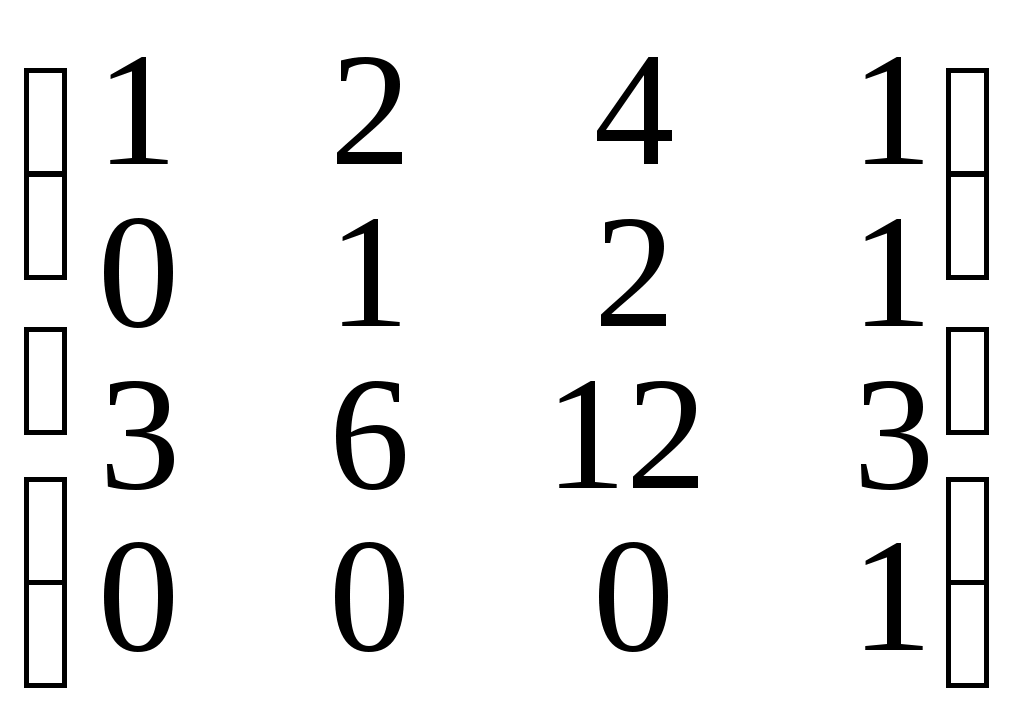
5. Решить матричные уравнения:
а) A•Х = В, если А-1 =, В =
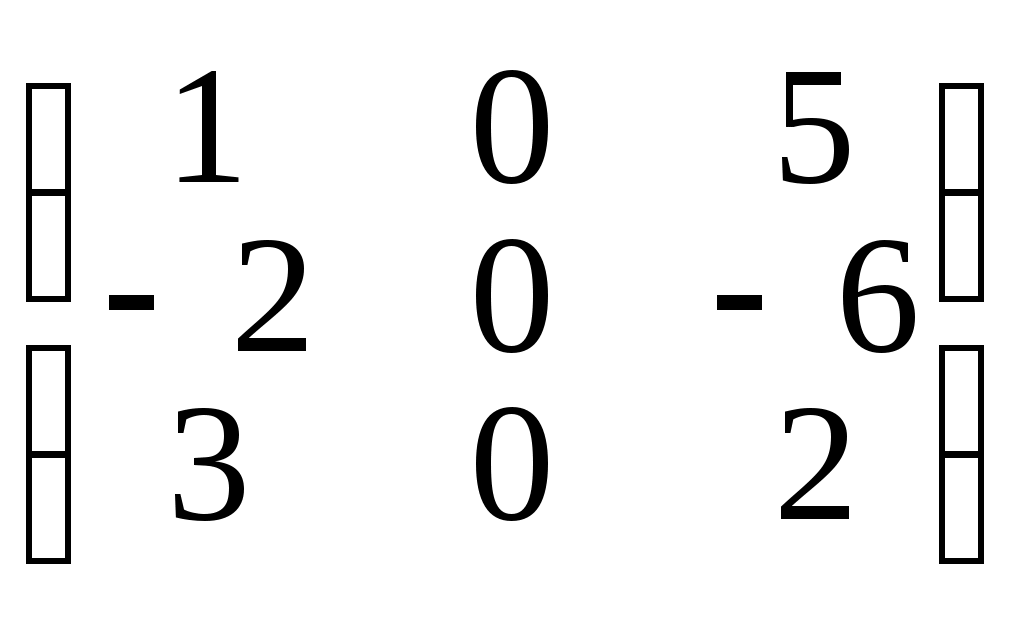
б) Х•А = В, если А =, В = (-1 -4 -2)
в) А•Х = В, если А=, В =
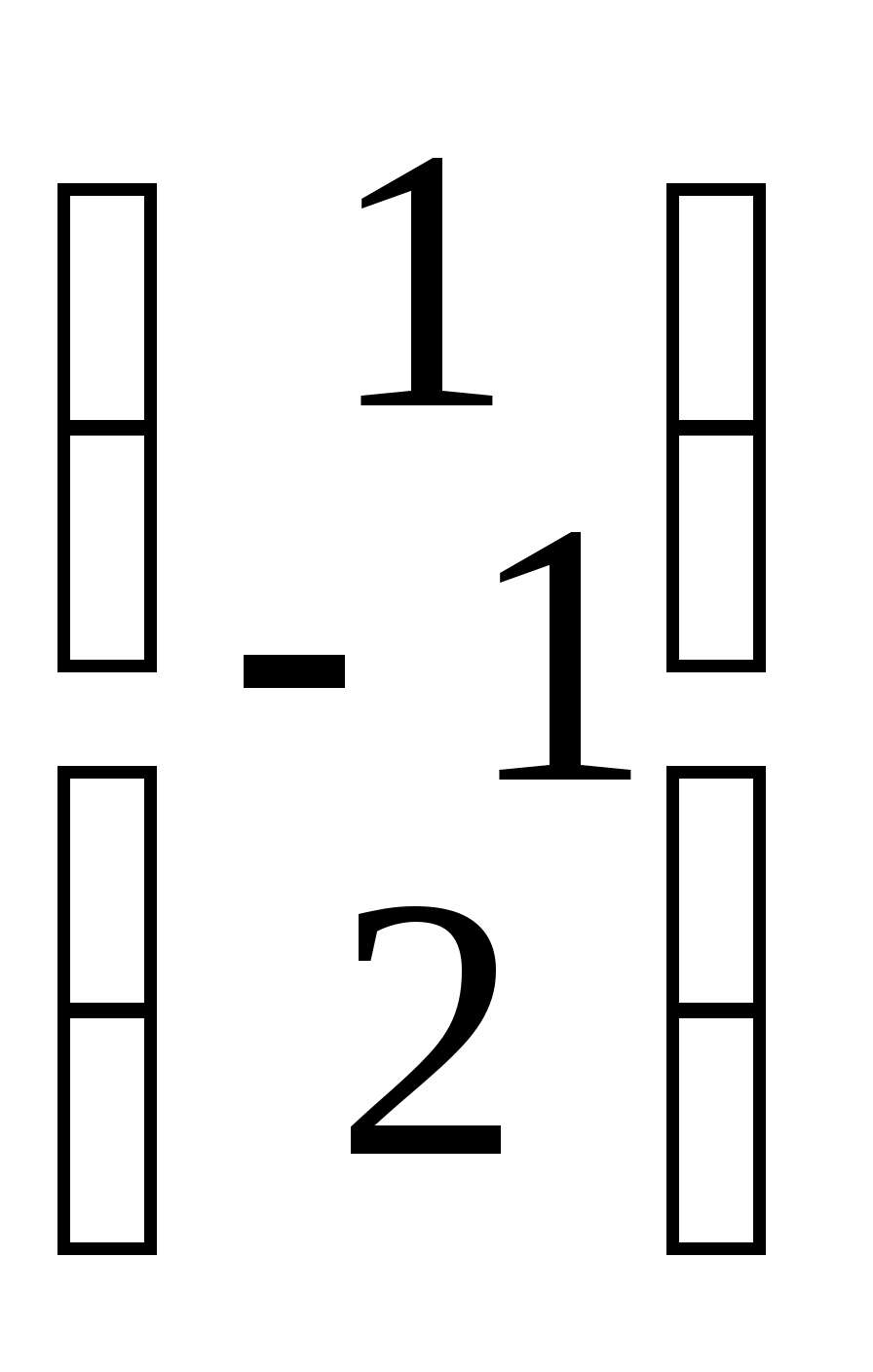
г)•X =
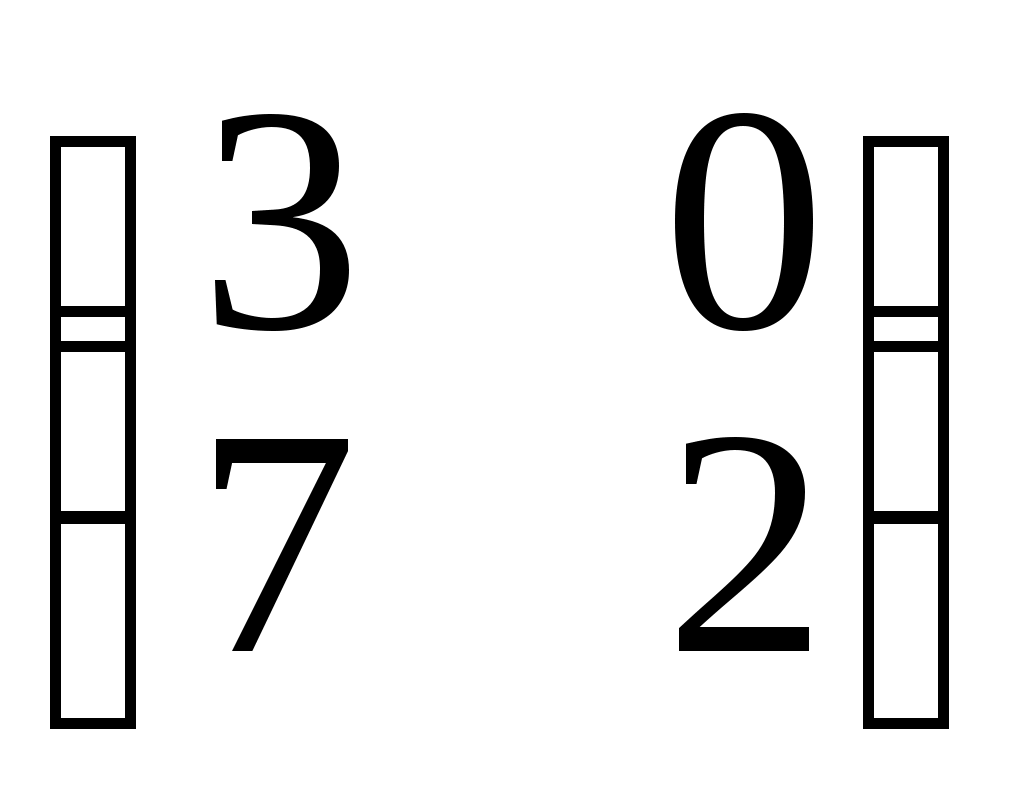
д)•X =
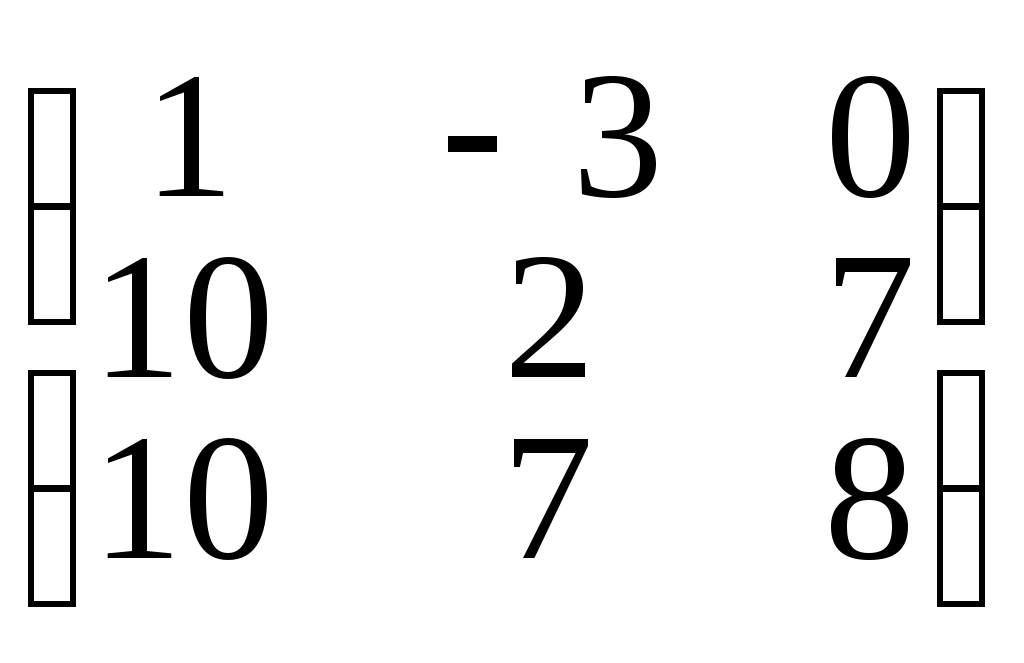
е)• X •
•
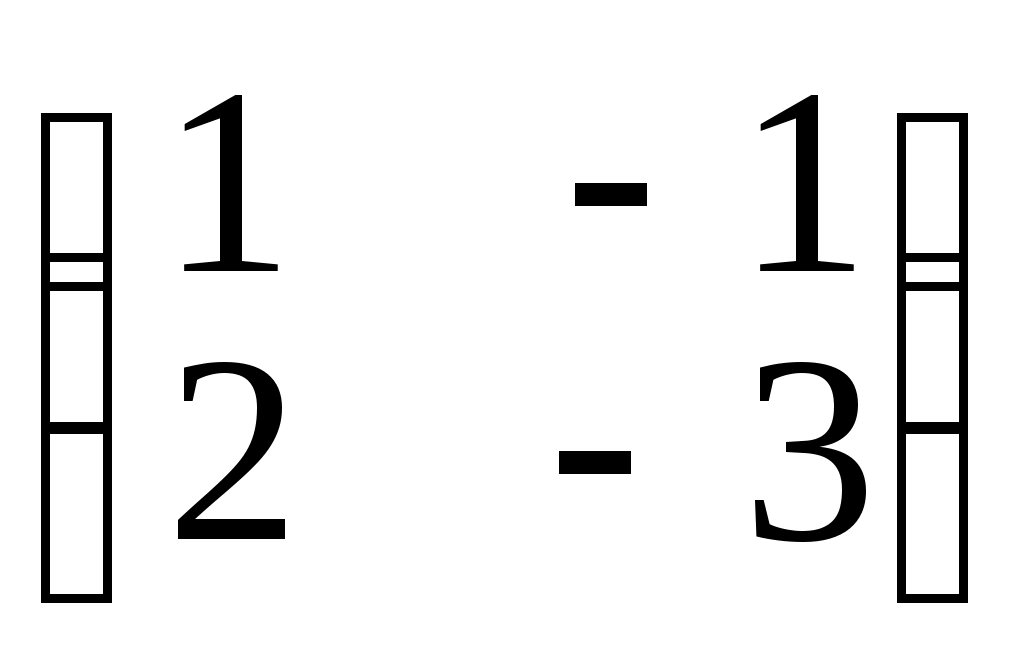
ж) X •=
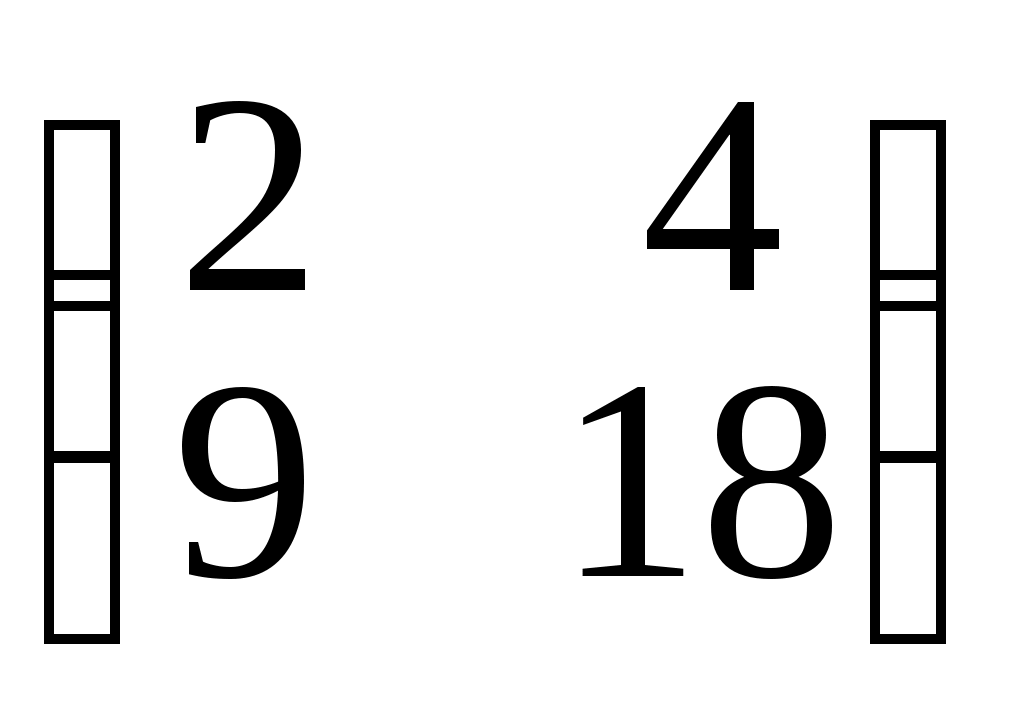
6. Вычислить степени матрицы.
а); б)
; в)
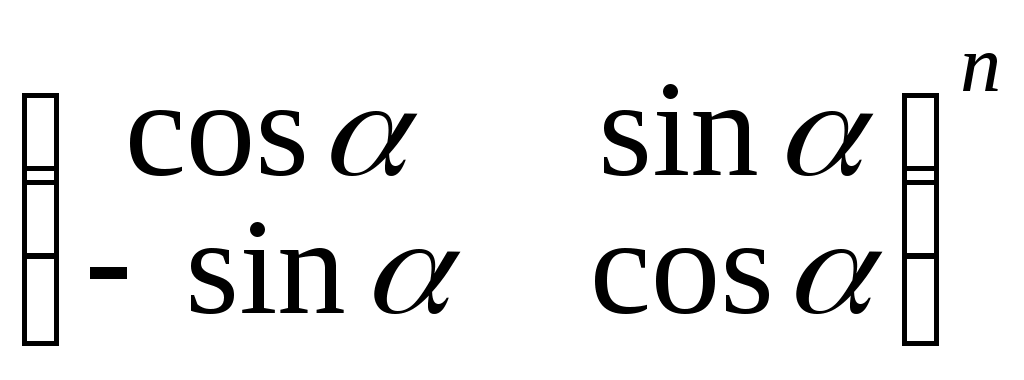 1 ... 8 9 10 11 12 13 14 15 16
1 ... 8 9 10 11 12 13 14 15 16
Практическое занятие №6
Перестановки и подстановки. Четные и нечетные подстановки. Определители второго и третьего порядков.
1. Определить четность и нечетность подстановок:
а) =
2. Найти А5 < n
3. Найти А4 < 4
4. Доказать, что τ =
5. Определить, с каким знаком входят в определитель 7-го порядка произведение
6. Выбрать значения i и k так, чтобы произведение
7. Вычислить определители:
а)
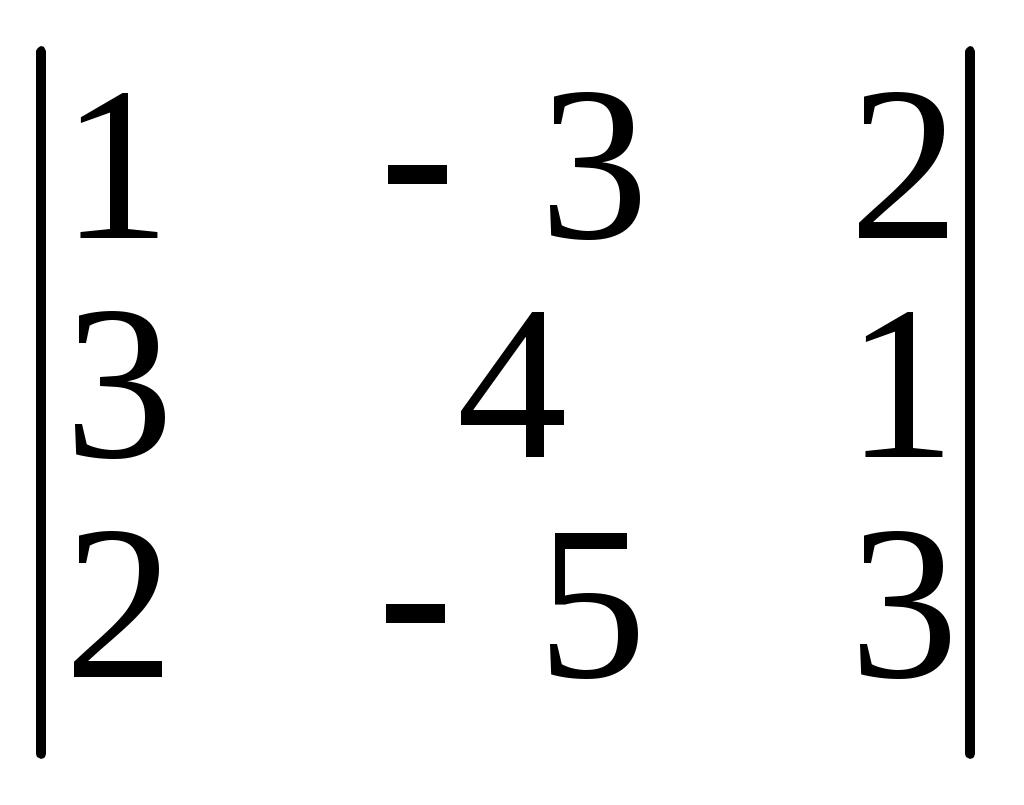 б)
б) 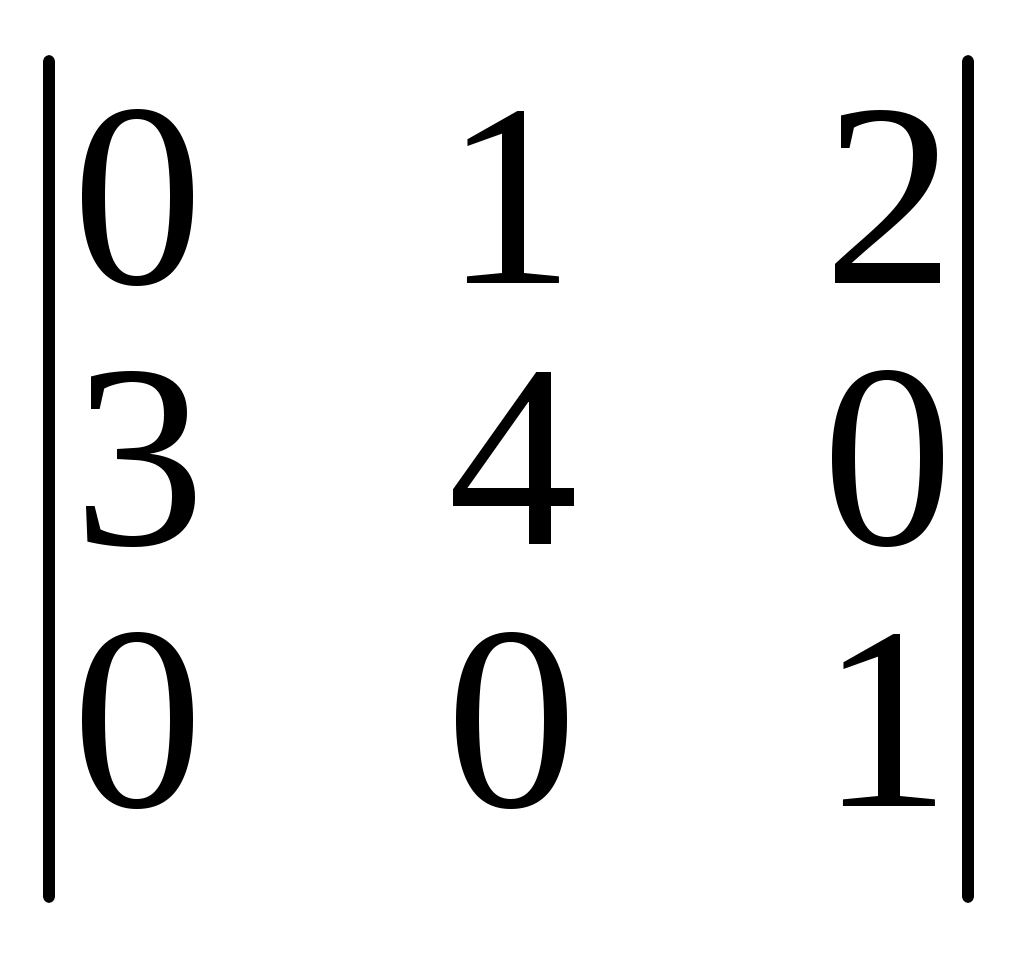 в)
в) 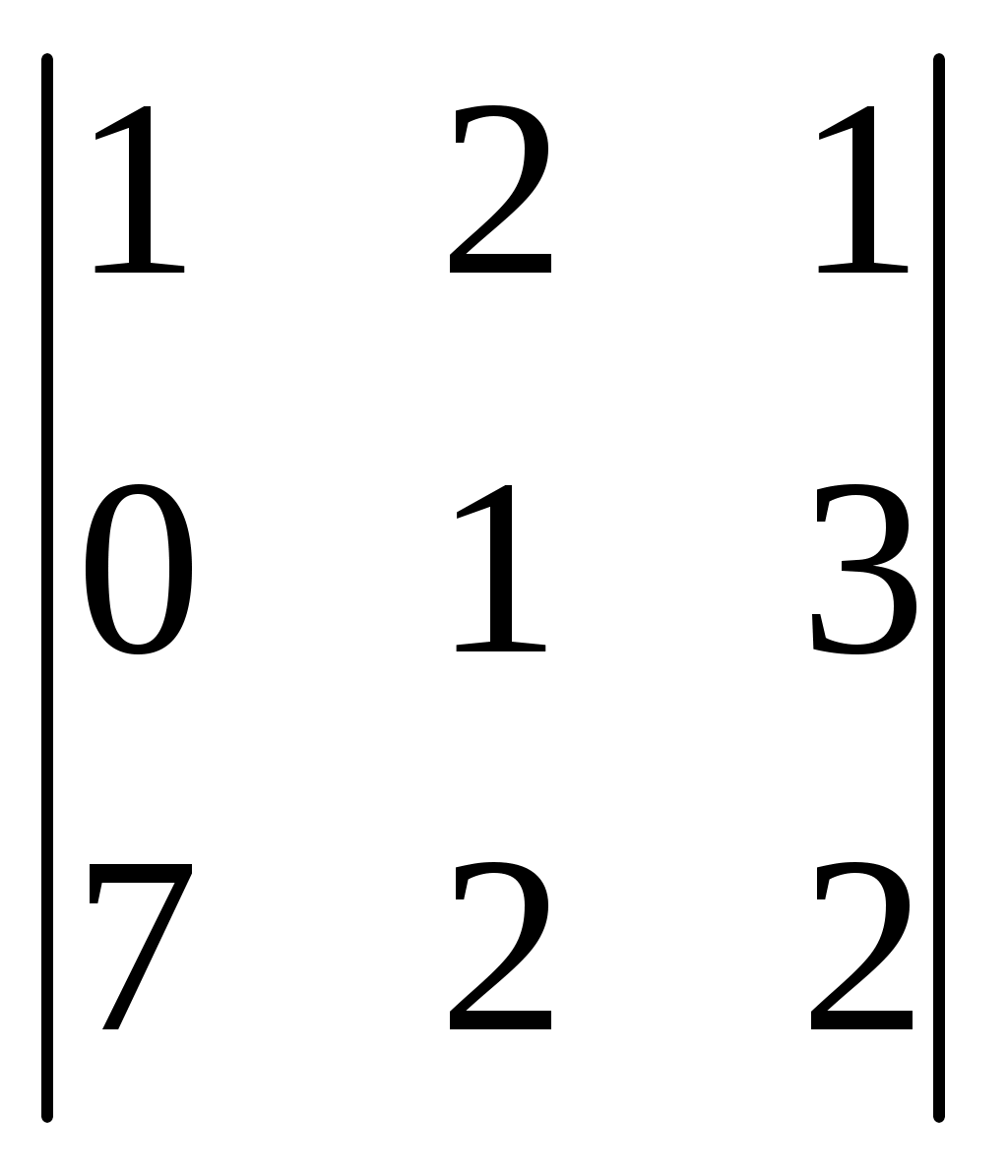
Практическое занятие №7
Определитель квадратной матрицы.
Миноры и алгебраические дополнения.
Способы вычисления определителя.
Вычислить определители:
1. а)
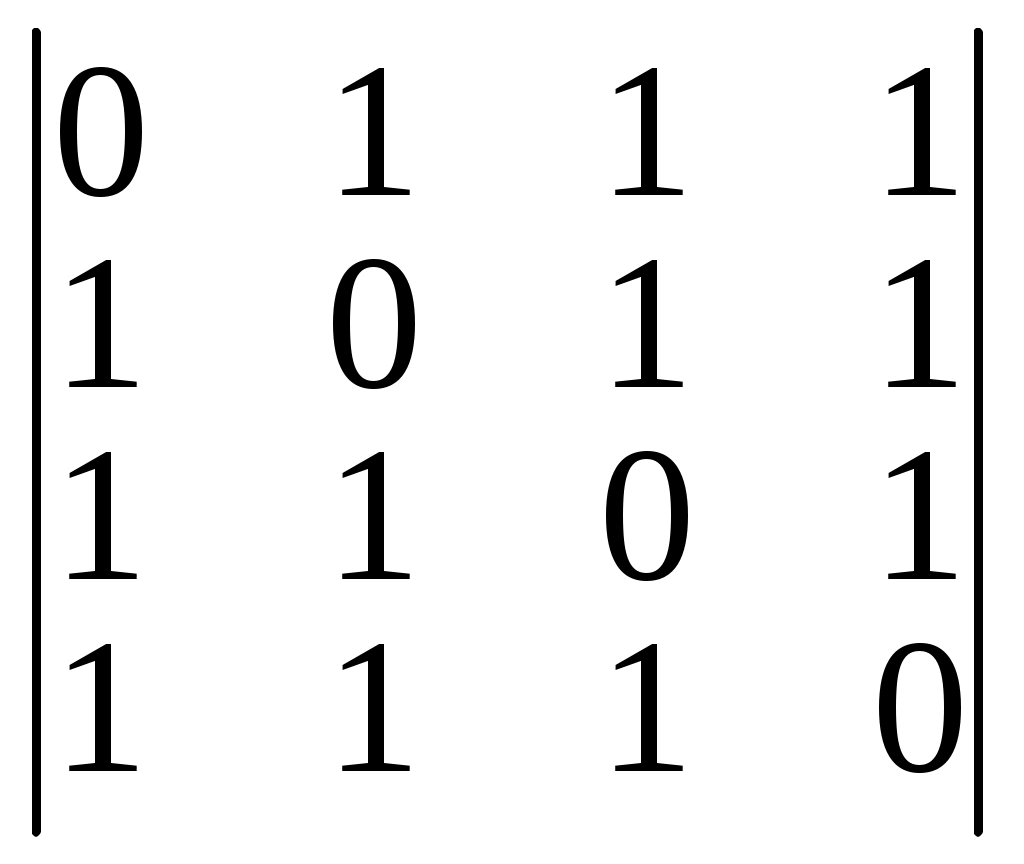 б)
б) 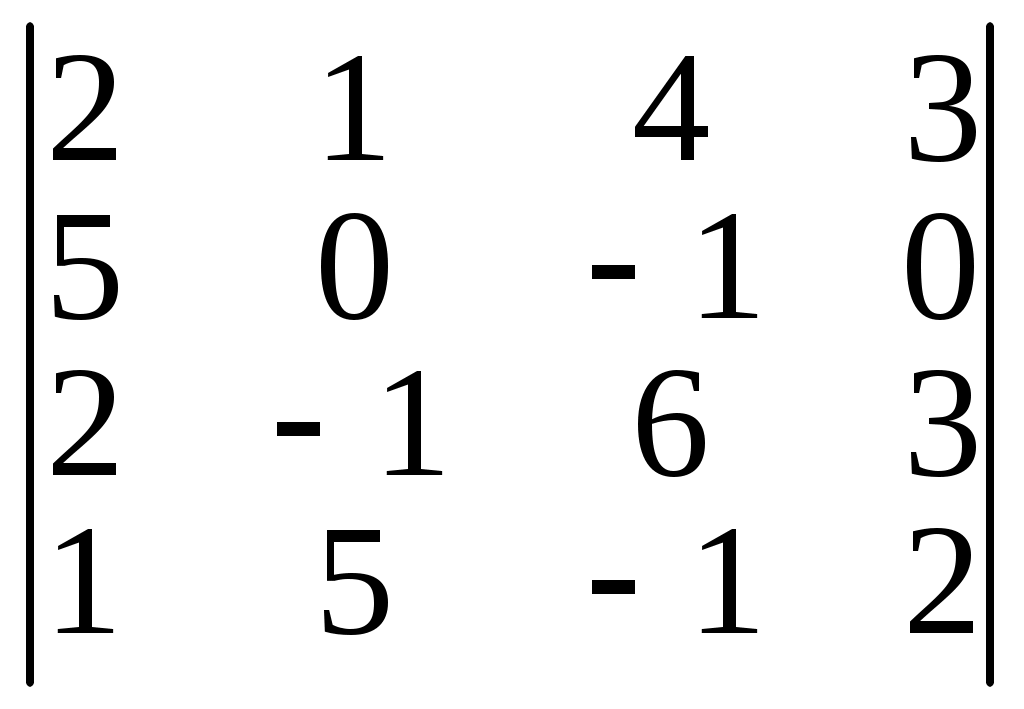 в)
в) 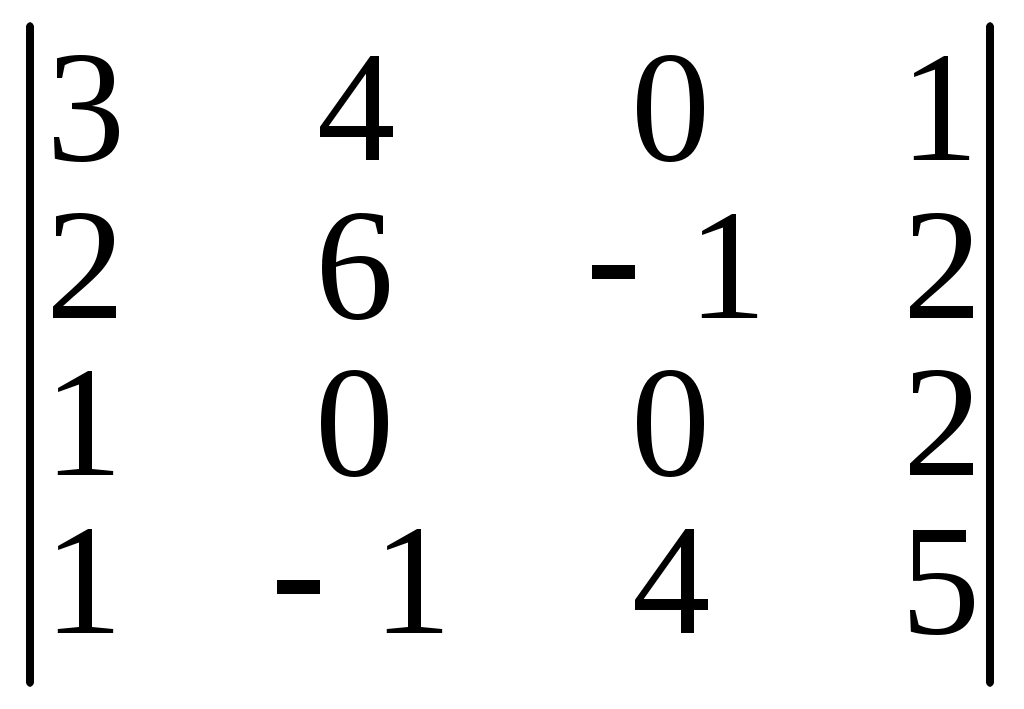
2. Вычислить:
а)
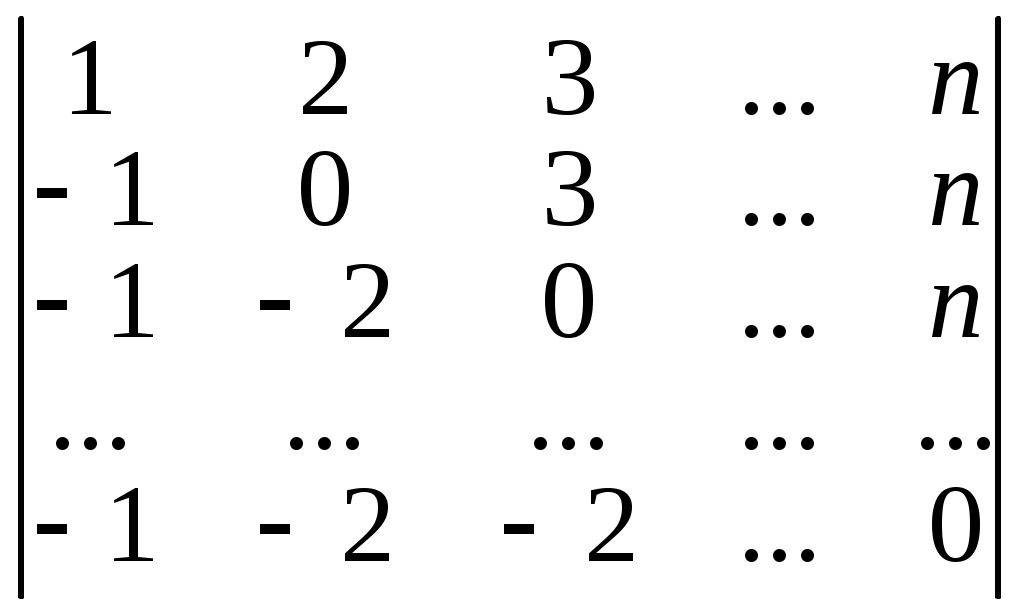 б)
б) 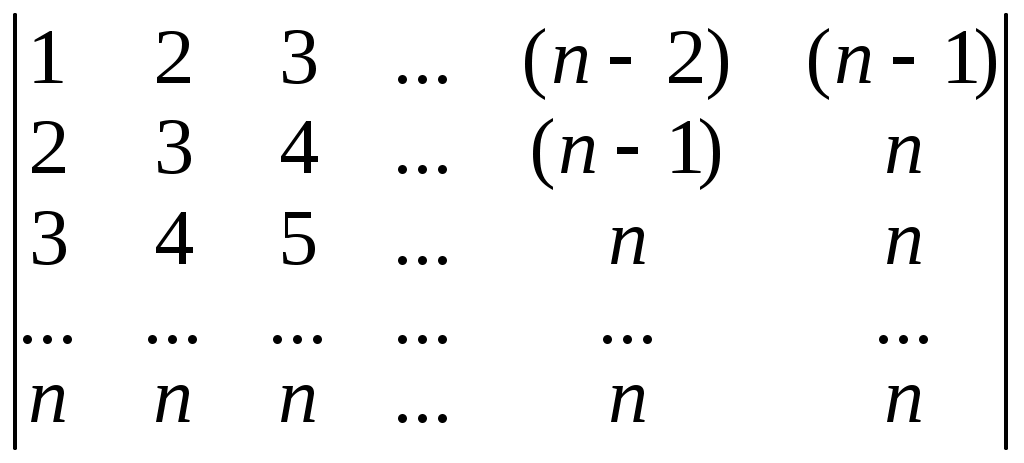
3. Найти миноры и алгебраические дополнения элементов определителя.
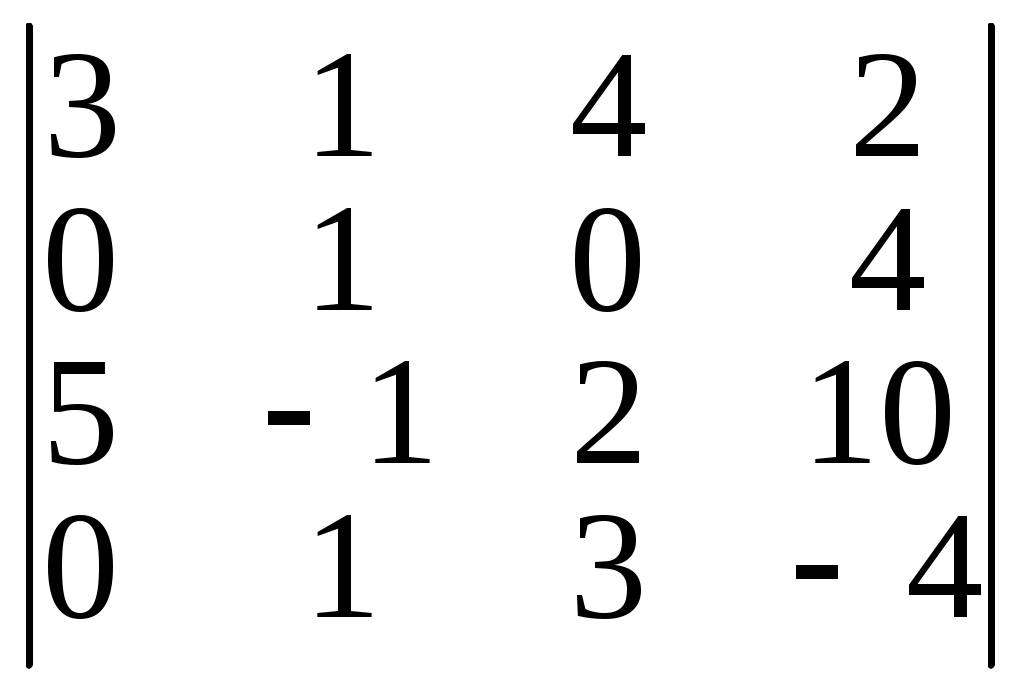 а) 13 б) 32 в) 41 г) 24
а) 13 б) 32 в) 41 г) 244. Разложить определитель по элементам первого столбца.
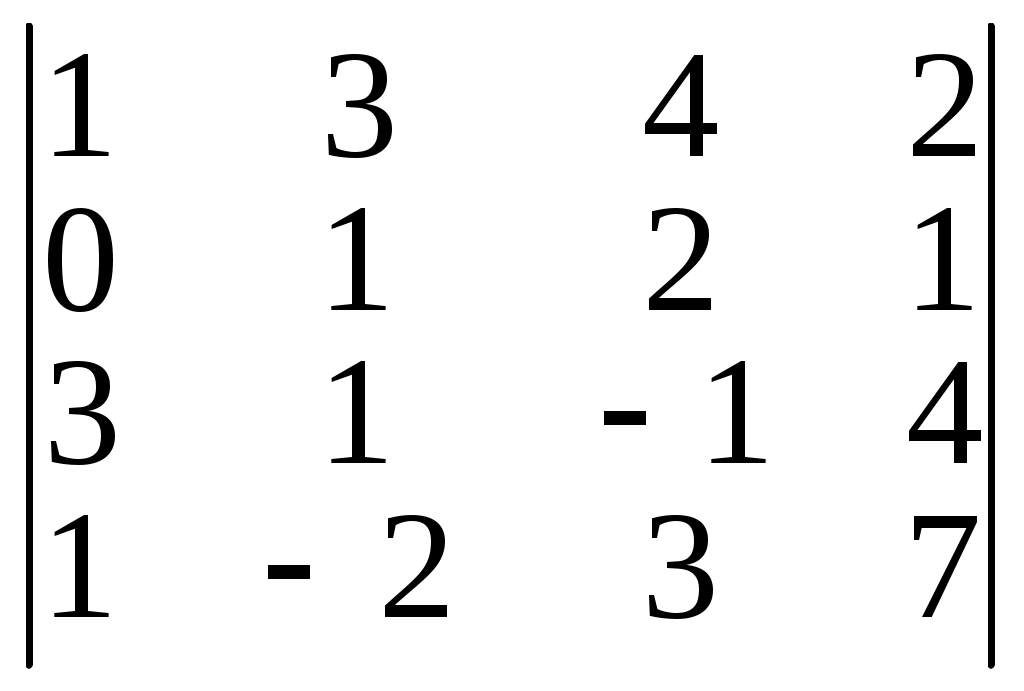
Практическое занятие №8
Системы линейных уравнений. Решение систем линейных уравнений методом Гаусса.
1. Решить системы линейных уравнений методом Гаусса:
а)
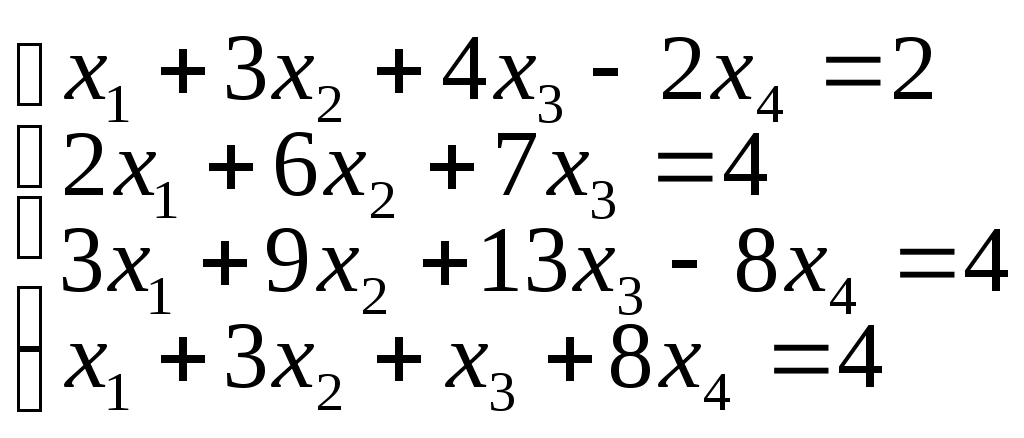 б)
б) 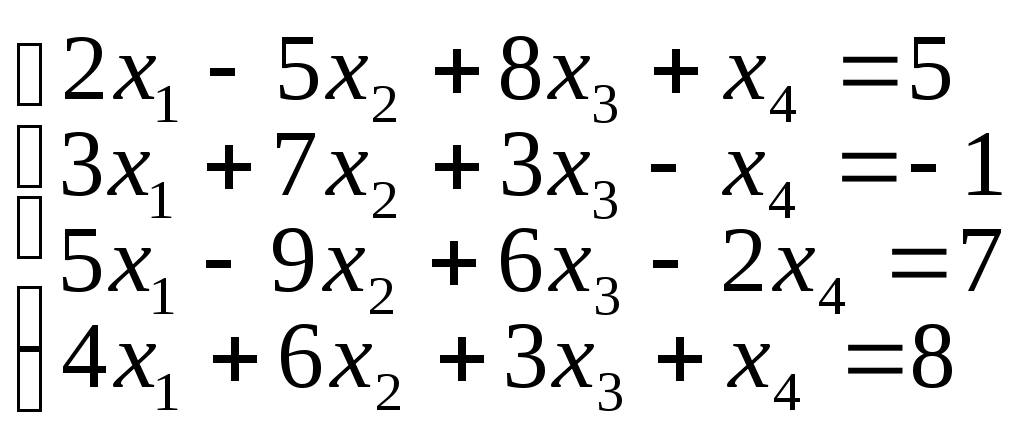
в)
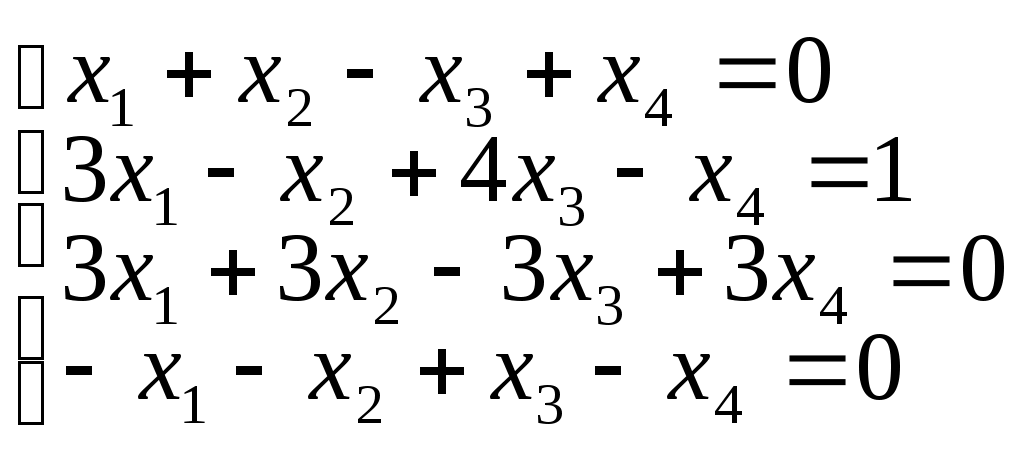 г)
г) 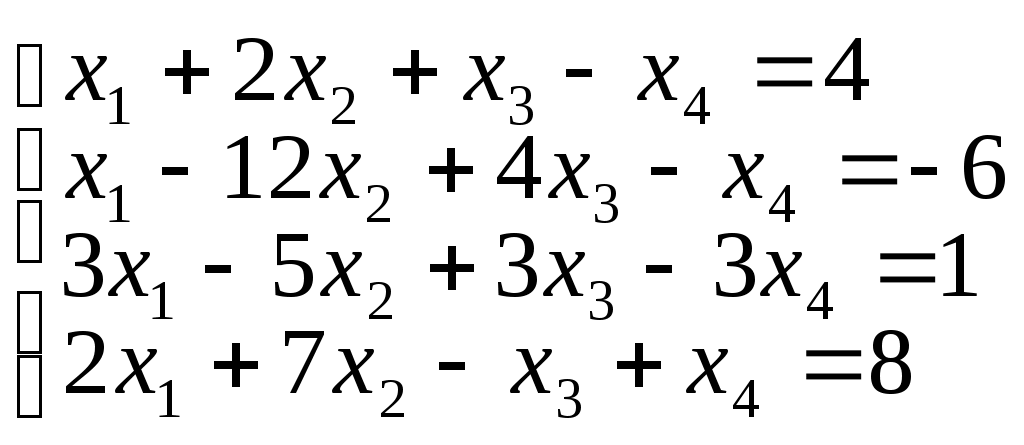
д)
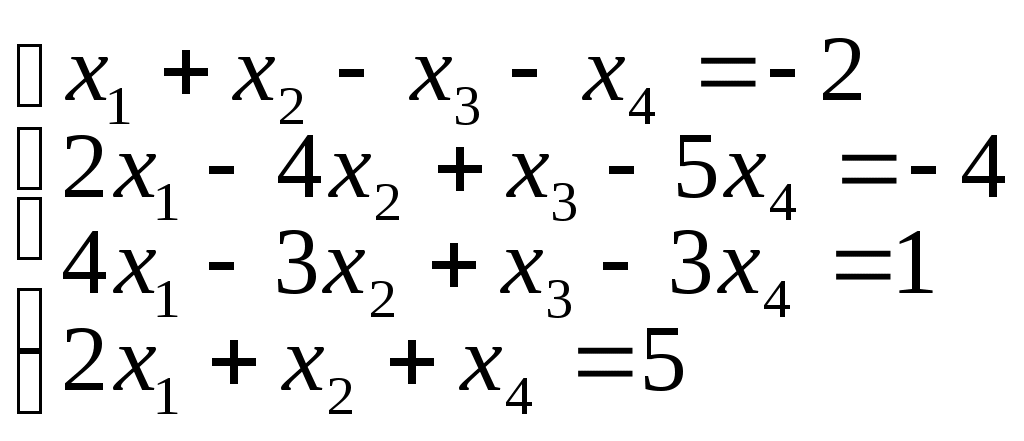 е)
е) 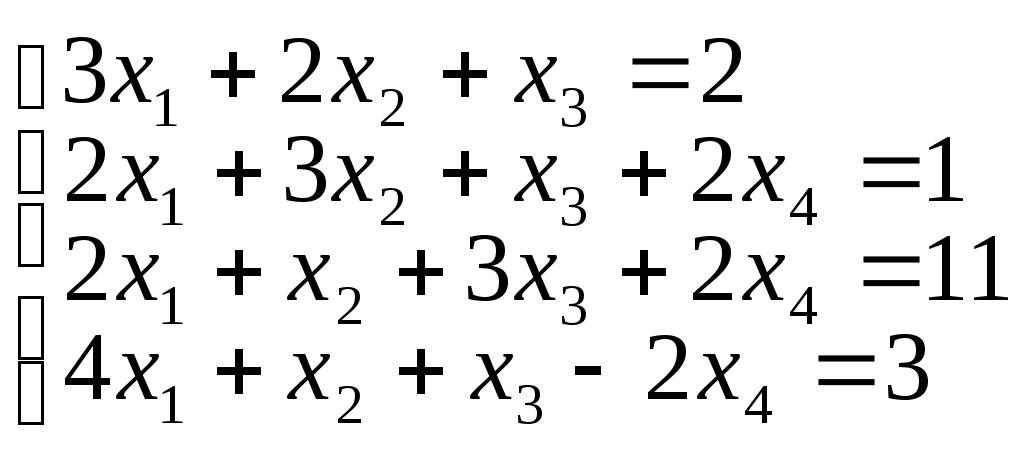
2. Докажите, что если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.
3. Докажите утверждение: если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
Практическое занятие №9
Решение систем линейных уравнений матричным методом
и по правилу Крамера.
1. Решить системы матричным методом.
а)
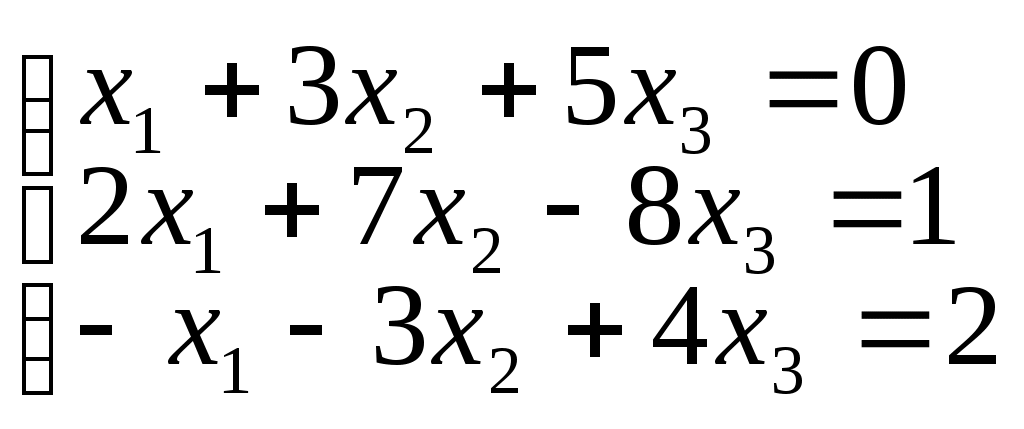 б)
б) 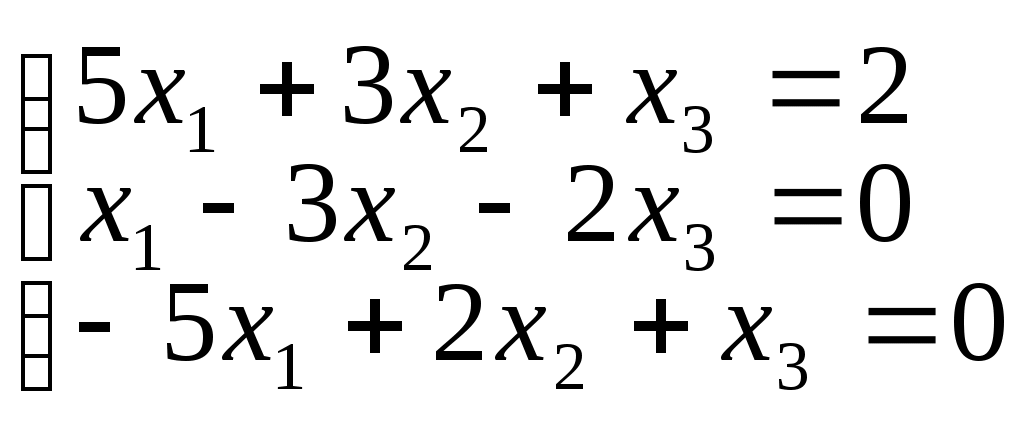
в)
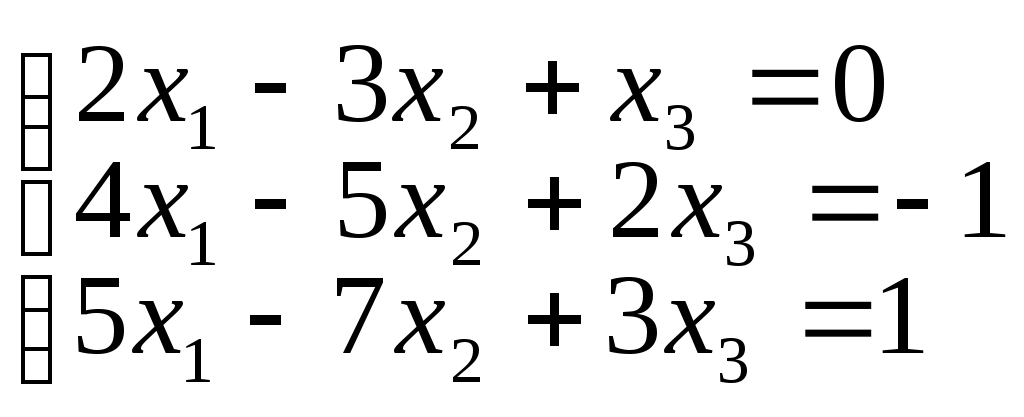 г)
г) 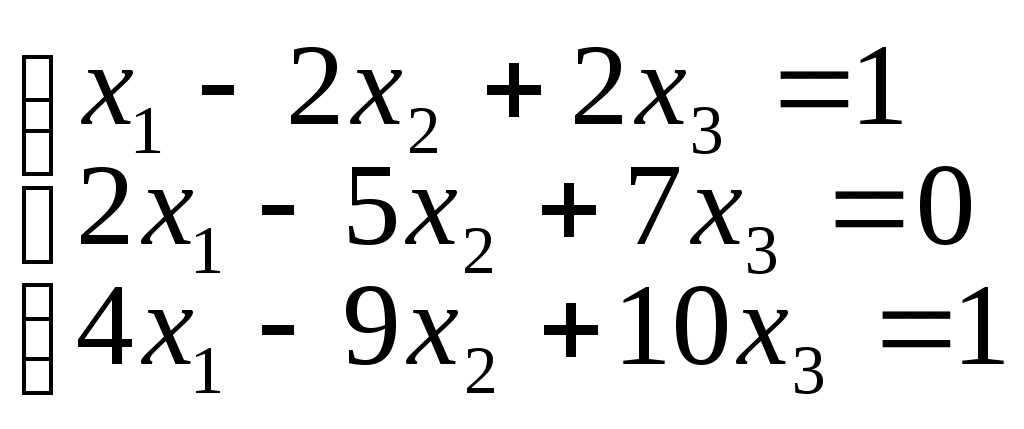
2. Решить системы методом Крамера:
а)
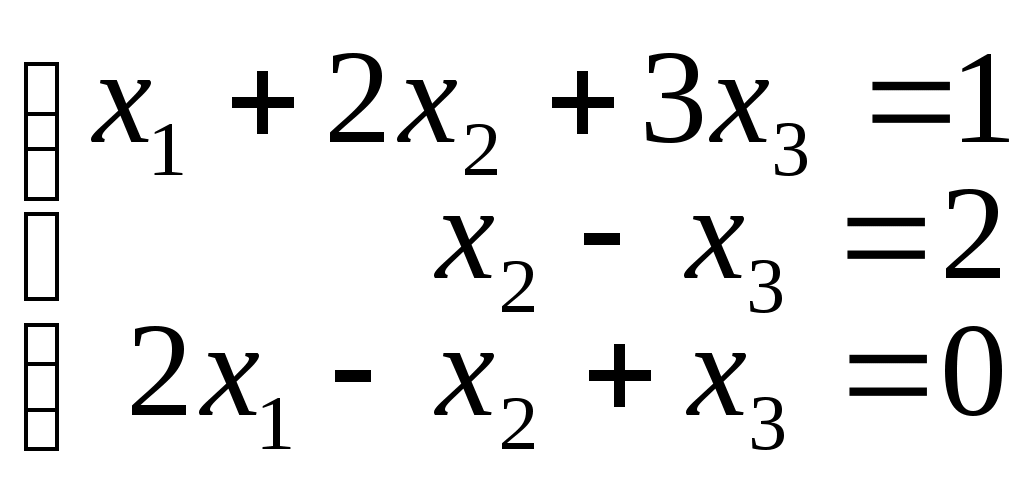 б)
б) 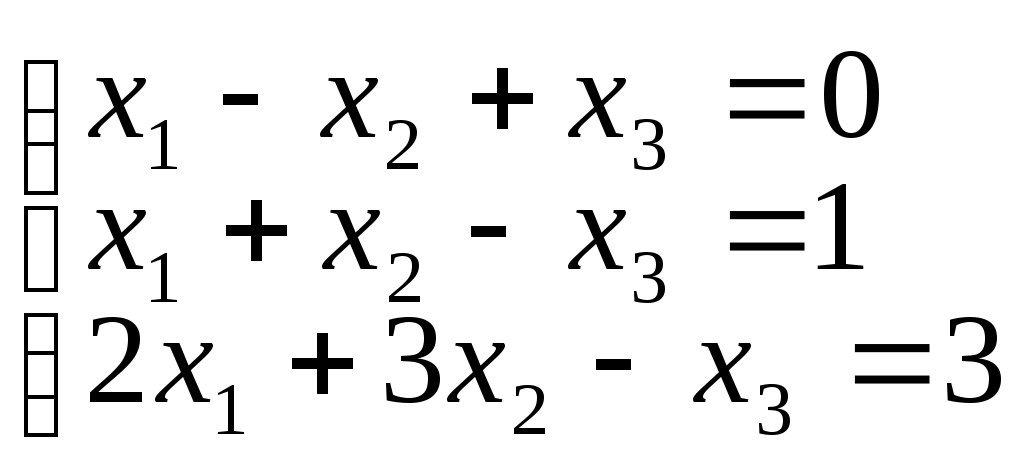
в)
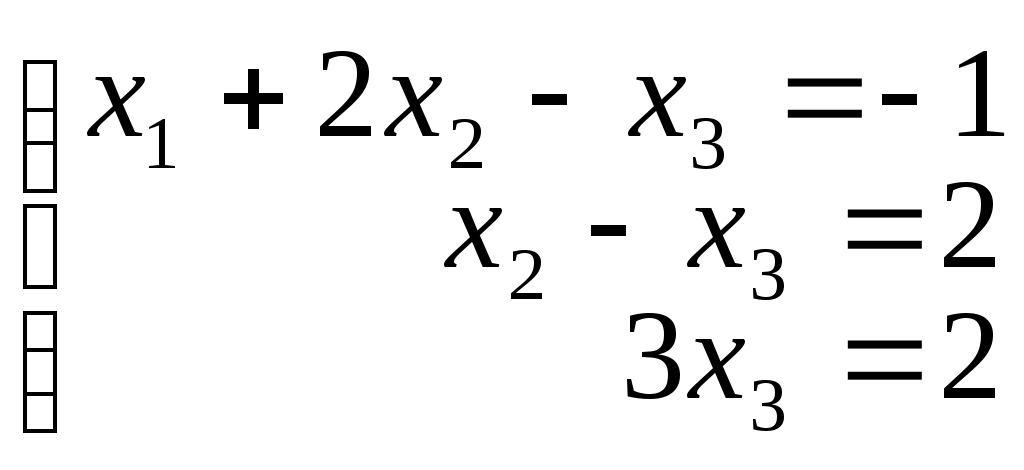
3. Найти Ф.С.Р.
а)
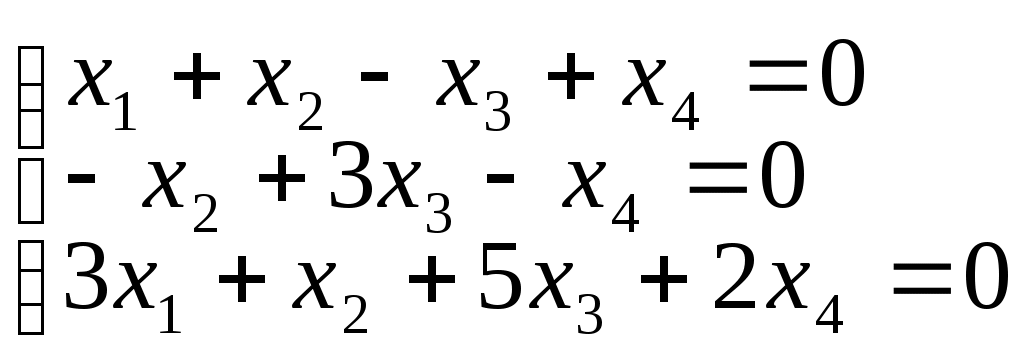 б)
б) 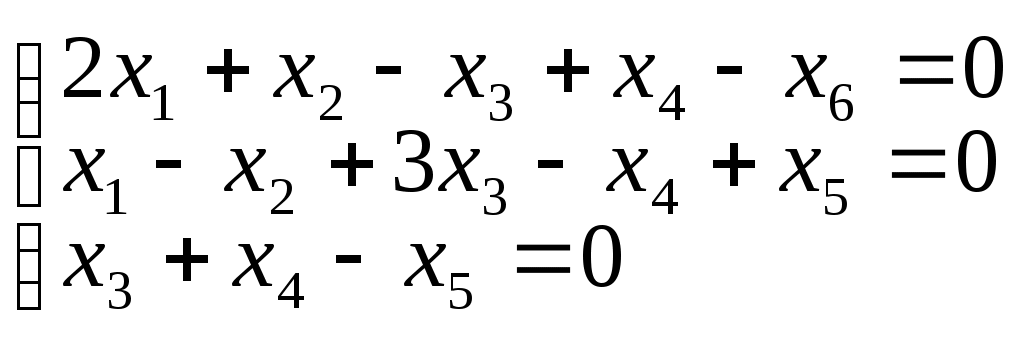
в)
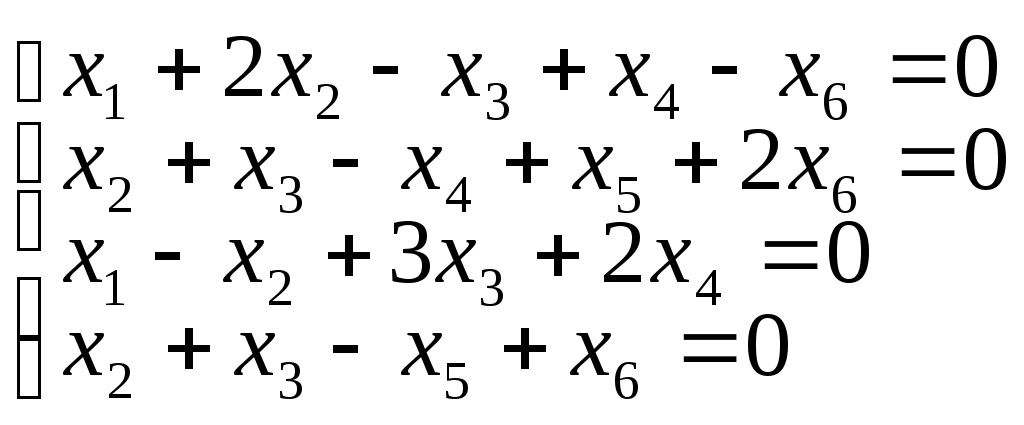 г)
г) 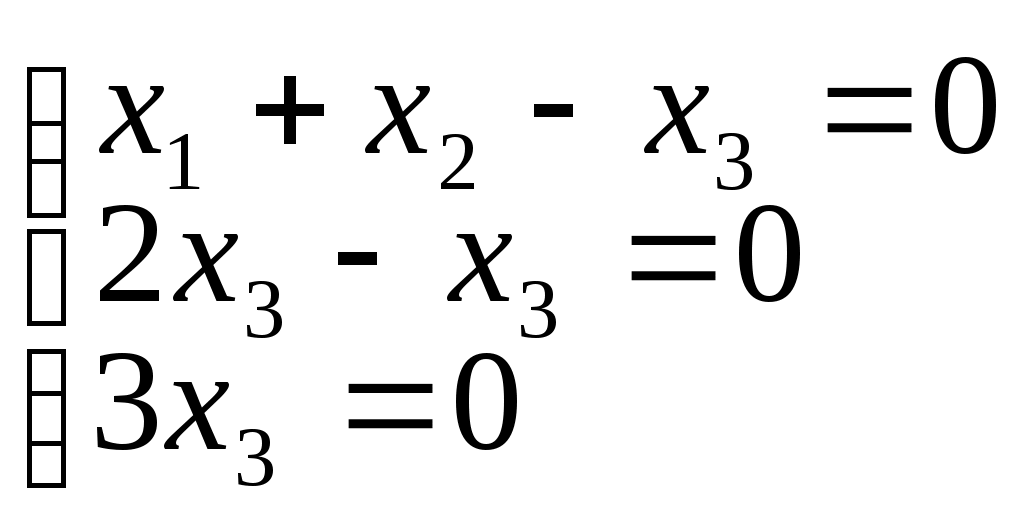
Практическое занятие №10
Решение однородных систем линейных уравнений.
1. Решить системы однородных линейных уравнений:
а)
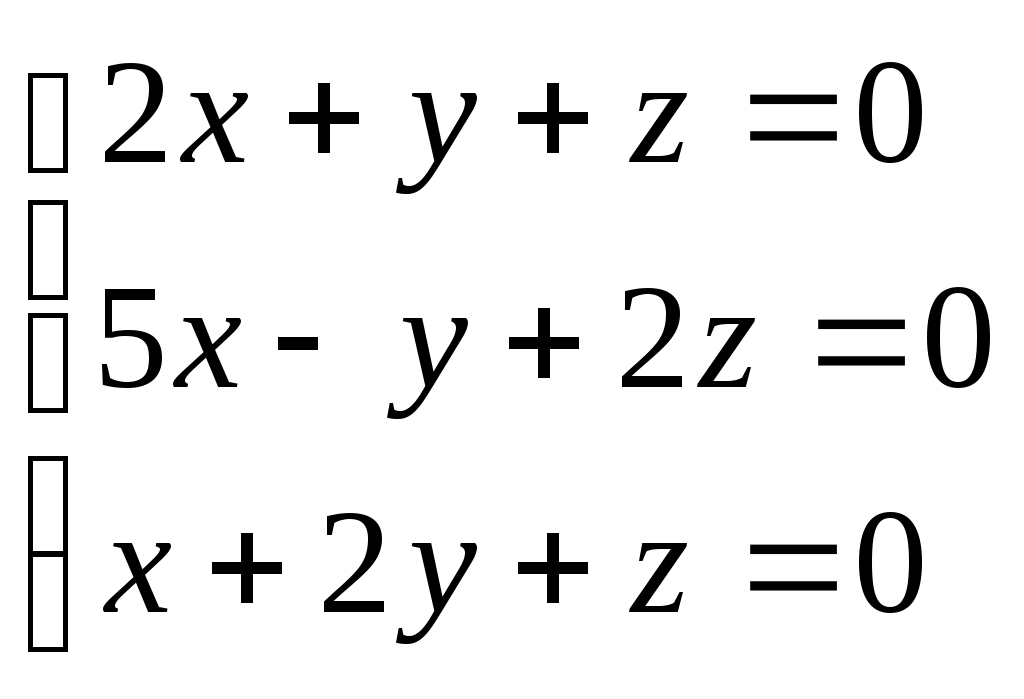 б)
б) 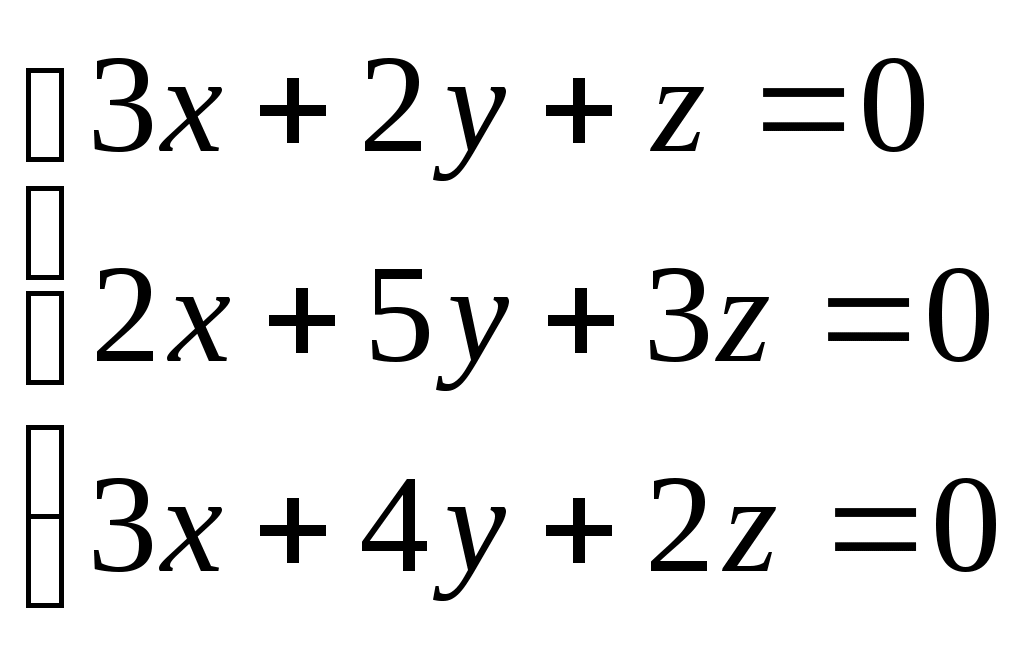
в)
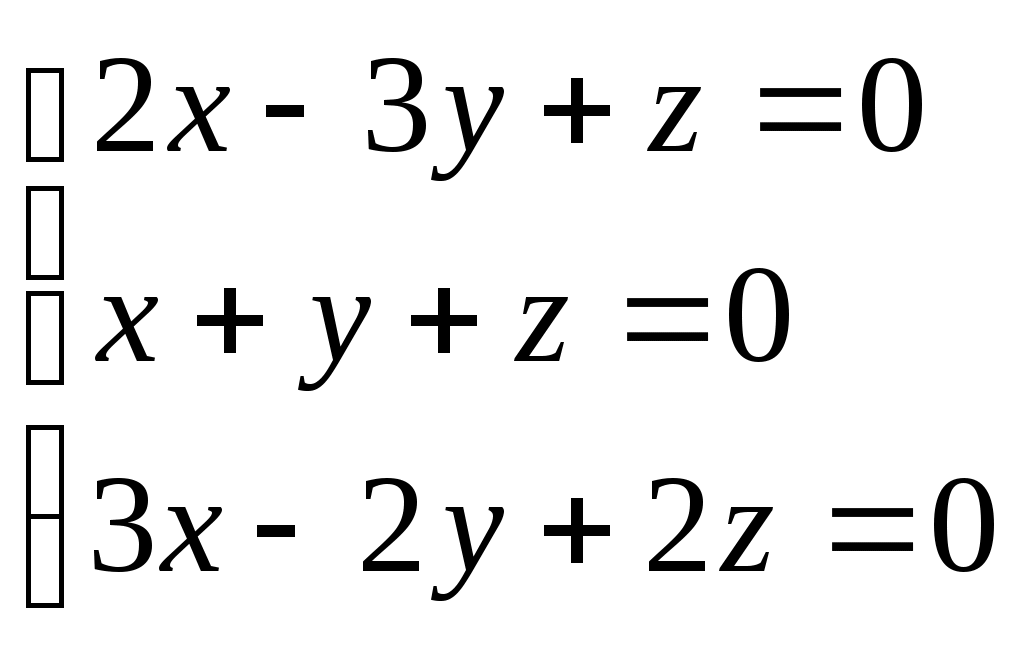 г)
г) 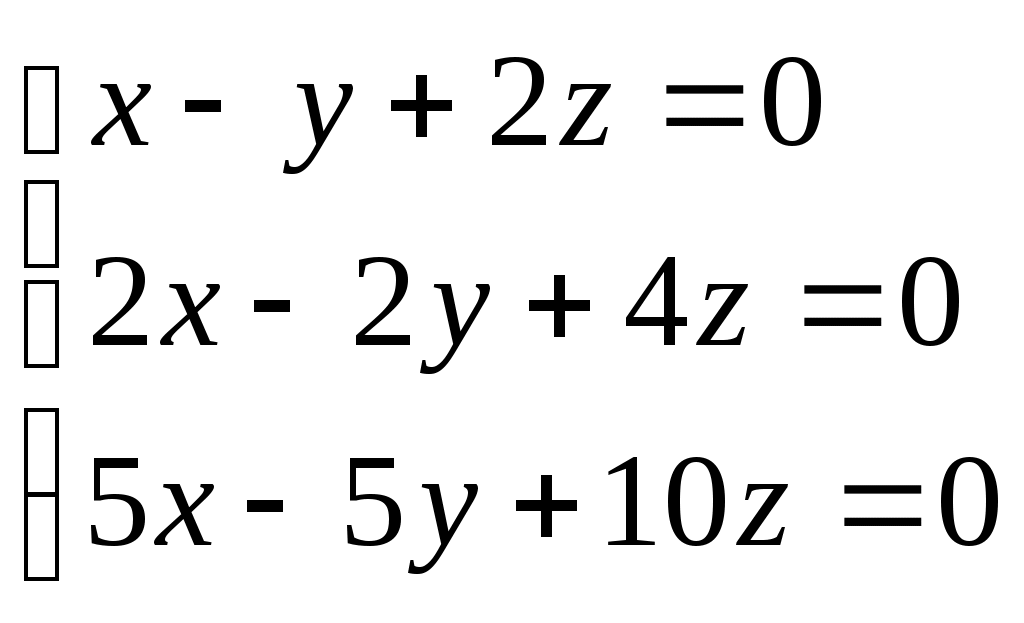
2. Доказать утверждения: а) если векторы Х и У являются решениями однородной системы, то их сумма также является решением данной системы; б) если вектор Х является решением однородной системы, то вектор
3. Докажите, что система не имеет нетривиальных решений:
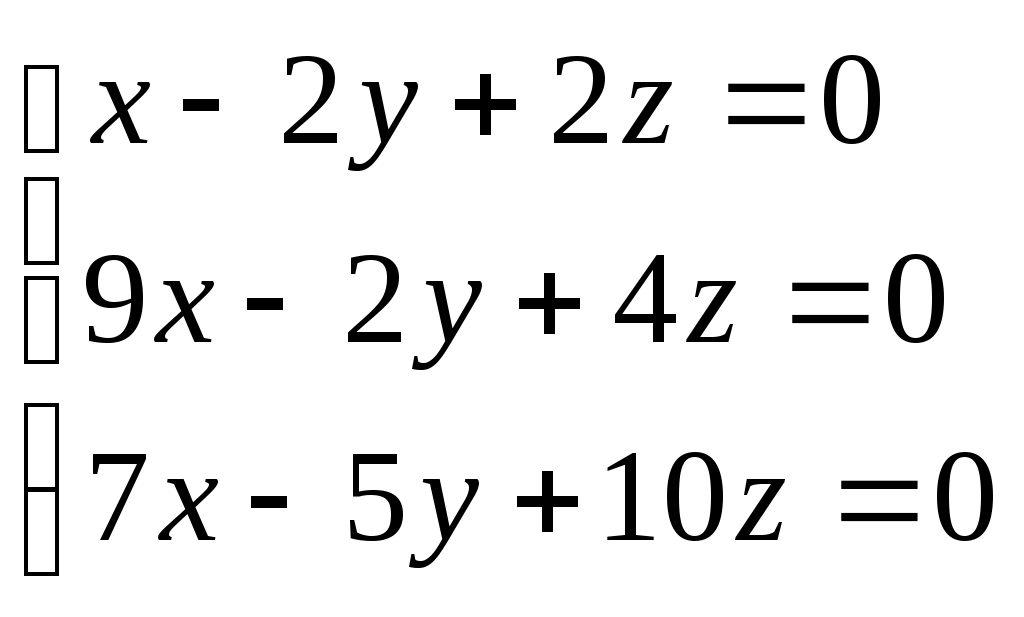
Практическое занятие №11
Контрольная работа №1 по темам «Понятия об основных алгебраических структурах», «Теория делимости в
кольце Z», «Матрицы», «Определители квадратных матриц», «Решение систем линейных уравнений».
Задание I. Выяснить, какую алгебраическую структуру образует:
1. <2Z, > , где x, у 2Z, х у =
2.
3. <2Z, +, •>
4.
+,+, •>
5.+, >, где x, у R+, х у = ху
6.{1}, >, где x, у R{1}, х у = x + y - xy
7., где "x, у Î R, х ° у = х + у - 1
8.8, , > где 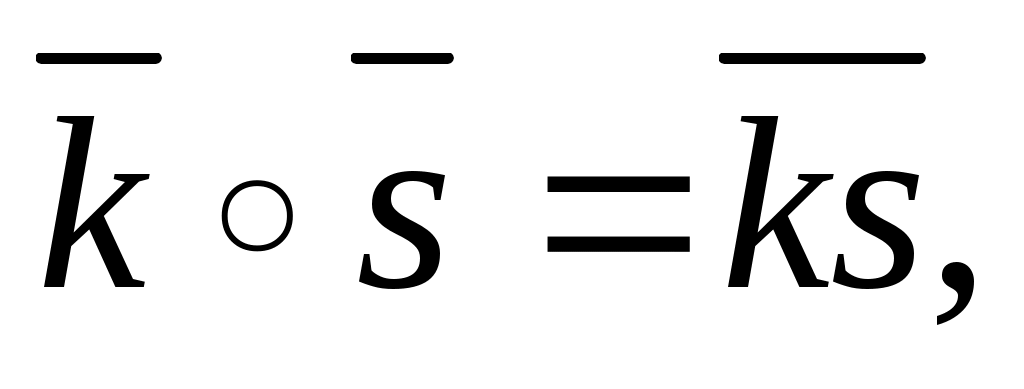

9.11, ,•>
10., где x y = 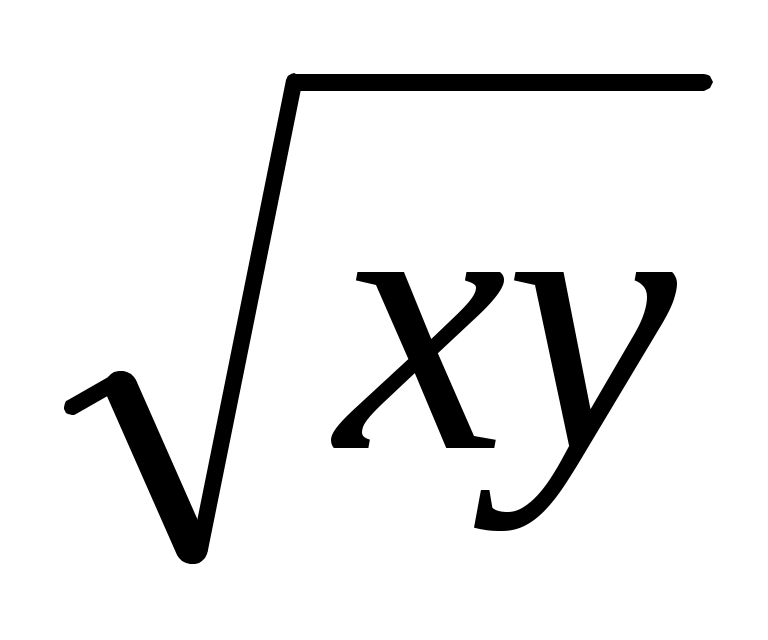
Задание II. Найти строчный ранг матрицы.
1.; 2.
; 3.
;
4.; 5.
; 6.
;
7.; 8.
; 9.
;
10.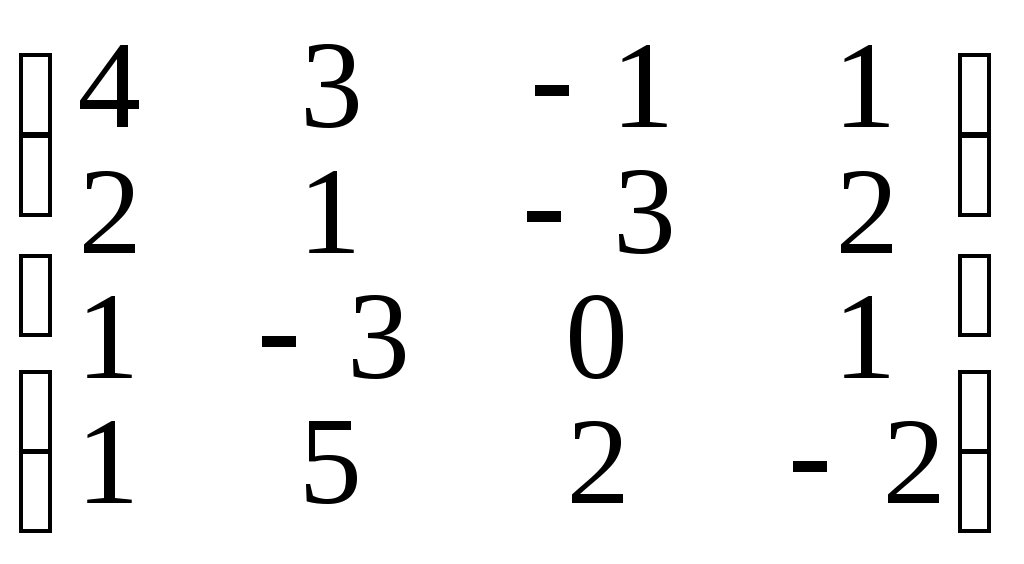
Задание III. Вычислить матрицу, обратную данной:
1.; 2.
; 3.
; 4.
; 5.
; 6.
; 7.
; 8.
; 9.
; 10.

Задание IV. Вычислить значение определителя:
1); 2)
; 3)
; 4)
5)
; 6)
;
7); 8)
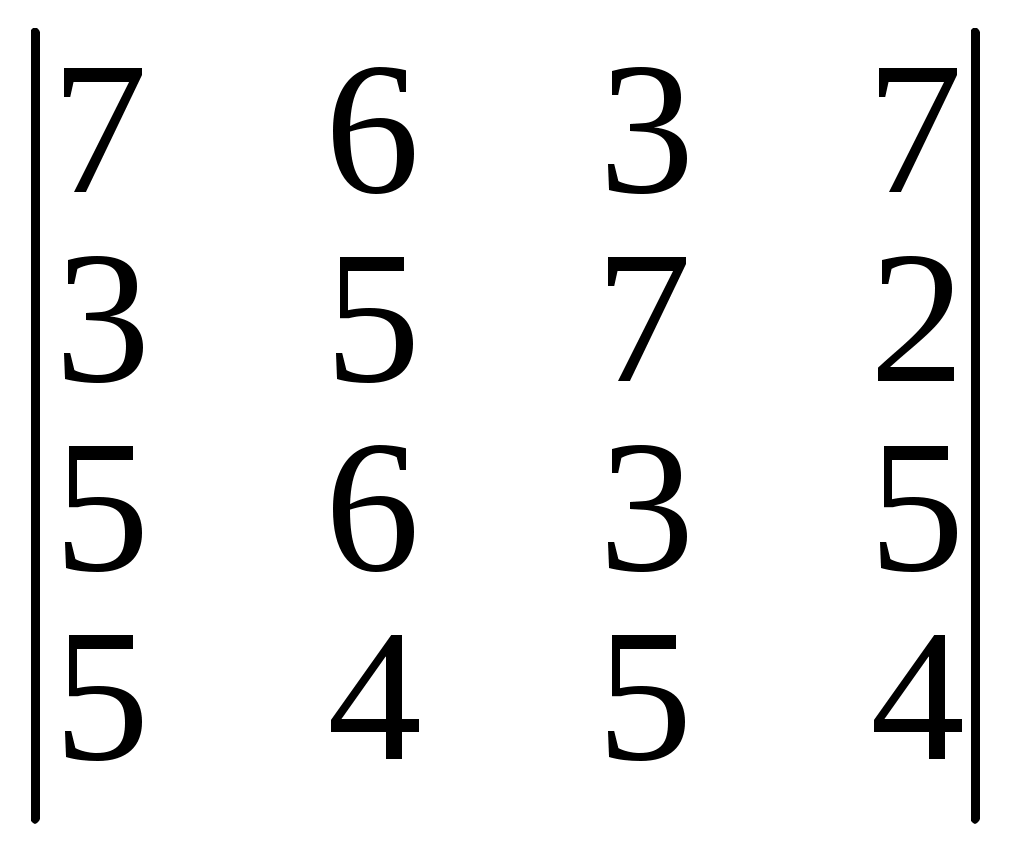
9); 10)
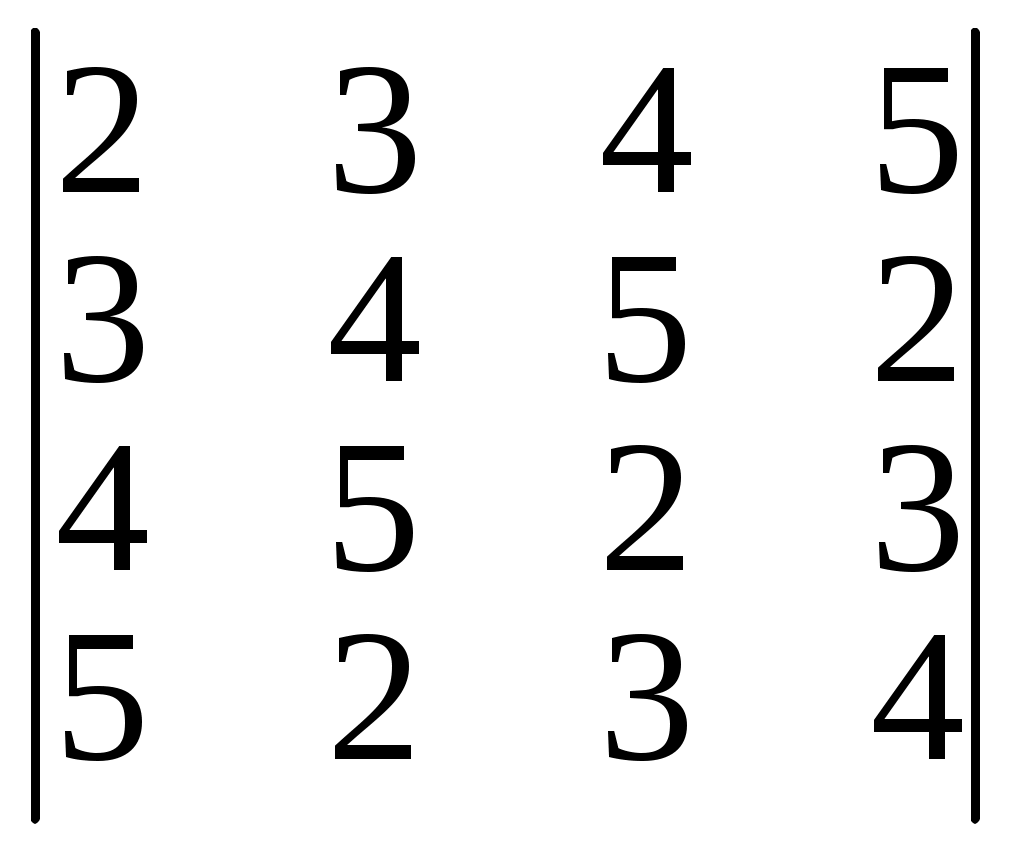
Практическое занятие №12
Алгебраическая форма комплексного числа.
Действия над комплексными числами в
алгебраической форме.
1. Построить точки (радиус-векторы), изображающие комплексные числа:
z1 = 2, z2 =-2i,
z3 = 1 + 2i, z4 =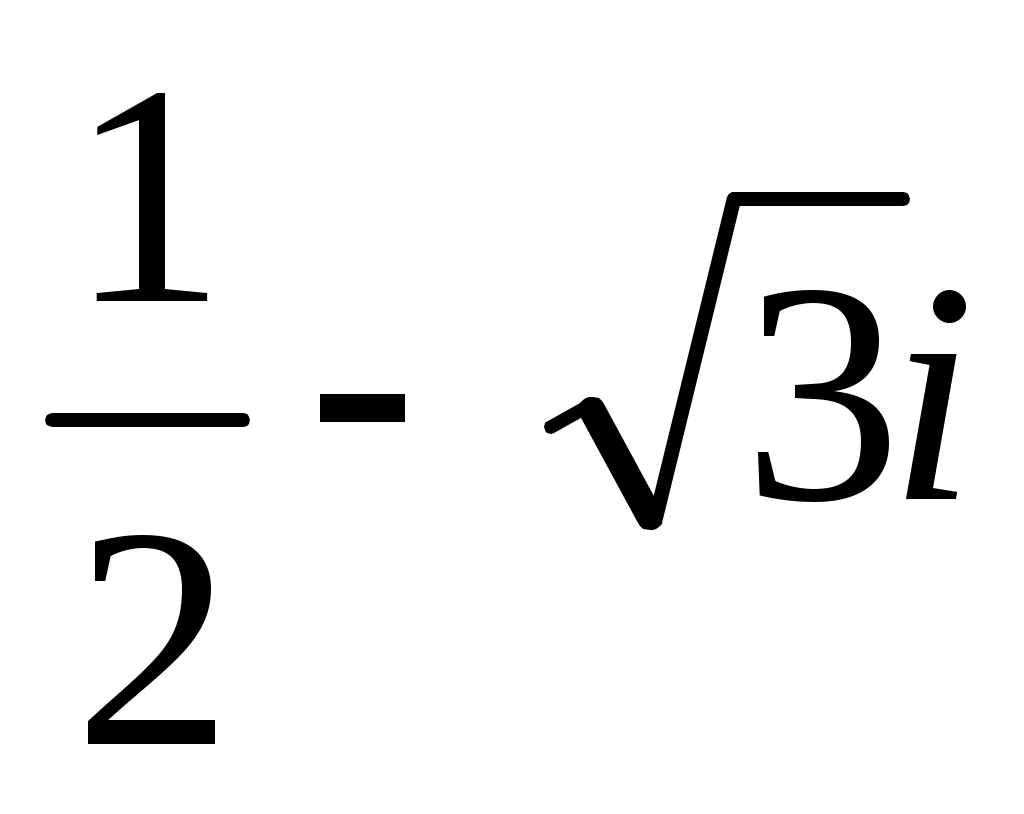
2. Построить векторы, изображающие сумму и разность комплексных чисел:
a) z1 = 2 – i, z2=l+3i;
б) z1 = -3 + 2i, z2 = 5 + I;
в) z1 = 2i, z2 = -3-4i
3. Выполнить указанные операции над комплексными числами в алгебраической форме.
a)б)
в) (1 – 2i)10
г)д)
е)
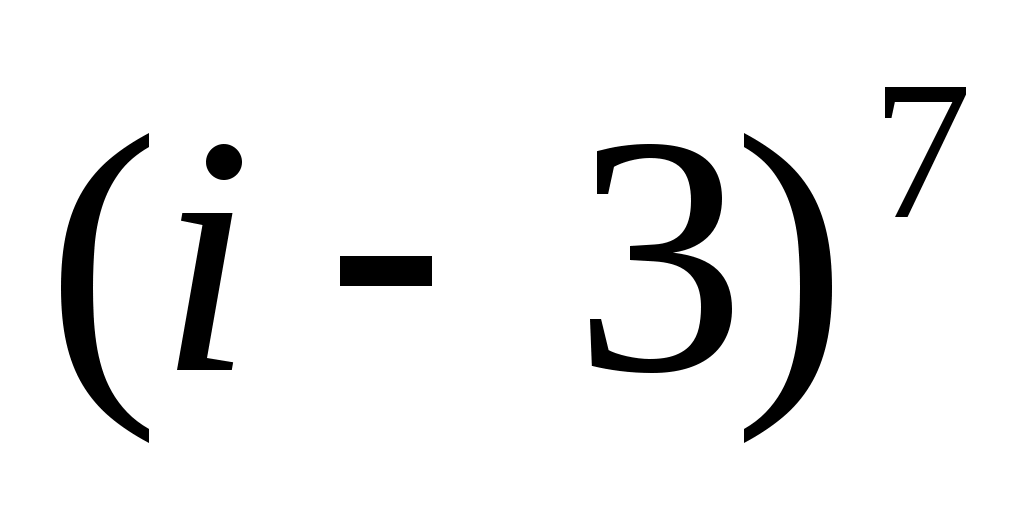
4. Доказать тождество: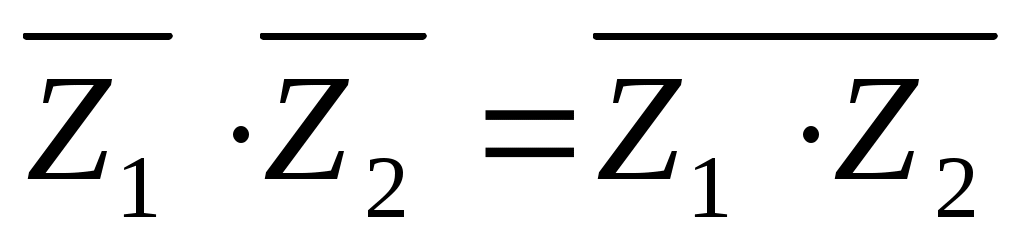
5. Доказать тождество: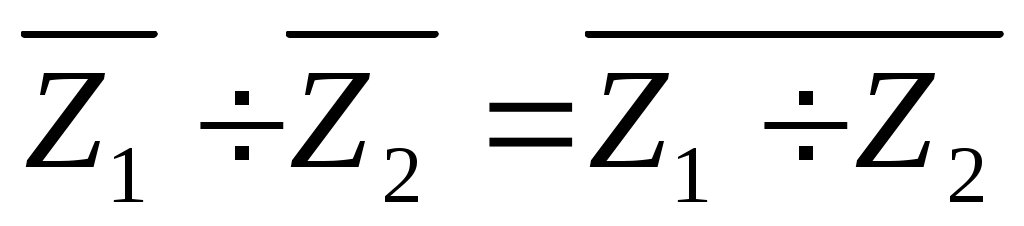
Практическое занятие №13
Тригонометрическая форма комплексного числа.
Действия над комплексными числами в тригонометрической форме.
1. Представить в тригонометрической форме следующие комплексные числа:
a) z = 3; b) z = -2; c) z = -i; d) z = -1 – i;
e) z = 3 + i; f) z = <3, -1>; g) z = <0, 5>; h) z = <-1, 1>
2. Записать в алгебраической форме следующие комплексные числа:
a)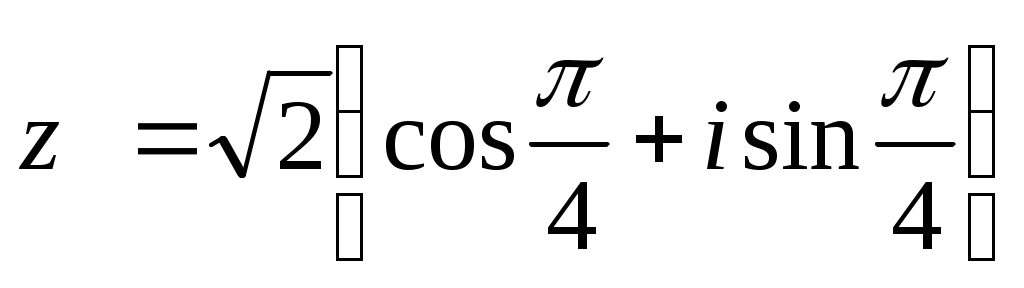
b)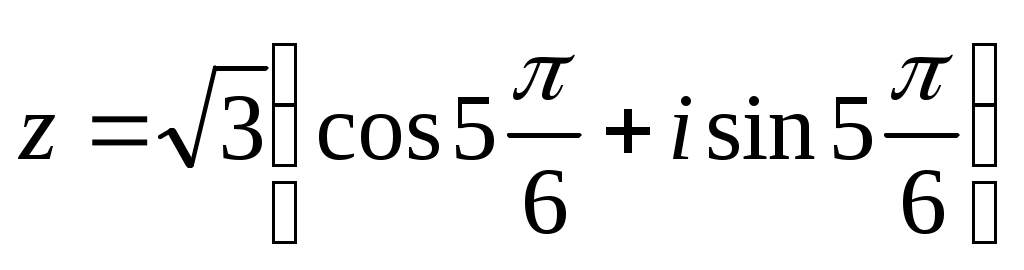
c)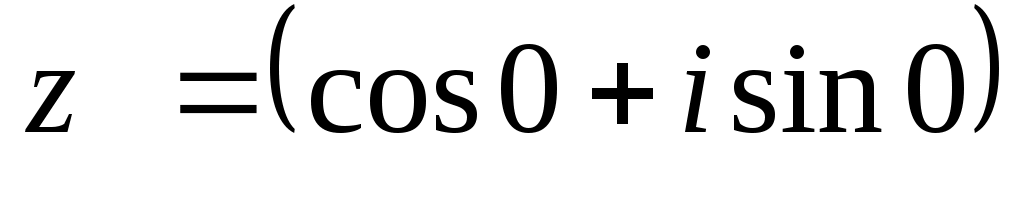
d)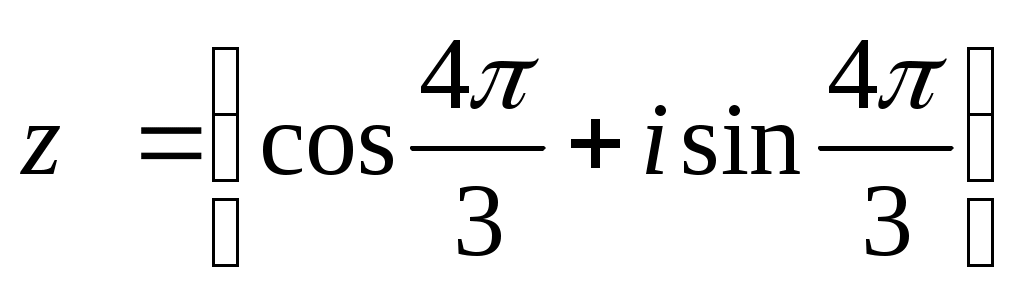
3. Выполнить указанные операции в тригонометрической форме.
a),
b)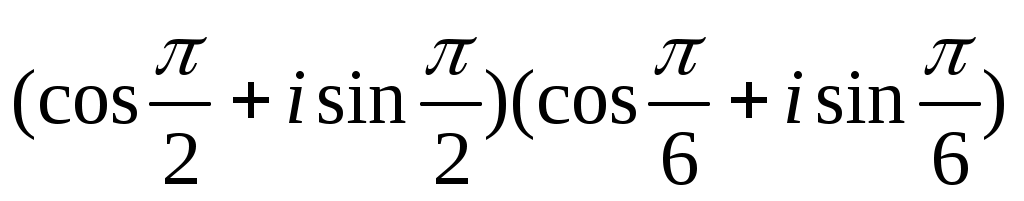
c), d)
,
e), f)
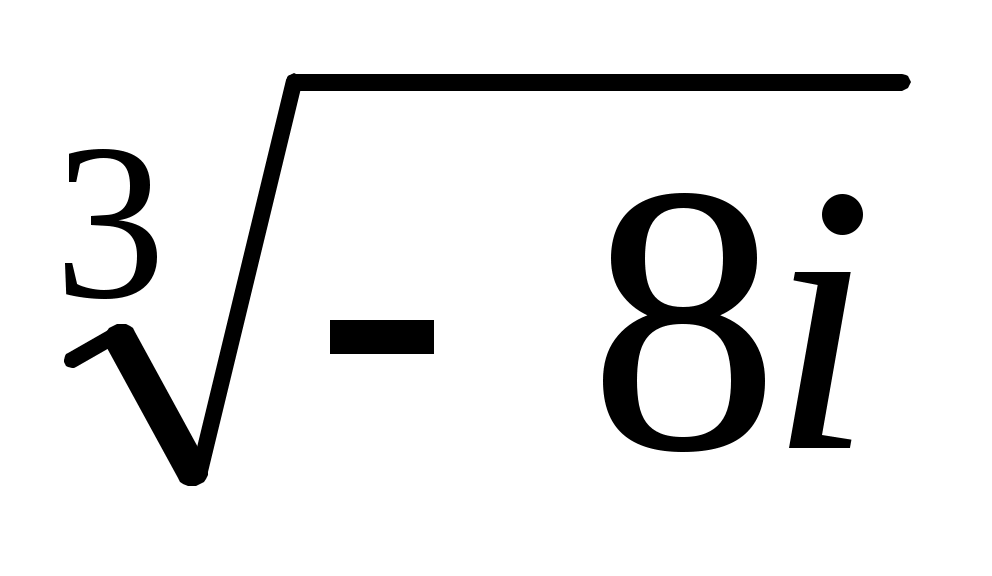
4. Найти геометрическое место точек, для которых
a) |Z| 3, b) |Z - 3i| < 1,
c) |Z + (1 - i)| > 4, d) |Z + 2i| + |Z – 4 + i| = 10,
e) arg z = /2, f) |Z - 4| + |Z – 3i| = 8.
Практическое занятие №14
Отношение делимости в кольце Z.
Свойства отношения делимости в кольце Z.
Деление с остатком в кольце Z.
Теорема о делении с остатком.
1. Доказать, что если (a/с)& (b/с) (a±b)/c
2. Доказать, что если (a/c)&(bZ) (аb)/с
3. Доказать, что если (а/b) => |а| > |b|
4. Доказать, что nZ n(n+1)/2
5. Разделить с остатком
а) - 145 на 13 б) 356 на -27 в) - 1248 на 325
6. Доказать, что при nZ (n3 + 5n)/6
7. Доказать, что nZ (n3 + 11n)/6
8. Доказать, что nZ (n3 + n)/2
9. При каких nZ число n2 - 1 делится на 3?
10. Доказать, что nZ n2(n2-1 )/4
11. Доказать, что nZ (n5-n)/5
12. Доказать, что если n = 2k + 1, то (n2-l)/8
13. Доказать, что ни при каком nZ число n2+1 не делится на 3
Практическое занятие №15
Наибольший общий делитель целых чисел и его свойства. Способы нахождения наибольшего общего делителя. Алгоритм Евклида. Линейное представление наибольшего общего делителя.
1. Доказать, что если а = bq +r, где а, b, r 0, то (а, b) = (b, r).
2. Доказать, что если (а1, а2) = d & (d1, а3) = d2 &…& (dn-2, an) = = dn-1 => (a1,a2, an) = dn-1.
3 Применяя алгоритм Евклида, найти НОД(а, b), если:
а) а = 6188, b = 4709.
б) а = 3164, b = 142.
в) а = 10248, b = 2142.
г) а = 4562, b = 356.
д) а = 1524, b = 240.
Практическое занятие №16
Взаимно простые числа и их свойства.
Наименьшее общее кратное целых чисел и его свойства. Способы нахождения наименьшего общего кратного.
1. Доказать, что если d = (a, b) => (а / d, b / d) = 1.
2. Доказать, что если ((аb) /с) & (а, с) = 1) => (b/с).
3. Доказать, что если (с /а) & (с /b) => (с /ab).
4. Доказать, что если ((а, с)=1) & (b, с) = 1) => (а b, с) = 1.
5. Доказать, что [а, b] = ab/(а, b)
6. Доказать, что [a/k, b/k] = [а, b] / к, где к 0, kZ
7. Доказать, что если
( [а1, а2] = m1) & ([m1, а3] = m2) &... &([mn-2,аn] = mn-1) => [а1а2...аn]=mn-1
8. Вычислить НОК [а, b], используя формулу:
[а, b] = ab/(а, b)
а) а = 84, b = 36
б) а = 72, b = 22
в) а = 124, b = 32
г) а = 244, b=18
9. С помощью решета Эратосфена выделить все простые числа от 2 до 100.
10. Выяснить, какие из чисел
197, 443, 739, 447, 729, 809
будут простыми, какие составными.
11. Найти каноническое разложение чисел:
а) n = 34862
б) n = 126356
с) n = 342124
12. Найти все делители чисел 640, 426, 188.
13. Найти НОД (а, b) и НОК [а, b], используя каноническое разложение.
а) а =124, b = 36, б) а = 328, b = 49,
в) а = 254, b = 52, г) а =1244, b = 356.
Практическое занятие №17
Отношение делимости в кольце P[x].
Деление с остатком в кольце P[x].
1. Выяснить, делится ли многочлен f(x) на многочлен g(x) в соответствующем кольце, если:
а) f(х) = 10х5 - 4х4 + 2х3-12 g(x) = х7-3х+1 (Z[x])
б) f(х) =х6 -
х4 +
х2-
g(x) =
х2 -
х +
(Z15[x])
в) f(x) = (l+5i)x3- x2+ 2i g(x) = 2ix2 - 8i (C[x])
2. При каких условиях многочлен f(x) делится на многочлен g(x)?
а) f(х) = 8x5 - 3х4 + ах + b на g(x) = x3 +2х -1 в кольце Z[x]
б) f(х) =x4-
x2 +
на g(x) =
х2-
х +
в кольце Z7[х]
в) f(x) = 3ix4 +(a)x2 + b на g(x) = 3х2 - (l+i)x + 2i в кольце С[х]
3. Доказать, что если f(x) /g(x), то
1) либо f(x) = 0,
2) либо cm f(x) cm g(x).
4. Найти сумму, разность и произведение многочленов.
а) f(x) = 4х5 + 3х3 + 2х + 8 и g(x) = х4 - 10х + 1 из кольца Z[x]
б) f(x) =х4 +
х3 -
х -
и g(x) = х5 -
х4 +
из кольца Z13[x]
в) f(x) = (l-2i)x3 + 2ix2 - 4i+l и g(x) = 5ix2 + 2x-i из кольца С[х]
5. Определить степень суммы и произведения многочленов
а) f(х) = 3х7 + 2x3 + х3 + 5 g(x) = x8 - 2х + 7 в кольце Z[x]
б) f(х) =х15 + х5 - х3 +
g(x) =
x2 - х +
в кольце Z11[x]
в) f(x) = 3ix7 + (2 - 6i) x2 + 8 g(x) = 7ix3 + 2ix + 1 в кольце С[х]
6. Доказать, что множество многочленов, степень которых не превосходит 5, образует кольцо и линейное пространство относительно соответствующих операций. Указать базис и размерность этого линейного пространства.
7. Выяснить будет ли множество Р[х] полем относительно операций сложения и умножения многочленов.
Практическое занятие №18
Наибольший общий делитель многочленов. Способы нахождения наибольшего общего делителя. Линейное представление наибольшего общего делителя.
1. Дать определение НОД(f, g) и HОK(f, g).
2. Доказать, что если f(x) = g(x)h(x) + r(x), где cm r(x) < cm g(x), то (f, g) = (g, r)
3. Доказать, что (f,g) = rn(x), где rn(х) - последний, неравный нулю, остаток в алгоритме Евклида.
4. Доказать, что если d = (f, g), то u, v P[x]:
d(x) = f(x)u(x) + g(x)v(x).
5. Доказать, что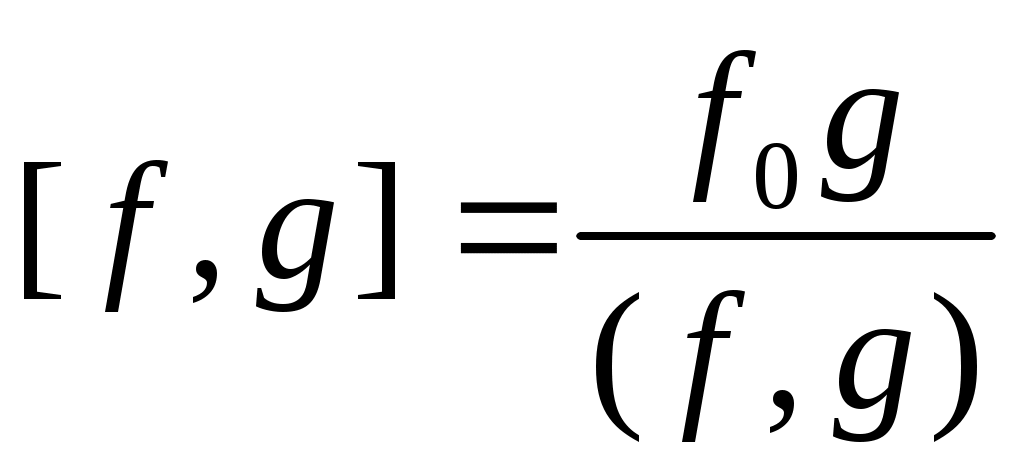
6. Разделить с остатком многочлен f(x) на g(x):
а) f(x) = 2x4 - 4x3 + 4x2 - 6, g(x) = x2 - 3x - l, f, gZ[x]
б) f(x) =x4 +
x2 -
, g(x)=x3 -
x -
, f, gZ7[x]
в) f(x) = (10 + 5i)x4 - (15 + 5i)x2 + (10 - 5i), g(x) = (2 + i)x2 - 3x + i, f, gC[x].
Практическое занятие №19
Наименьшее общее кратное многочленов. Способы нахождения наименьшего общего кратного многочленов.
1. Найдите делитель, если известно делимое, неполное частное g(x) и остаток r(х):
a) f(х) = 2х5 + 3х4+ 2х3 + 1, g(x) = x2 + 3x + l, r(x) = 63x + 25, f, g, rZ[x]
b) f(x) = x5 - 2x4 - х3 - 7x2 - 5x – 4, g(x) = x3 - 3x2 - l, r(x) = -4x + 5, f, g, rQ[x]
c) f(x) =х2 +
x +
, g(x) = x2 -
, r(x) =
x +
, f, g,Z10[x]
2. Найти (f, g) и [f, g] многочленов:
a) f(x) = x3 + 4x - 3, g(x) = x4 + x3 - x2 + x - 2, f, gZ5[x]
b) f(x) = x4 + 2x3 + 2x2 + 2x + 2, g(x) = x3 + 3x2 + 2, f, gQ[x]
c) f(x) = x5 +(l - i)x4 +x3–ix - i, g(x) = x4 - ix3 –(1-i)x2 –x+l, f,gC[x]
3. Спомощью алгоритма Евклида найти линейное представление d(x) = (f(x), g(x))
a) f(x) = 4x4 - 2x3 - 16x2 + 5x + 9, g(x) = 2x3 - x2 - 5x + 4, f, gQ[x]
b) f(x) = x5 + 3x4 + x3 + x2 + 3x + l g(x) = x4 + 2x3 + x + 2, f, gQ[x]
4. Докажите, что если (fg)/h, причем (f,h)=l, то (g/h).
Практическое занятие №20
Корни многочлена. Деление многочлена на двучлен. Схема Горнера. Применение схемы Горнера к решению практических задач.
1. Выполнить деление с остатком:
а)на
;
б)на
;
г)на
;
д)на
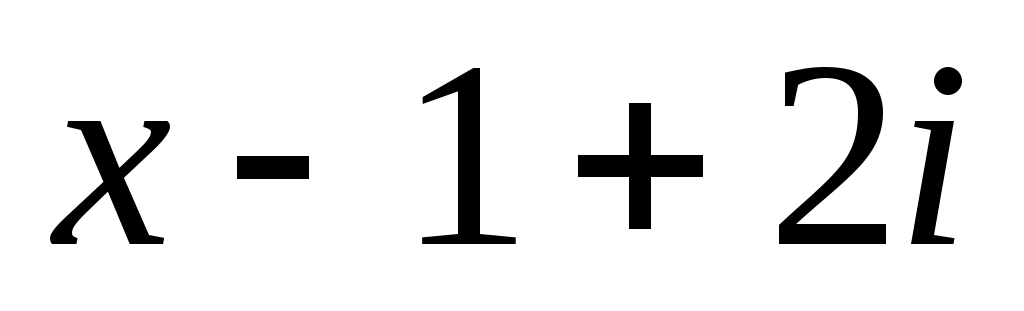
2. Пользуясь схемой Горнера, вычислить:
а);
б);
3. Пользуясь схемой Горнера, разложить многочленпо степеням
:
а);
б);
в);
г)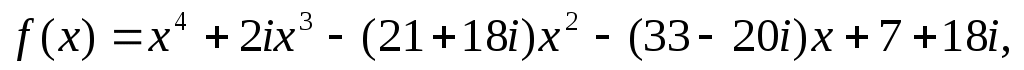
.
Практическое занятие №21
Приводимые и неприводимые над данным полем многочлены. Формулы Виета.
1. Доказать, что если f(x) и g(x) неприводимые многочлены над полем Р, степени больше нуля и f(x)/g(x) => f(x)=c g(x), где сР.
2. Доказать, что многочлен f(x) P[x] тогда и только тогда не делится на неприводимый многочлен р(х) над полем Р, когда (f, p) = c.
3. Доказать, что если произведение многочленов f(x) и g(x) делится на неприводимый многочлен над полем Р, то (f(x)/р(х)) (g(x)/р(х))
4. Доказать, что если f, g P[x] & (f, g) = c, то эти многочлены не имеют общих корней в поле Р.
5. Составить нормированный многочлен наименьшей степени над полем С, имеющий простой корень (-1) и двукратный корень (1-i)
6. Составить нормированный многочлен наименьшей степени над полем R, меющий простой корень (2) и двукратный корень (1 + i).
7. Над какими из полей Q, R или С приводимы многочлены:
a) f(x) = x2 - 4x - 2
б) f(x) = 3x2 - 2x + 4
в) f(x) = x3 - x2 + x + l
г) f(x) = 3x - 6
д) f(x) = х3 – 1
8. Найти кратность корня () многочлена f(x):
а) f(x) = x 5 - 5х 4 + 7х 3 - 2х2 + 4х - 8, =2
б) f(x) = x5 + 7x4 + 16x3 + 8x2 - l6x - 16, =-2
в) f(x) = x6 + 2х5 + 4х4 + 4х3 + 5х2 + 2х - 2, =-1
г) f(x) = x5 - 4х4 - 6х2 + 16x2 + 29 x + 128, = 3
Практическое занятие №22
Сопряженность комплексных корней многочлена с действительными коэффициентами. Неприводимые многочлены над полем действительных чисел.
1. Разложить многочлены на неприводимые многочлены над полями Q, R и С.
a) f(x) = x4 + 2x3 + x2 - l
б) f(x) = x4 - x3 - 3x2 + 5x - 10
в) f(x) = х4 - 2x3 + 4х2 + 2х – 5
г) f(x) = x3 – 6ix + 4 – 4i
д) f(х) = х3 - 12х + 16
е) f(x) = х3 + 9х2 + 18х + 28
ж) f(x) = х3 - 6х2 + 57х - 196
з) f(x) = x3 - 6x2 + 21x - 5
и) f(x) = х4 + х3 - 11х2 - 5х + 30
к) f(x) = 4х5 + 12х4 + х3 + 6х2 + 10х - 3
л) f(x) = 3х5 + 17х4 - 36х3 + 38х2 - 20х - 8
м) f(x) = 6х6 - х5 - 23х4 - х3 - 2х2 + 20х - 1
н) f(x) = 2х5- 15х3 + 21х - 28
о) f(x) = 3х6 - 20х4 + 30х2 - 20х + 23
2. Найти все корни многочлена:,
зная, что числоявляется его двукратным корнем.
3. Доказать, что любой многочлен нечетной степени имеет хотя бы один действительный корень.
Практическое занятие №23
Многочлены над полем рациональных чисел и кольцом целых чисел. Целые и рациональные корни многочленов с целыми коэффициентами. Неприводимые многочлены над полем рациональных чисел. Критерий неприводимости Эйзенштейна.
1. Докажите неприводимость многочленов
а);
б);
в)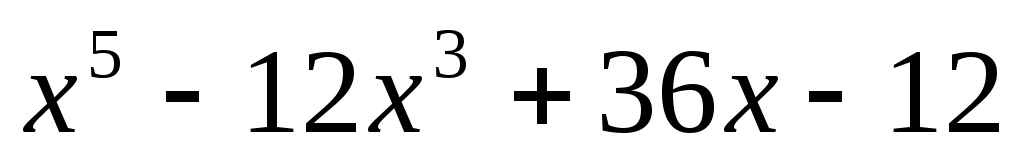
в кольце Q(x).
2. Найдите все рациональные корни уравнения:
а);
б);
в);
г);
д);
е).
3. Из чего следует единственность разложения на множители в кольце многочленов с рациональными коэффициентами?
4. Сформулируйте и докажите критерий Эйзенштейна.
Практическое занятие №24
Решение уравнений третьей степени в радикалах.
1. Решить уравнения методом Кардано:
а);
б);
в).
2. Непосредственно из формулы Кардано вывести, что многочленимеет кратные корни тогда и только тогда, когда его дискриминант равен нулю.
3. Пользуясь формулой Кардано, найдите с точностью до 0,01 действительный корень уравнений:
а);
б).
Практическое занятие №25
Решение уравнений четвертой
степени в радикалах.
1. Решить уравнения четвертой степени методом Феррари:
а);
б);
в);
г)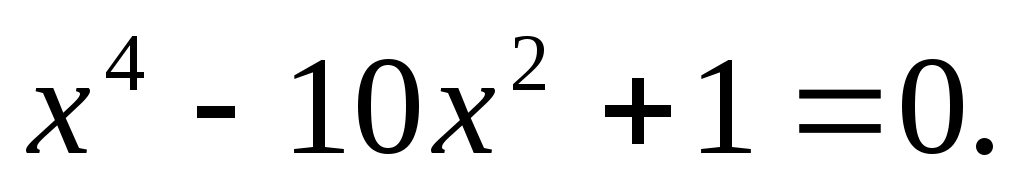
2. Решить уравнения четвертой степени методом Феррари, проверить правильность решения, найдя корни другими способами.
а);
б);
в);
г).
Практическое занятие №26
Методы решения алгебраических
уравнений высших степеней от
одной переменной.
1. Составить уравнение 6-й степени, имеющее корни:.
2. Найти сумму квадратов корней уравнения.
3. Чему равен показатель кратности корня:
а) 2 для многочлена;
б) –2 для многочлена.
Практическое занятие №27
Контрольная работа №2 по темам «Комплексные числа», «Приводимость многочленов над полями», «Решение алгебраических уравнений высших степеней».
Задание I. Решить систему линейных уравнений методом Гаусса.
1)2)
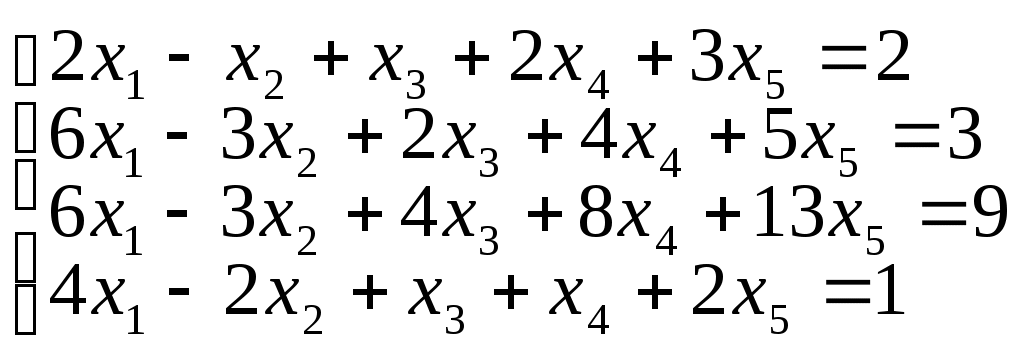
3)4)
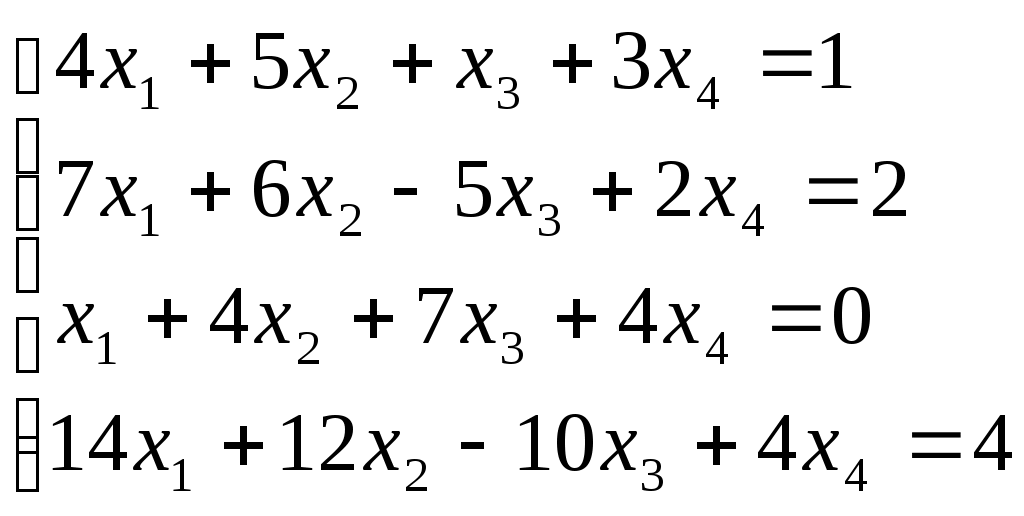
5)6)
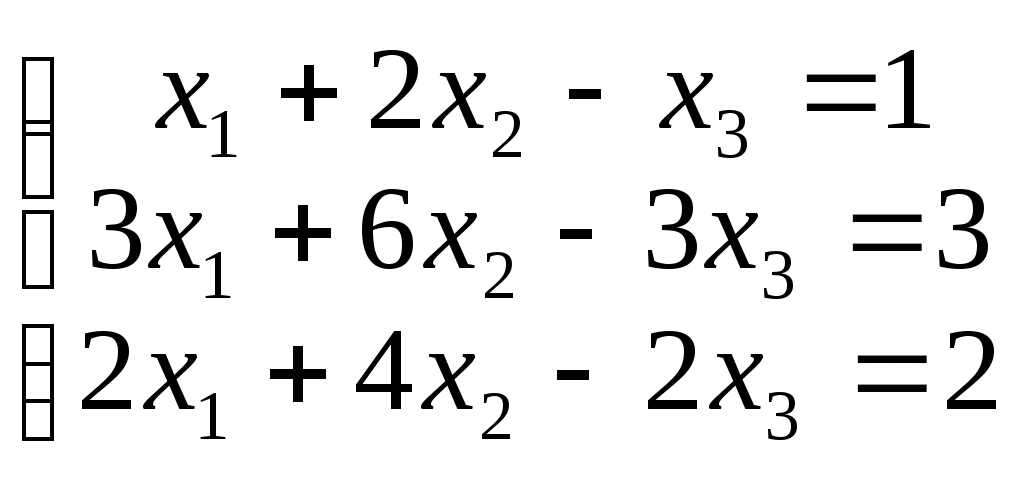
7)8)
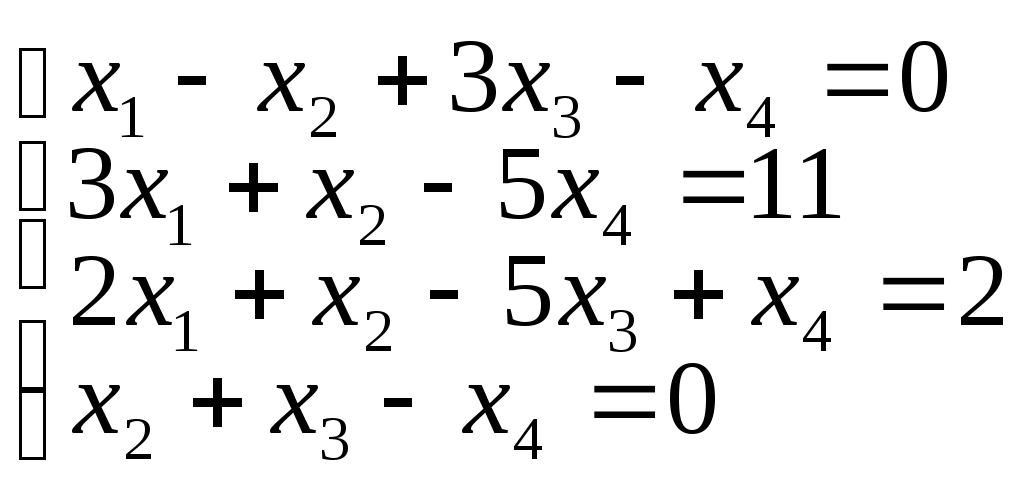
9)10)
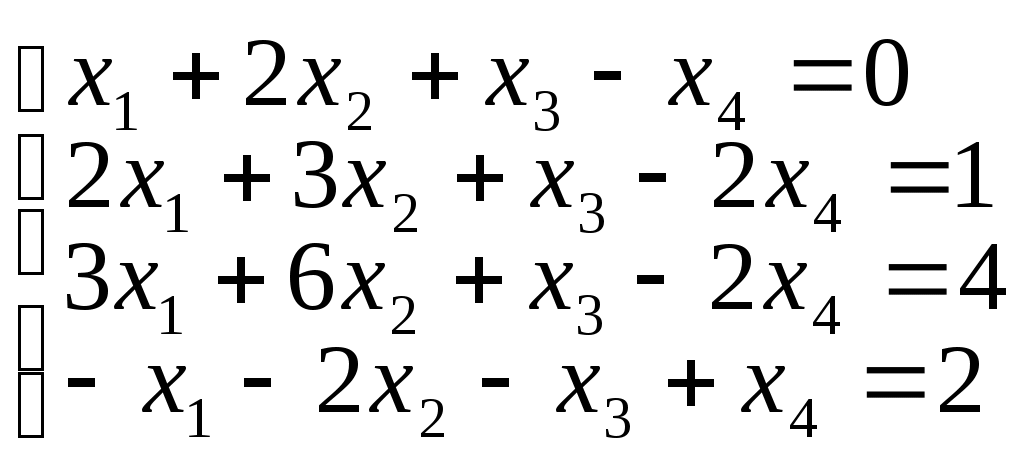
Задание II. Решить систему линейных уравнений матричным методом и методом Крамера.n = 1, 2, 3,…10
Задание III. Выполнить указанные операции над комплексными числами.
1); 2)
;
3); 4)
;
5); 6)
;
7); 8)
;
9); 10)
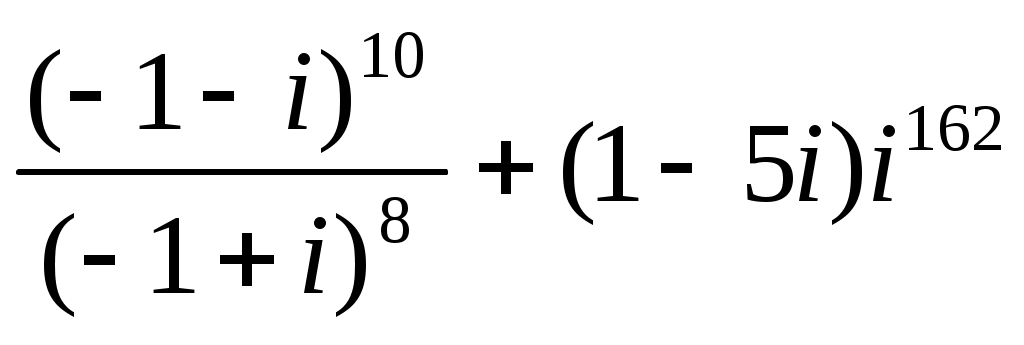
Задание IV. Записать в тригонометрической форме комплексные числа:
1)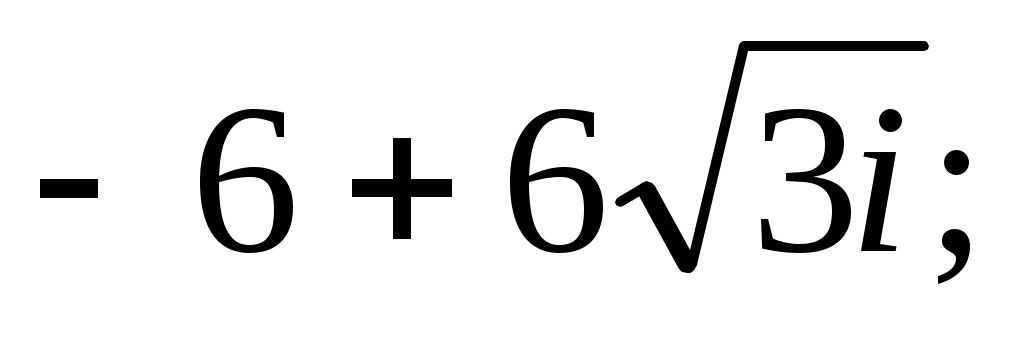
;
2)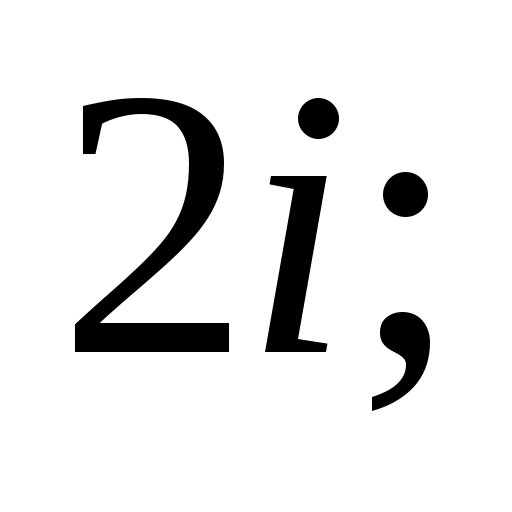
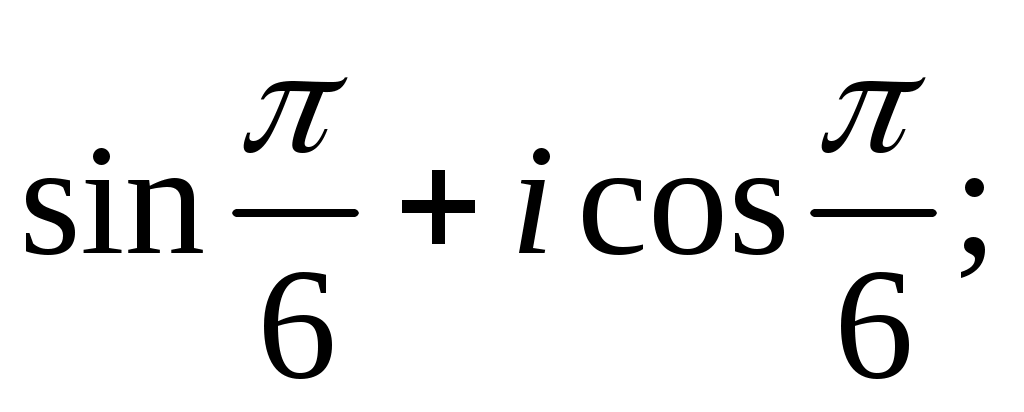
3)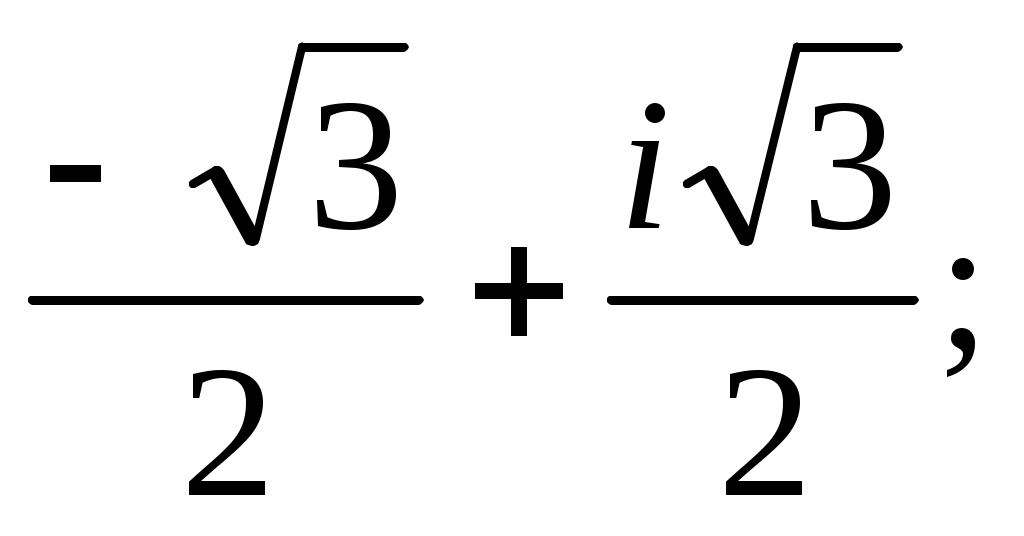
;
4)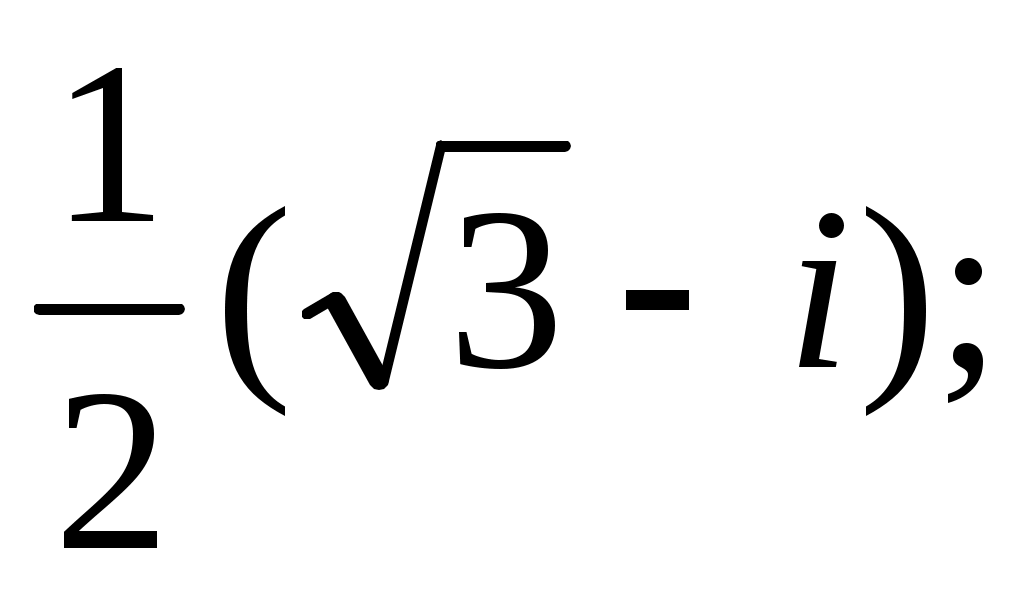
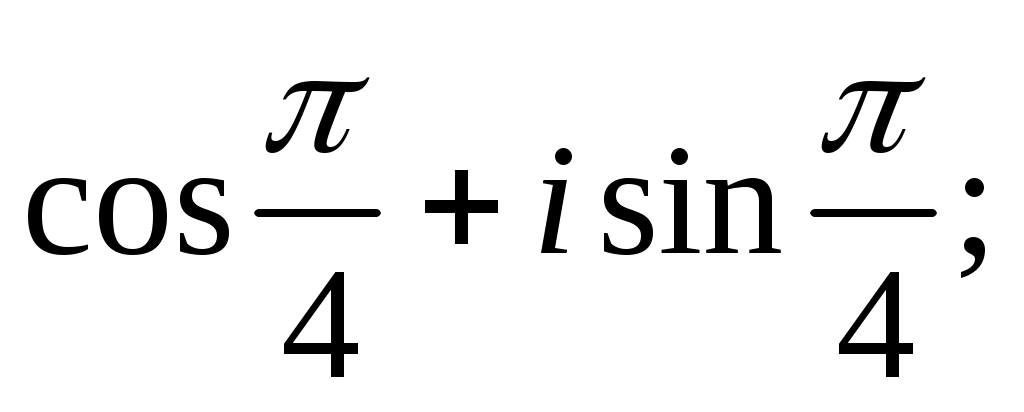
5)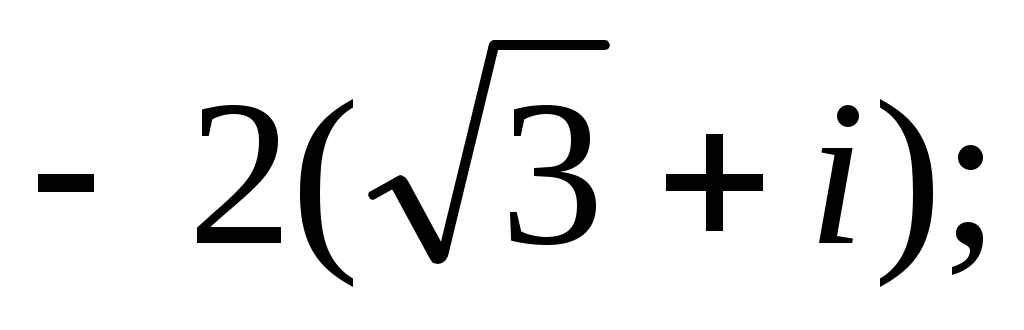
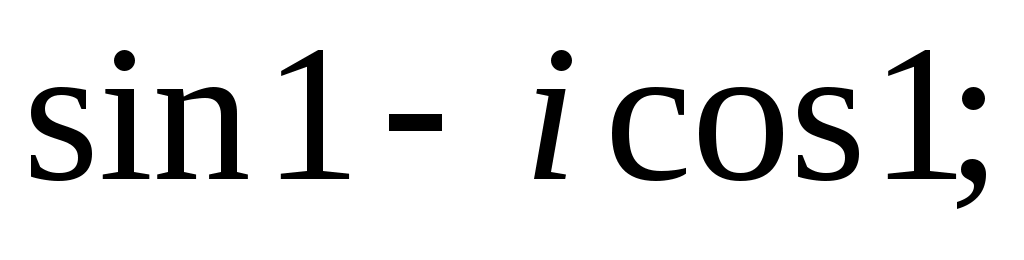
6)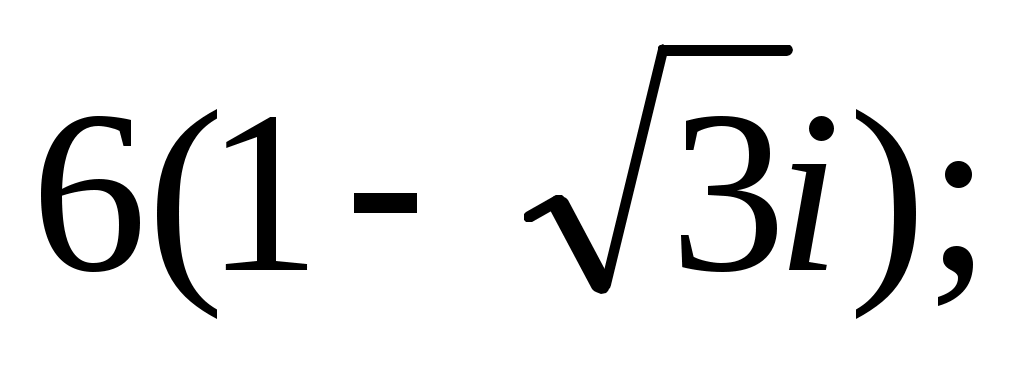
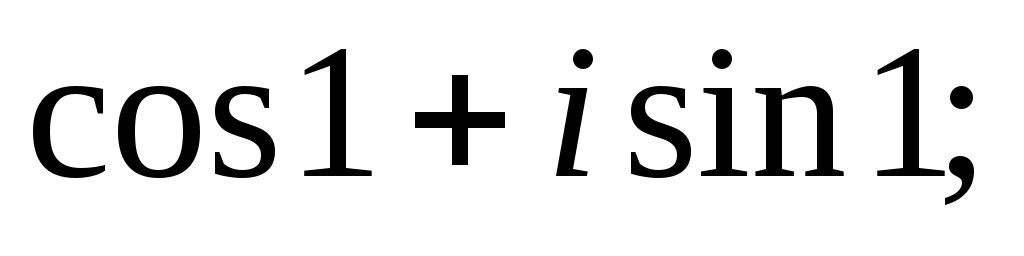
7)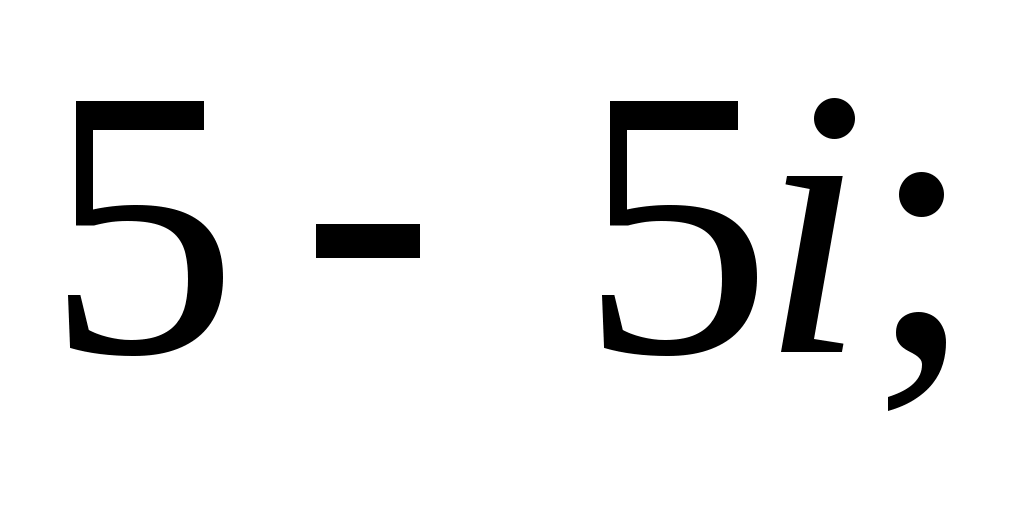
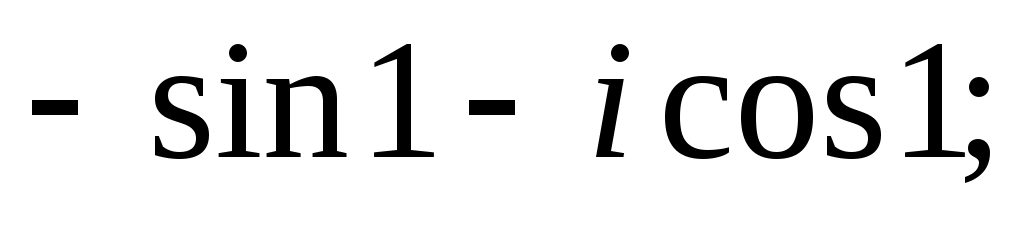
8)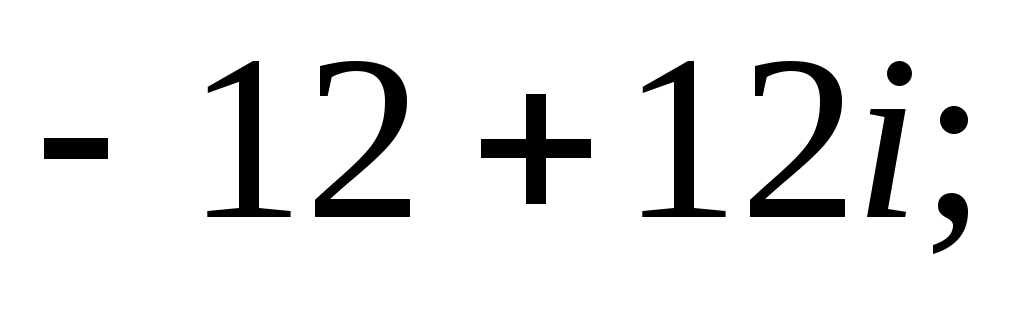
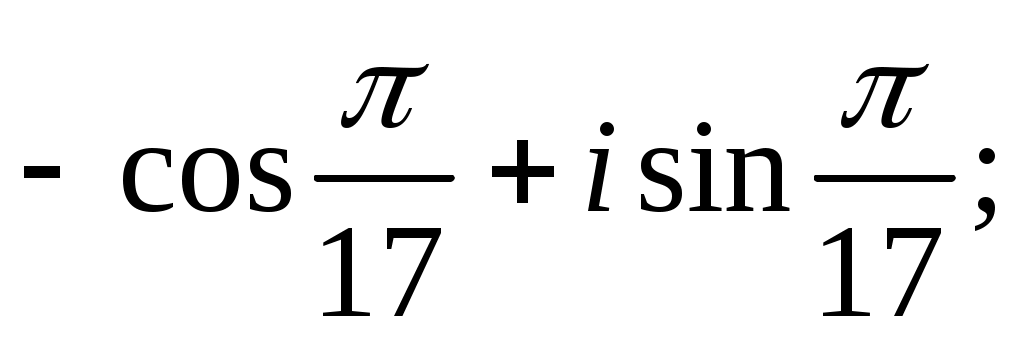
9)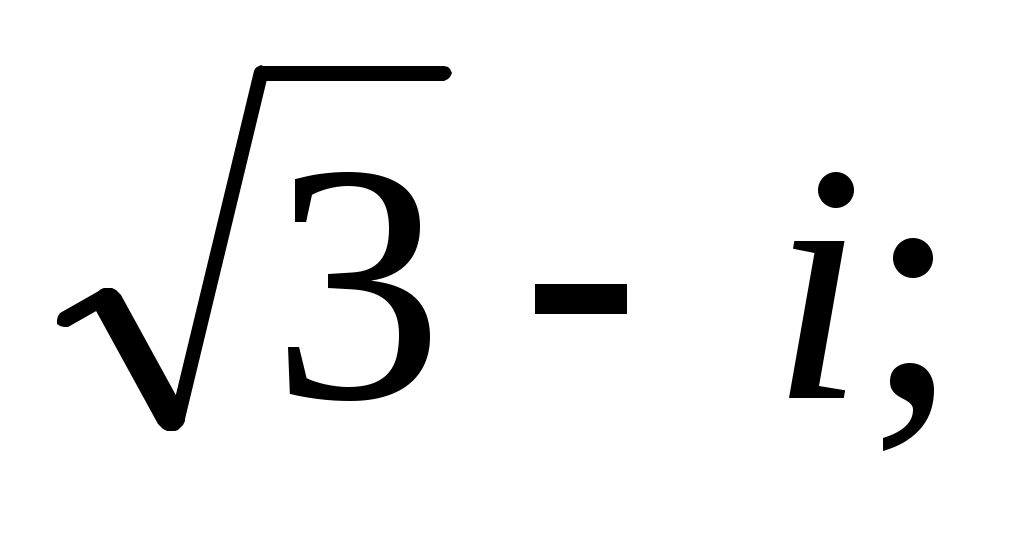
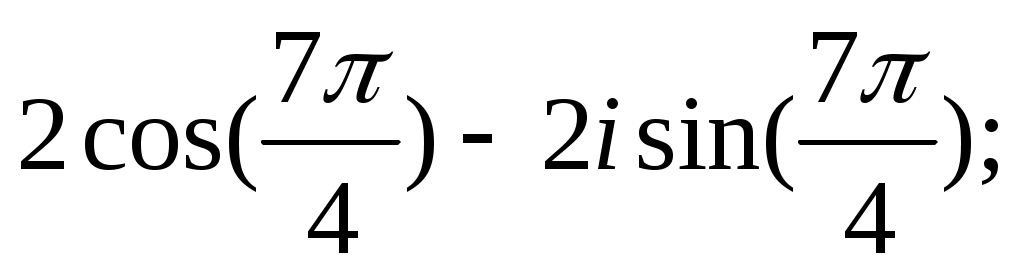
10)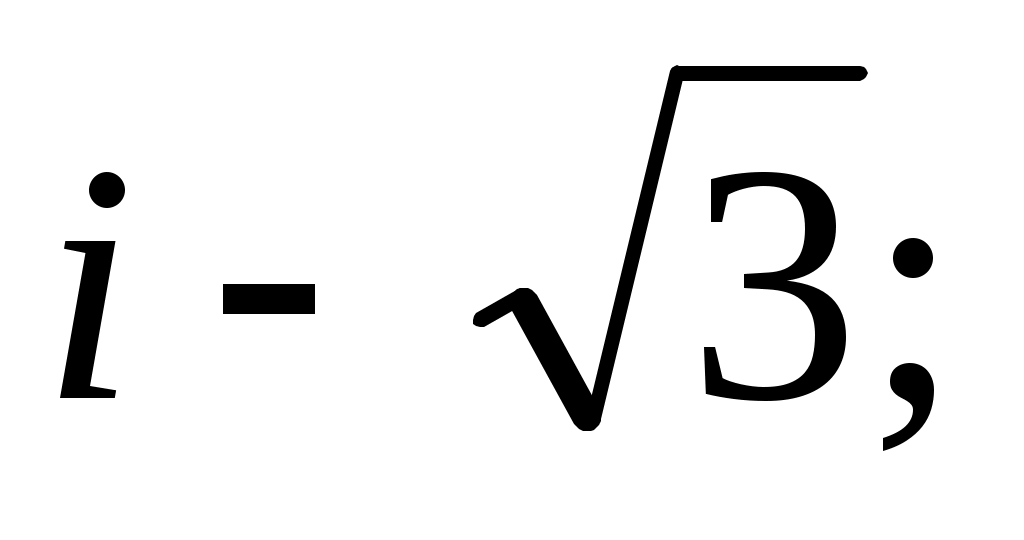
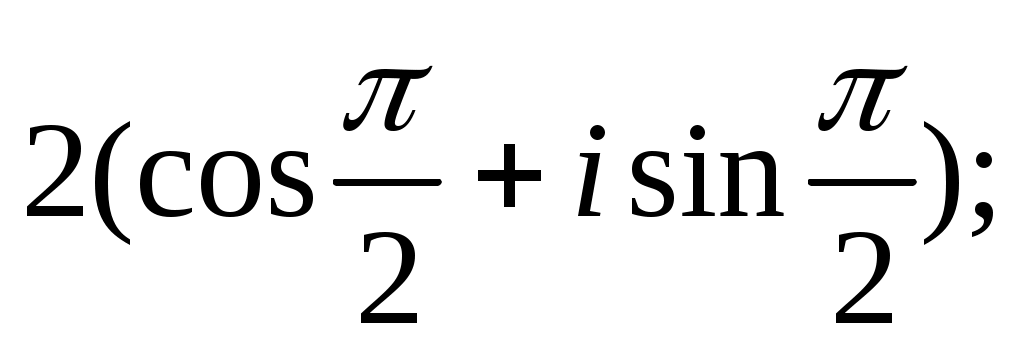
Задание V. Изобразить данное геометрическое место точек на комплексной плоскости.
1) |z + 1 - 3i| = 4, arg z = /2; 2) |z – 2 + 3i| < 5, arg z = -/3;
3) |z – 3i| < 1, arg z = 5/6; 4) |z + 2i| 7, arg z = -;
5) |z + 2i - 3| 3, arg z = 0; 6) |z + 3| + |z - 2i| 5;
7) |z + 3i| + |z - 1| < 3; 8) |z - (l + i)| + |z + (l + 2i)| 8;
9) |z + (l - i)| + |z - (2 + i)| 10; 10) |z + (1 – 2i)| + |z - 1| < 6;
Задание VI. Разложить многочлены, на множители, неприводимые над полями С, R и Q.
1. f(х) = х5 + х3 + x; 2. f(x) = х4 + х3 + 3х2 + 2х + 2;
3. f(х) = 27х4 - 9х2 + 14х - 4; 4. f(х) = х4 - х3 + 2х2 + х - 3;
5. f(х) = х4 - 2х3 - 3х2 + 4х + 4; 6. f(х) = х5 - х4 + 5х3 - 5х2 + 9х - 9;
7. f(х) = х6 + 27; 8. f(х) = х4 + 2х3 - х2 + 2х + 1;
9. f(х) = х4 - 4х3 + 8х2 - 16х + 16;
10. f(х) = х7 - х5 + х5 + х4 - х3 + x2 – 2x - 2.7 . ГЛОССАРИЙ
Группа — моноид (см. ниже), в котором каждый элемент имеет себе симметричный.
Группоид — непустое множество, замкнутое относительно одной бинарной операции.
Кольцо — алгебра с двумя заданными на ней бинарными операциями, являющаяся абелевой группой по сложению, в которой операция сложения связана с операцией умножения левым и правым дистрибутивными законами.
Комплексное число — пара действительных чисел.
Матрица — прямоугольная таблица, состоящая из k строк и s столбцов.
Многочлен — формальное выражение вида:.
Моноид — полугруппа (см. ниже) с нейтральным элементом.
Поле — кольцо, в котором каждый отличный от нуля элемент обратим.
Полугруппа — ассоциативный группоид.8. основная и дополнительная литература
8.1. Основная литература
Алгебра и теория чисел. / Под. ред. Н.Я. Виленкина. Изд.2-е. — М.: Просвещение, 2004. – 192 с.
Кострикин, А.И. Введение в алгебру. Основы алгебры. Учебник для вузов. – М.:Физматлит, 2003.- 320 с.
Куликов, Л.Я. Алгебра и теория чисел. М.: Высшая школа, 2005. – 559 с., ил
Куликов, Л.Я., Москаленко, А.И., Фомин, А.А. Сборник задач по алгебре и теории чисел. — М.: Просвещение, 2001. – 288 с..
Курош, А.Г. Курс высшей математики, — Изд.11-е. М.: Наука, 2006. – 432 с.
Фаддеев, Д.К., Соминский, И.С. Сборник задач по высшей алгебре, — М.: Наука. 2002. – 304 с.
Пуркина, В.Ф. Алгебра. Часть I. Горно-Алтайск, Универ-Принт, 2001. - 102 с.
Пуркина, В.Ф. Алгебра. Горно-Алтайск, 2006. - 240 с.
8.2. Дополнительная литература
Ван-дер Варден, Б. Л. Алгебра.- М.: Наука,1979. - 648 с., ил.
2. Калужнин, Л. А. Введение в общую алгебру. - М.: Наука, 1973.
Сборник задач по алгебре. Под. ред. А.И. Кострикина. — М.: Наука,1987, -352 с.
Кострикин, A. M. Основные структуры алгебры. - М.: 2001.
Скорняков, Л. А.Элементы алгебры. - М.: Наука, 1980.
Каргаполов, М. И., Мерзляков, Ю. И. Основы теории групп. - М.: Наука, 1977.
Мальцев, А. И. Алгебраические системы. - М.: Наука, 1970.
Воеводин, В. В.Линейная алгебра. - М.: Наука, 1980.
Ленг, С. Алгебра. - М.: Издательство Мир, 1968.
Белоногов, В. А.Задачник по теории групп. - М.: Наука, 1977.
Кострикин, А. И.Сборник задач по алгебре. - М.: 1995.
Воеводин, В. В., Кузнецов Ю. А. Матрицы и вычисления. – М.: Наука, 1984.
Гантмахер, Ф. Р. Теория матриц. – М.: Наука, 1966.
Икрамов, Х.Д. Задачник по линейной алгебре. – М.: Наука, 1975.
Ильин, В.А., Ким Г. Д. Линейная алгебра и аналитическая геометрия. – М.: МГУ, 1985.
Винберг, Э.Б. Алгебра многочленов. М.: Просвещение, 1980. – 176 с.
Варпаховский, Ф.Л., Солодовников, А.С. Алгебра. — Окунев, Л.Я. Высшая алгебра,— М.: Просвещение, 1966. – 333 с.
Для заметок
Для заметок
Для заметок
Учебное издание
Учебно-методический комплекс
«Алгебра»
Составители:
Пуркина Валентина Федоровна
Кайгородов Евгений Владимирович
Подписано в печать Формат 60*84/16
Бумага офсетная. Усл.печ.л.-
Заказ № . Тираж
РИО Горно-Алтайского госуниверситета,
649000, г. Горно-Алтайск, ул. Ленкина, д. 1
Отпечатано полиграфическим отделом
Горно-Алтайского госуниверситета,
649000, г. Горно-Алтайск, ул. Ленкина, д. 1
1 ... 8 9 10 11 12 13 14 15 16