Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc

§5. Методы нахождения корней многочлена

n - ой степени.

Итак, мы показали в п. 4, что достаточным условием приводимости многочлена над полями С, R, Q является наличие хотя бы одного корня многочлена f(x) в поле С, R или Q. Дня отыскания этих корней приходится решать уравнения n - ой степени в поле С, R или Q. Мы уже отмечали, что если многочлен f(x) имеет рациональный корень, то он приводим и над полем R, и над С. Поэтому, обычно, решение задачи о приводимости многочлена начинается с поиска его рациональных корней. Необходимые, но не достаточные условия существования рациональных корней многочлена с целыми коэффициентами даёт следующая теорема.

Теорема 1. Если - рациональный корень многочлена f(x) с целыми коэффициентами, причем (p, q) = l, то числитель дроби (р) является делителем свободного члена а₀, а знаменатель (q) является делителем старшего коэффициента а_n.

Доказательство.

Пусть - корень многочлена f(x)=a_nxⁿ + a_n-1x^n-1 +...+ a₁x + a₀, где все а_i Î Z. Подставим , где (p, q) = l, q ¹ 1 в многочлен, получим:

(1)

Умножим обе части равенства (1) на qⁿ, тогда:

a_npⁿ + a_n-1qp^n-1 +...+ a₁ pq^n-1 + a₀qⁿ = 0 (2)

Из равенства (2) сначала можно выразить

a_npⁿ = (-a_n-1p^n-1 -...- a₁pq^n-2 - a₀q^n-1)q => (а_n /q), а потом

-a₀qⁿ = p(a_np^n-1 + a_n-1p^n-2q+... …+ а₁q^n-l) => (а₀ /p) т.к. (p, q) = 1

Замечание 1. Так как   Z,   0 имеет лишь конечное число делителей, то теорема позволяет, путем конечного числа шагов, найти все рациональные числа многочлена или проверить что их нет.

Следствие 1. Нормированный многочлен f (x)  Z[x] не имеет дробных корней;

---

Следствие 2. Целый корень многочлена f(x)Z[x] является делителем свободного члена.

Задача 1. Разложить многочлен

f(x) = x⁶ - 2х⁵ + х⁴ + 6х³ - 10х² - 4х + 8

над полями Q, R и С.

Решение.

На основании теоремы (1), рациональные корни данного многочлена следует искать среди делителей числа 8, т.к. а_n = 1

Делители: + 1, ±2, ±4, ±8.

Известно, что число () является корнем многочлена f(x) тогда и только тогда, когда f(x) делится на (х - ) (Смотри п. 4). Следовательно, для проверки, какие из чисел ±1, ±2, ±4, ±8 являются рациональными корнями, можно использовать схему Горнера, а можно непосредственно проверить, будет ли f(±1) = 0, f(±2) = 0,

f(±4) = 0, f(±8) = 0.

	1	-2	1	6	-10	-4		8
1	1	-1	0	6	-4	-8		0
1	1	0	0	6	2	-6
-1	1	-2	2	4	-8	0
-1	1	-3	5	-1	-7  0
2	1	0	2	8	8  0
-2	1	-4	10	-16	24  0
4	1	2	10	44	166  0
-4	1	-6	26	…	 0
8	1	6	50	…	 0
-8	1	-10	42	…	- 0

---

Итак, f(x) = (x - l)(x + l)( x⁴ - 2x³ + 2x² + 4x - 8) над полем Q.

Чтобы найти разложение над полями R и С, нужно найти действительные и комплексные корни этого многочлена, для этого надо решить уравнение четвертой степени х⁴ - 2х³ + 2х² + 4х - 8 = 0.

Для решения уравнений 4-ой степени разработан частный метод Феррари.

1-й шаг. Оставляем в левой части равенства члены 4-ой и 3-ей степени, остальные переносим в правую часть, получим:

х⁴ - 2х³ = -2х² - 4х + 8

2-й шаг. Дополняем левую часть равенства до полного квадрата: х⁴ - 2х³ + х² = х² - 2х² - 4х + 8

(х² - х)² = -х² - 4х + 8

3-й шаг. Вводим новую переменную (у) и дополняем левую часть еще раз до полного квадрата, получим:

(х² - х)²+2(х²- x)у + у² = -х² - 4х + 8 + 2(х² - х)у + y²

[(x²-x)+y)]² = (2y-1)x²+(-2y-4)x+(y²+8) *

4-й шаг. Потребуем, чтобы правая часть также стала полным квадратом, для этого D = В² - 4АС = О

D=(-2y - 4)² - 4(2y - l)(y² + 8) = 0

у³ - у² + 6у – 6 = 0

Это уравнение имеет рациональный корень у₀ = 1.

5-й шаг. Подставим у₀ в правую и левую части уравнения (*) вместо у. Получим: (х²-х+1)² = х²-6х+9 = (х-3)² 

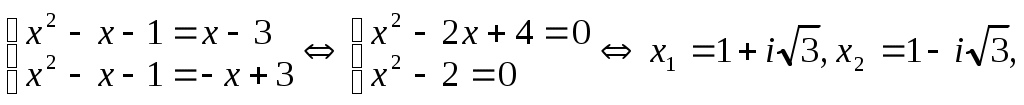x₃ = -2, x₄ = 2

Итак, многочлен f(x) над полем С может быть представлен в виде: f(х) = (х - 1)(х + 1)(х + 2)(х - 2)(x - 1- i3)(x - 1 + i3)

Для того, чтобы найти разложение многочлена над полем R, нужно перемножить две последние скобки, тогда:

f(х) = (х - 1)(х + 1)(х + 2)(x - 2)((х - 1)² + 3).

Задача 2. Разложить многочлен f(x) = х⁴ - 2х³ - 6х² - 4х - 1

Решение.

Так как многочлен 4-ой степени, то можно методом Феррари сразу искать его действительные и комплексные корни, а можно как и в первом случае, найти сначала рациональные корни (если они есть).

Так как а_n = 1, то многочлен может иметь в качестве рациональных корней целые числа, которые являются делителями свободного члена а₀ = 1, т.е. ±1. Непосредственной подстановкой убеждаемся, что (-1) является корнем, а (1) нет, т.к. f(-l) = 0, f(l) ¹ 0.

Тогда, f(x) = (х + 1)( х³ - 3х² - 3х - 1) над полем Q.

Теперь найдем корни многочлена в поле С и R.

Для этого решим уравнение:

х³ - 3х² - 3х - 1 = 0.

Это уравнение 3-ей степени, для таких уравнений также существует частный метод решения -

---

метод Кардано.

1- й шаг. Приведем уравнение к виду, не содержащему второй степени неизвестного. Для этого введем подстановку где (а) коэффициент при х² .

Тогда, (у + 1)³ - 3(у + 1)² - 3(у + 1) – 1 = 0. Раскрыв скобки и приведя подобные, получим: у³ - 6у - 6 = 0.

2-й шаг. Полагаем, что у =  + , где , р - коэффициент при у, q - свободный член.

В нашем случае р = -6, q = -6 Поэтому 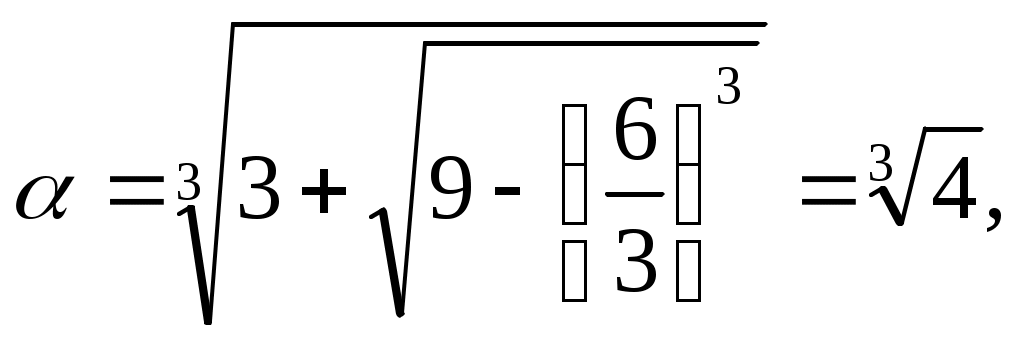тогда .

Тогда, ,



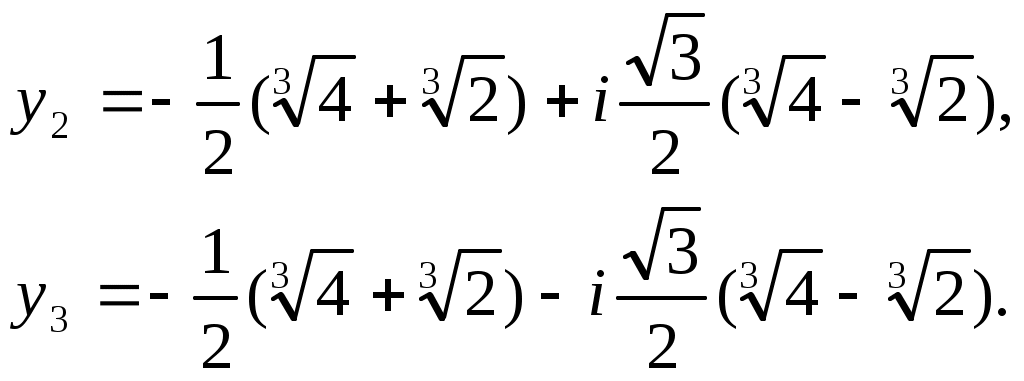
Наконец, находим (х) из формулы х = у + 1

,



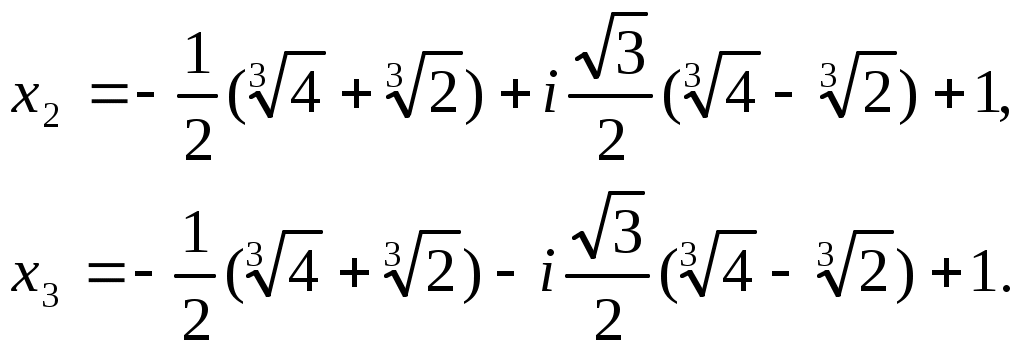
Тогда, f(x) = (x + l)(x – x₁)(x - x₂)(x - x₃) - разложение многочлена над полем С.

Для нахождения разложения многочлена f(x) над полем действительных чисел R достаточно в полученном выше разложении перемножить скобки, соответствующие сопряженным комплексным корням.

Тогда: над полем R.

Замечание 2. Если дан многочлен f(х), степень которого выше четвертой, причем он не имеет рациональных корней, то задача разложения многочлена f(x) на неприводимые многочлены над полем С и R становится трудноразрешимой, т.к. общих методов решения уравнений n-ой степени, где n > 4 не существует.

Существуют различные методы приближенного вычисления действительных корней многочлена f(x) (метод хорд, метод касательных и т.п.)

Замечание 3. В том случае, когда нужно найти сумму корней многочлена f(x), могут быть использованы формулы Виета, которые устанавливают зависимость между корнями и коэффициентами многочлена.

Выведем эти формулы:

---

Пусть f(z) = zⁿ + c₁z^n-1 + c₂z^n-2 +...+ c_n-1z + c_n и ₁, ₂,…, _n корни этого многочлена в поле С, тогда zⁿ + c₁z^n-1 + c₂z^n-2 +... + c_n-1z + c_n = (z - a₁)(z - a₂)...(z - a_n) = = zⁿ – (a₁ + a₂ +…+ a_n)z^n-1 + (a₁a₂ + a₁a₃ +…+ a_n-1a_n)z^n-2 +…+ +(-1)ⁿ (a₁a₂ …a_n)

Приравняв коэффициенты при соответствующих степенях, получим формулы Виета:

с₁ = -(a₁ + a₂ +…+ a_n)

с₂ = (a₁a₂ + a₁a₃ +…+ a_n-1a_n)

c₃ = -(a₁a₂a₃+ a₁a₂a₄ +…+ a_n-2a_n-1a_n)

с_n = (-1)ⁿ (a₁a₂ …a_n)

Задача 3. Найти сумму кубов корней многочлена

f(x) = x⁴ + 2х³ + х² + 5х + 3, f(x)Q[x]

Решение.

Над полем комплексных чисел С многочлен f(x) имеет четыре корня: х₁, х₂, х₃, х₄. Нам нужно найти X₁³+ X₂³+ X₃³+ X₄³ не находя самих корней.

По формулам Виета

х₁+x₂+ х₃+ х₄ = -2 =₁

х₁х₂ + х₁х₃ + х₁х₄ + x₂x₃+ х₂х₄ + х₃х₄ = 1 = ₂

х₁х₂х₃ + x₁x₂x₄ + х₁х₃х₄ + х₂х₃х₄ = -5 = s₃

х₁х₂х₃х₄ = 3 = s₄

Тогда X₁³+ X₂³+ X₃³+ X₄³ = ₁³ - 3₁₂ + 3₃ =

=(-2)³ - 3(-2)l + 3(-5) = -17

Ответ: -17.


6. ПРАКТИКУМ по АЛГЕБРЕ

---