Файл: Учебнометодический комплекс Для студентовбакалавров, обучающихся по направлению.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 187
Скачиваний: 3
СОДЕРЖАНИЕ
Глава 1. Понятия об основных алгебраических структурах.
§1. Алгебры. Подалгебры. Гомоморфизмы алгебр.
§3. Подгруппа. Достаточные условия подгруппы.
Глава 2. Матрицы и определители.
§1.Матрицы. Группа и кольцо матриц.
§2. Определители, их свойства.
Глава 3. Системы линейных уравнений, методы их решения.
Глава 5. Теория делимости в кольце Z.
§1. Отношение делимости в Z и его свойства.
§3. Взаимно простые числа и их свойства.
§4. НОК целых чисел и его свойства.
§5. Простые числа и их свойства.
Глава 6. Теория делимости в кольце Р[х].
§2. Отношение делимости в кольце Р[х] и его свойства.
Свойства отношения делимости в кольце Р[x].
§3. Деление с остатком в кольце P[x].
§4. Приводимые и неприводимые многочлены
Глава 5. Теория делимости в кольце Z.
Основные знания, умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:
-
знать определения отношений делимости без остатка и с остатком и их свойства; -
знать определения НОК, НОД, их связь, свойства и методы нахождения; -
знать алгоритм Евклида и уметь использовать его для нахождения НОД двух целых чисел; -
знать и уметь находить каноническое разложение натурального числа на простые множители.
§1. Отношение делимости в Z и его свойства.
Определение 1. Целое число (а) делится на целое число (b0), если q Z : a=bq
Обозначается: a/b и читается "а делится на b", или "b делит а".
а – делимое,
b – делитель,
q – частное.
Это отношение есть частичная бинарная операция на Z, т.к.
Свойства:
1. Отношение делимости рефлексивно. Действительно: a Z а/а, т.к. 1 Z : а = а 1
2. Отношение делимости транзитивно. Действительно:
" a, b, c Î Z (a/b & b/c) => (а/с), т.к. из того что (a/b)
q1 Z : a=bq1, а из того что (b/c) q2 Z : b=cq2, тогда
а = cq2q1 = cq3 => (а/с)
3. Отношение делимости антисимметрично, т.к. " a, b Î Z из того что (а/b & b/а) => [(а= b) v (a = -b)]
Следовательно, отношение делимости не является отношением эквивалентности, а будет отношением частичного порядка на множестве Z.
Определение 2. Целое число (а) делится на (bZ & b0) с остатком, если q, r Z : а = bq + r, где 0 < r < |b| а – делимое.
b – делитель, q - неполное частное, r — остаток.
Замечание 1. Из определения следует, что остаток всегда число неотрицательное.
Пример 1. Разделить - 49 на 17. Получим: - 49 = 17 • (-3)+2
Теорема 1. В кольце Z любое целое число (а) можно разделить на целое число (b0) с остатком, единственным образом.
1. Покажем возможность деления.
Пусть bq - наибольшее кратное числа b, которое не превосходит (а), тогда bq а b(q+l) => 0 a-bq b положим, что a-bq = г, тогда получим, что а = bq + r, где 0< r <|b|.
2. Докажем единственность такого представления. Предположим противное,
Пусть a=bq1+r1, 0
=> b(q1 -q2) = (r1-r2) => (r2-r1)/b , а т.к. |r2-r1|<|b| =>
=> (r2-r1) = 0 => (r2 = r1)
Т.к. b¹0 то из равенства b(q1-q2) = 0 => (q1-q2) = 0 => (q1 = q2).
§2.НОД(а, b), HOK(a, b). Алгоритм Евклида.
Определение 1. Целое число dZ, (d¹0) называется общим делителем чисел a1,а2,..ak,если каждое ai(i=1,2,..., к) делится на d.
Определение 2. Целое число dZ, (d¹0) называется наибольшим общим делителем чисел a1,а2,... ,ак если:
1 d - общий делитель всех аi
2. d - делится на любой другой общий делитель этих чисел
Обозначение: НО Д (a1 ,а2,. . ak)= d или (а1 ,а2,…,ak) = d
Пример 1. Даны числа: 4, 8, 12, 16, 20, 24, 48
Числа 2 и 4 являются общими делителями этих чисел Число 4 является наибольшим общим делителем данных чисел, т е НОД (4, 8, 12, 16, 20, 24, 48) = 4
Задача 1. Доказать, что d = (a, b) определяется однозначно с точностью до знака.
Доказательство.
Пусть d1 = (a, b) & d2 = (a, b) => (d1 / d2)&(d2 / d1) => [(d1 = d2) v (d1 = -d2)].
Замечание 1. Обычно берется положительное значение d = (a,b).
Существует метод, который позволяет доказать существование НОД (а, b) и находить его для любой пары целых чисел, его называют алгоритмом Евклида. Он основан на двух леммах:
Лемма 1. Если (а /b), то (a,b)=b.
Лемма 2. Если а = bq + г, где а, b, r 0, то (а, b) = (b, r).
Алгоритм Евклида.
1 Шаг. Делим а на (b¹0), если а /b, то (a, b) = b по лемме 1, если а = bq0 + r1, то (a, b)=(b, r1)
2Шаг. Делим b на r1 если (b /r1) => (b, r1) = r1, если b = r1q1+r2, то (b, r1) = (r1, r2).
3 Шаг. Делим r1 на r2и т. д.
Поскольку остатки, получаемые в процессе деления, убывают и являются натуральными числами, то на каком-то шаге получим остаток, равный нулю, т.е. rn-1 = rnqn и тогда (rn-1, rn) = rn.
Задача 2. Доказать, что последний неравный нулю остаток в алгоритме Евклида является наибольшим общим делителем чисел (а) и (b).
Решение: Применим к числам (а) и (b) алгоритм Евклида:
a = bqo+r1 0r1
b = r1q1 + r2 0 r2
. . . . . . . . . . . . . . . . . . . . .
rn-2=rn-1•qn-1 +rn 0
rn-1 =rnqn + 0
Из первого равенства по лемме 2 будем иметь:
(a, b) = (b, r1)
Из второго равенства алгоритма Евклида тоже по лемме 2 будем иметь (b, r1)= (r1 г2) и т. д.
Из последнего равенства (rn-1 , rn) = rn по лемме 1. Т.е. получили цепочку равенств (а, b) = (b, r1) = (r1, r2) = (r2, r3) = …..
=(rn-2, rn-1) = (rn-1, rn) = rn
Итак, (а, b)=rn.
Пример 2. Найти d = (3220,1550) с помощью алгоритма Евклида
Решение:
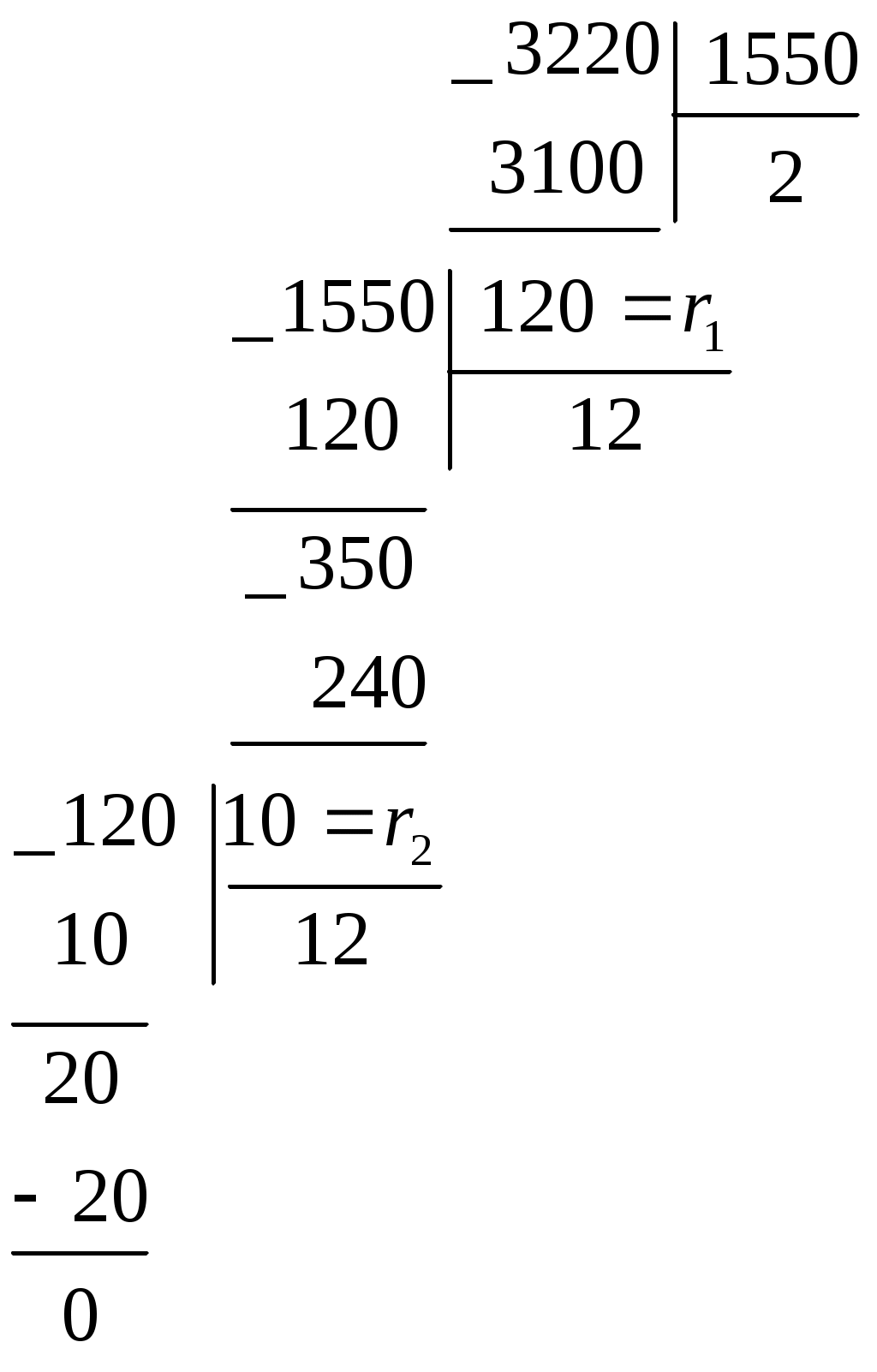
Итак, (3220, 1550) = 10 = r2
Задача 3. Доказать, что если d=(а,b), то х, у
d = ах + by.
Решение:
Применим к числам а и b алгоритм Евклида:
а = bq0 + r1
b = r1 q1 + r2
ri = r2q2 + r3
……………………
rn-3 = rn-2qn-2 + rn-1
rn-2 = rn-1qn + d, (d = rn)
Тогда, последовательно выражая, из последнего равенства, d = rn-2 - rn-1 qn (*) из предпоследнего rn-1 = rn-3 – rn-2qn-2 и т.д.
Из первого r1 = а-bqo и последовательно подставляя их в равенство (*) получаем: d = ах + by.
§3. Взаимно простые числа и их свойства.
Определение1. Целые числа а1 ,а2,…,akназываются взаимно-простыми, если (а1 ,а2,…,ak )=1
Определение 2. Целые числа а1 ,а2,…,ak называются попарно взаимно-простыми, если i,s (i, s = 1, 2, .. , к, is, (аi, аs) =1).
Если числа удовлетворяют определению 2,то они удовлетворяют и определению 1. Обратное утверждение в общем случае неверно, например: (15, 21, 19)= 1, но (15, 21) = 3
Теорема (критерий взаимной простоты)
(а, b) = 1 <=> х, у Z: ах + by = 1
Доказательство:
Докажем необходимость. Пусть (а, b) = 1. Выше мы показали, что если d=(a,b), то х, y Z : d = ax +by.
Т.к. в этом случае d =1, то будут х, y Z (определяемые из алгоритма Евклида): 1 = ах + bу.
Достаточность. Пусть (*) ах + by = 1, докажем, что (а, b)=1. Предположим, что (a, b) = d, тогда в левой части равенства (*)
(a /d) & (b /d) => (ах + by) /d => (1/d) => (d=l) => (a, b) = 1.
§4. НОК целых чисел и его свойства.
Определение 1. Общим кратным конечного множества целых чисел а1 ,а2,…,ak, отличных от нуля, называют целое число m, которое делится на все числа ai (i=l, 2,…, к)
Определение 2. Целое число (m) называется наименьшим общим кратным чисел а1 ,а2,…,ak, отличных от нуля, если:
1 m - является их общим кратным;
2 (m) делит любое другое общее кратное этих чисел.
Обозначение: m = НОК (а1 ,а2,…,ak) или m = [а1 ,а2,…,ak]
Пример. Даны числа: 2, 3, 4, 6, 12.
Числа 12, 24. 48. 96 являются общими кратными чисел 2, 3, 4, 6, 12 Наименьшим общим кратным будет число 12. т.е.
[2, 3, 4, 6, 12] = 12
НОК определяется однозначно с точностью до порядка следования сомножителей. Действительно, если предположить, что m1= [а, b] &m2 = [a, b] (m1 / m2) & (m2/m1) => [(m1 = m2) v (m1= - m2)]. Между наименьшим общим кратным и наибольшим общим делителем двух целых чисел существует зависимость, которая выражается формулой: [а, b] = ab/(а, b) (выведите ее самостоятельно)
Эта связь позволяет утверждать, что для любой пары целых чисел, отличных от нуля, существует их наименьшее общее кратное. Действительно, (а, b) – всегда можно однозначно вывести из алгоритма Евклида и по определению (а, b) 0, тогда дробь ab/(а, b) 0 и будет определена однозначно.
Наиболее просто НОК двух целых чисел вычисляется в том случае, когда (а,b)= 1, тогда [а, b] = ab/1 = а • b
Например, [21, 5] = 215/1 = 105, т. к. (21, 5) = 1.
§5. Простые числа и их свойства.
Определение 1. Натуральное число (р) называется простым, если р > 1 и не имеет положит. делителей, отличных от 1 и р.
Определение 2. Натуральное число а >1, имеющее кроме 1 и самого себя другие положительные делители, называется составным.
Из этих определений следует, что множество натуральных чисел можно разбить на три класса:
а) составные числа;
б) простые числа;
в) единица.
Если а - составное, то а = nq, где 1
Задача 1. Доказать, что если aZ и р - простое число, то (а, р) = 1 v (a / р)
Доказательство.
Пусть d = (а, р) => (a /d) & (р /d), т.к. р - простое число, то оно имеет два делителя 1 и р. Если (а, р) = 1, то а и р взаимно просты, если (а, р) = р, то (а/р).
Задача 2. Если произведение нескольких сомножителей делится на р, то по крайней мере один из сомножителей делится на р.
Решение.
Пусть произведение (а1,а2,...,аk)/р, если все ai не будут делиться на р, тогда и произведение будет взаимно просто с р, следовательно, какой-то сомножитель делится на р.
Задача 3. Доказать, что наименьший отличный от 1 делитель целого числа а>1, есть число простое.
Доказательство.
Пусть aZ и а - составное число (если а = р, то утверждение доказано), тогда а = a1q.
Пусть q - наименьший делитель, покажем, что он будет простым числом. Если предположить, что q - составное число, тогда q = q1k и а = a1•q1k, т.к. q1
Задача 4. Доказать, что наименьший простой делитель (р) натурального числа (n) не превосходит n .
Доказательство.
Пусть n = рn1, причем р < n1 и р - простое. Тогда n р2 => р<n .
Из этого утверждения следует, что если натуральное число (n) не делится ни на одно простое число р n , то n – простое, в противном случае оно будет составным.
Пример 1. Выяснить, будет ли число 137 простым? 11 <137 <12.
Выписываем простые делители, не превосходящие 137: 2, 3, 5, 7, 11. Проверяем, что 137 не делится на 2, на 3, на 5, на 7, на 11. Следовательно, число 137 – простое.
Теорема Евклида. Множество простых чисел бесконечно.
Доказательство.
Предположим противное, пусть p1,p2,...,pk все простые числа, где p1 = 2, а pk – самое большое простое число.
Составим натуральное число = p1p2 ...pк +1, т.к. pi , то оно должно быть составным, тогда его наименьший делитель будет простым (см. задачу 3). Однако не делится ни на p1 , ни на p2 ,…, ни на pk , т.к. 1 не делится на любое pI.
Следовательно, наше предположение о конечности множества простых чисел было неверно.
Однако существует теорема, которая утверждает, что простые числа составляют лишь небольшую часть чисел натурального ряда.
Теорема об интервалах. В натуральном ряду существует сколь угодно длинные интервалы, не содержащие ни одного простого числа.
Доказательство.
Возьмём произвольное натуральное число (n) и составим последовательность натуральных чисел (n+1)!+2, n+1)!+3,…,(n+1)!+(n+1).
В этой последовательности каждое последующее число на 1 больше предыдущего, все эти числа составные, т.к. каждое имеет более двух делителей (например, первое число делится на 1, на 2 и само на себя). При n→∞ мы получим сколь угодно длинный интервал, состоящий только из составных чисел.
Теорема Евклида и теорема об интервалах свидетельствуют о сложном характере распределения простых чисел в натуральном ряду.
Основная теорема арифметики
Любое натуральное число n>1 может быть представлено единственным образом в виде произведения простых чисел, с точностью до порядка следования сомножителей.
Доказательство.
Докажем возможность представления:
Пусть nN и n>1, если n – простое число, то n = p и теорема доказана. Если n – составное, то наименьший его делитель будет числом простым и n = p1n1, где n1
Далее рассуждаем аналогично. Если n1 простое число, то теорема доказана, если n1