Файл: Задания по теме 1 Методика изучения основных величин в начальной школе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 988
Скачиваний: 39
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 8. Изучите конспект урока.
Урок математики в 4 классе по теме «Доли и дроби».
Цель урока: дать общее представление о долях, научить учащихся называть, записывать и сравнивать доли
Задачи урока:
- обучающие – ввести новое понятие «доля числа», учить определять долю числа, записывать дроби, познакомить с терминами «доля», «дробь», «числитель», «знаменатель»;
- развивающие – развивать логическое мышление, математическую речь, навыки устного счета, внимание, память, мышление;
- воспитывающие – воспитывать коллективизм, аккуратность.
Ход урока
1. Знакомство с темой урока.
– Людям часто приходится делить целое на доли. А помните известный мультик «Апельсин» Посмотрим, как животные делили апельсин. Смотрите внимательно, после просмотра я задам вам вопросы.
- Как в песенке, животные называют равные части? (Дольки).
– Кто из вас был внимательным? Сколько долек было в апельсине? (Пять долек).
– Сколько долек поучил каждый? (Одну дольку апельсина).
- Как вы думаете, апельсин был разделён на равные части? (Да).
- Как по-другому, можно назвать эти равные части? (Доли).
2. Постановка учебных задач.
- Как на языке математики назвать и записать, какую долю (часть) апельсина получил каждый из животных? ( Не знаем)
- Что, на ваш взгляд, нам следует узнать, чему научиться? (Научиться записывать, называть и сравнивать доли).
- В результате совместных рассуждений, мы определили цель урока. (Научиться записывать, называть и сравнивать доли).
3. Работа над формированием понятий «Доли» и «Дроби».
- Давайте, определим, что же называют долями? Для этого еще раз вспомним, как животные делили апельсин
- Сколько частей досталось каждому животному? ( По одной части).
- Что можно сказать про каждую из частей? Какие это части? (Равные).
- Значит, каждому досталось по одной равной части от целого апельсина.
- Сделайте вывод, что такое доля. (Доля – это одна или несколько равных частей целого.)
(На доске появляется запись: 1 часть из 5).
В математике пишут короче: 1/5. Для записи понадобится 2 клеточки, между ними проводим черту. Число под чертой показывает, на сколько равных частей мы разделили предмет, а над чертой – сколько таких частей взяли. Читаем запись, запишите.
- Когда мы «делим» натуральные числа, то используем знак (:).
- Но в математике есть еще один знак деления, он называется, «дробная черта» - соответственно числа, записанные с этим знаком, называются дробными.
- Кто догадался, как называется данная запись? (Дробь).
- Верхняя часть дроби называется числителем, а нижняя – знаменателем.
- Что обозначает знаменатель в записи дроби? (На сколько частей разделили предмет).
- Что обозначает числитель? (Сколько частей взяли).
4. Отработка умения находить часть от целого и обозначать её дробью. Сравнение дробей.
Вопросы:
¾ Разработайте задания для 4 этапа урока (работа с количеством заданий – не менее 6 заданий).
1 задание
В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
2 задание
Было 600 рублей,
3 задание
Какую часть от числа 20 составляет 5?
-
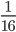 2)
2) 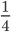 3)
3) 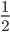 4) 2
4) 2
4 задание
Сравните:
-
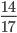 и
и 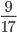 2)
2) 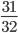 и 1 3)
и 1 3) 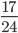 и
и 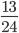 4)
4) 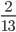 и
и 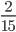
¾ Какие вопросы можно предложить учащимся на этапе рефлексии?
-
Над формированием, каких умений работали на уроке? -
«Цветные карточки».
У учащихся две карточки: синяя и красная. Они показывают карточку в соответствии с их настроением в начале и в конце урока. В данном случае мы можем проследить, как меняется эмоциональное состояние ученика в процессе занятия.
-
Что открыли, узнали на уроке? -
Над чем заставил задуматься урок? -
Что открыли, узнали на уроке? -
Что было выполнить легко, а что оказалось неожиданно трудно? -
Выберите 1 фразу для соседа по парте:
Ты молодец.
Я доволен твоей работой на уроке.
Ты мог бы поработать лучше.
Задания по теме 5.5 Обучение элементам алгебры в начальной школе
Цель: формирование умений проектировать учебную деятельность с учетом возраста и индивидуальных особенностей обучающихся; умений находить и использовать методическую литературу и другие источник информации, необходимые для подготовки к урокам.
Задание 9.Разработайте дифференцированные задания для самостоятельной работы (высокого, среднего, низкого уровня сложности) для учащихся начальной школы по проверке умений и навыков решать уравнения различного вида (не менее 5 заданий по 3 уровня сложности в каждом задании).
| № задания | Высокий уровень | Средний уровень | Низкий уровень |
| 1 | Докажи, не выполняя вычислений, что значения выражений в каждом столбике одинаковы. 9х7+9+5= 8х6+8+3= 7Х9+9+5= 8Х7+3= 9Х8+5= 7Х8+3= | Найди значение, используя данные равенства: 5Х9=45 6Х9=54 7Х9=63 45:5= 54:6= 63:7= 45:9= 54:9= 63:9= | Найди значение, используя данные равенства: 24-8-8-8=0-----24:8=* 10-2-2-2-2-2=0-----10:2=* 24-6-6-6-6=0—24:6=* 10-5-5=0-------------10:5=* |
| 2 | Измените вопрос и условие задачи (см. задание для 2-й группы) так, чтобы общее количество конфет стало лишним данным. Запишите новую задачу и решите ее. | Решите задачу: «Для новогодних подарков привезли 48 кг конфет. В пакетах было 12 кг конфет, в коробках в 3 раза меньше, чем в пакетах, а остальные конфеты были в ящиках. Сколько конфет было в ящиках?» | Решите задачу: «Для новогодних подарков привезли 48 кг конфет. В пакетах было 12 кг конфет, в коробках в 3 раза меньше, чем в пакетах, а остальные конфеты были в ящиках. Сколько конфет было в ящиках?» |
| 3 | Составь уравнения, используя следующие выражения: 43-3, 20+5, 12+7. | Составьте и решите задачу на тему: Уравнение. | Посмотри на уравнения, найди в них ошибки и исправь их. 1. Х-8=12 Х=12-8 Х=20 2. Х+3=10 Х=10-3 Х=5 3. 10-Х=7 Х=10+7 Х=3 |
| 4 | Поезд прошел без остановок 420 км со скоростью 70 км/ч, после остановки на 14 минут прошел еще 300 км со скоростью 75 км/ч. Какое расстояние он преодолел? Какое расстояние прошел поезд обратно? | Поезд прошел без остановок 420 км со скоростью 70 км/ч, после остановки на 14 минут прошел еще 300 км со скоростью 75 км/ч. Какое расстояние он преодолел? Запиши решение задачи выражением. | Поезд прошел без остановок 420 км со скоростью 70 км/ч, после остановки на 14 минут прошел еще 300 км со скоростью 75 км/ч. Какое расстояние он преодолел? Реши задачу по действиям. Какая величина в условии лишняя? |
Задание 10. Составьте систему упражнений для формирования понятия «выражение» и изучения порядка действий в числовых выражениях (не менее 6 упражнений).
Задание № 1
Из заданных пар примеров выпишите только те, в которых вычисления выполнены по правилам порядка действий.
20+30:5=10
20+30:5=25
42-12:6=40
42-12:6=5
Задание № 2
Расставь скобки, чтобы получились верные равенства.
60-20+30:5=50
60-20-30:5=46
60-20+30:5=14
Задание № 3
Вычисли значение данного выражения, предварительно указав порядок действий.
68 + 36 + 2 * 5 =
Задание № 4
Сколько дней в трёх неделях?
Задание № 5
Сколько сдачи получит Маша со 100 рублей, если истратит 72 рубля?
Задание № 6
Сколько понадобится парт, чтобы рассадить парами 26 учеников?