Добавлен: 26.10.2023
Просмотров: 561
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
которые в дальнейшем постепенно затвердевают, то твердые частицы могут иметь форму микрокристаллов, так и микроскопических шариков. Что касается частиц дисперсионных аэрозолей, и прежде всего пыли, то они всегда имеют неправильную форму.
По форме частицы делятся на три группы:
Частицы-агрегаты возникают в результате коагуляции первичных частиц, причем такой агрегат может быть образован в некоторых случаях всего двумя первичными частицами, в других – несколькими миллионами частиц.
По форме различают два типа агрегатов: изометрические и линейные (или цепные). Линейные агрегаты представляют собой цепочки, образованные первичными частицами и имеющими иногда многочисленные разветвления. Возникновение агрегата определенного типа зависит от природы и состава аэрозольных частиц, от состава газовой среды, в значительной степени от наличия электрического поля и т.д.
Для характеристики аэрозольных частиц совершенно неправильной формы вводят специальное понятие – «степень неправильности», или так называемый формфактор. За степень неправильности обычно понимают отклонение формы частицы от шарообразной. В настоящее время наиболее часто используется понятие эквивалентной частицы, которая по каким-либо параметрам подобна действительной частице.
Изучение движения частиц аэрозоля, их осаждения и коагуляции составляют предмет весьма важного раздела учения об аэродисперсных системах, который можно назвать механикой аэрозолей. Сюда же целесообразно отнести тесно примыкающий к проблемам осаждения и коагуляции вопрос о явлениях, происходящих при соприкосновении частиц друг с другом и с макроскопическими телами, а также мало изученный вопрос об обратных процессах – отрыве частиц от стенок и переходе порошкообразных тел в аэрозольное состояние.
Таким образом, предметом механики аэрозолейявляется изучение явлений и процессов с аэрозолями после стадии их образования. Здесь наблюдается полная аналогия с пониманием механики как одного из разделов физики. Задачи механики аэрозолей – разработка адекватных физико-математических моделей процессов и явлений эволюции аэрозолей и создание эффективных экспериментальных методик их исследования, которые не только верифицируют теоретические предсказания, но и открывают новые стороны явлений и процессов. Основные направления, где необходимы результаты решения данных задач – процессы в аэрозольных технологиях, газоочистка, механика атмосферного аэрозоля.
Частицы пыли, дыма или тумана при свободном падении быстро достигают такой постоянной скорости, при которой аэродинамическое сопротивление, действующее на частицу, становится равным ее весу. Если размер частицы сравним с средней длиной свободного пробега молекул газа, то удары этих молекул приводят к случайному (броуновскому) движению, которое накладывается на ее гравитационное оседание. При очень малых размерах частицы и коротком времени наблюдения падение ее полностью маскируется броуновским движением. При рассмотрении скорости падения целесообразно взять простейший случай оседания жесткой сферической частицы в газе в отсутствие влияния других частиц и стенок сосуда. Если частица велика по сравнению с длиной свободного пробега газовых молекул, но не настолько велика, чтобы могли проявиться эффекты, связанные с инерцией газообразной среды, то применим закон Стокса. Приравнивая сопротивление Стокса эффективному весу шара, имеем:
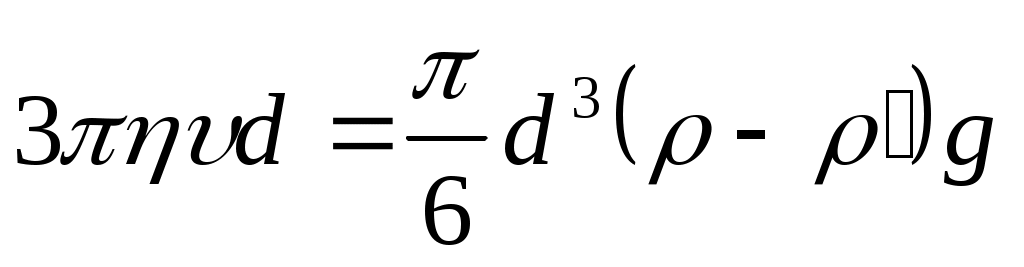
(4.1)
где d — диаметр шара; υ — его конечная скорость падения; ρ — его плотность; η— вязкость воздуха, ρ' — его плотность; g — ускорение силы тяжести. Таким образом, если пренебречь ρ' по сравнению с ρ:
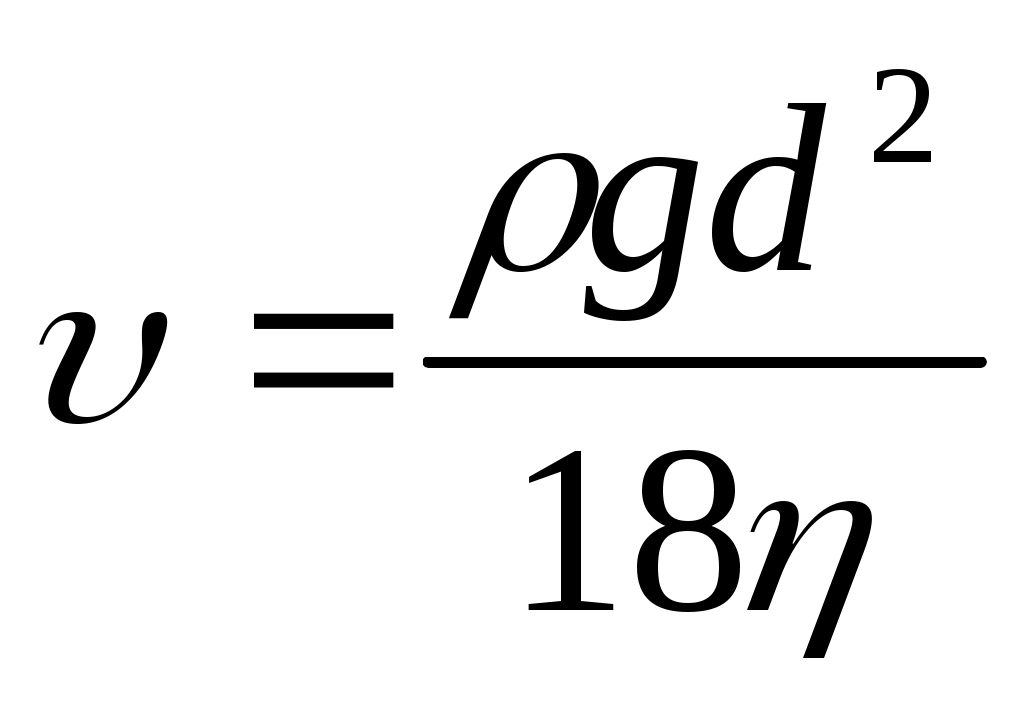 (4.2)
(4.2)
Закон Стокса справедлив, если можно пренебречь влиянием инерции воздуха, вытесненного шаром, или другими словами, если отношение сил инерции к силам вязкости, т. е. число Рейнольдса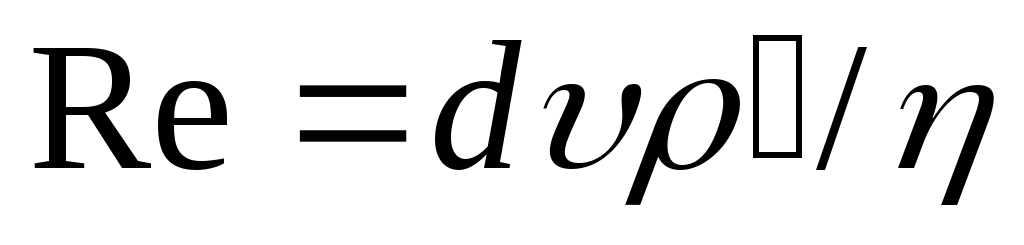 очень мало. В результате многочисленных экспериментов с шарами в различных средах было найдено, что при Re<0,05 отклонение от закона Стокса не превышает 1%; Re=0,05 соответствует падению шара с плотностью 1 и диаметром 29 мк в воздухе. При более высоких Re отклонения возрастают и закон Стокса начинает давать завышенную скорость оседания.
очень мало. В результате многочисленных экспериментов с шарами в различных средах было найдено, что при Re<0,05 отклонение от закона Стокса не превышает 1%; Re=0,05 соответствует падению шара с плотностью 1 и диаметром 29 мк в воздухе. При более высоких Re отклонения возрастают и закон Стокса начинает давать завышенную скорость оседания.
Таблица 2 - Поправочные коэффициенты для расширения применимости закона Стокса
Частицы могут выводиться из аэрозольной системы двумя путями: 1) они способны коагулировать (агрегировать) с другими частицами и укрупняться до таких размеров, что будут интенсивно оседать на поверхности под действием силы тяжести; 2) могут мигрировать к поверхностям осаждения, ударяться о них и оставаться связанными с ними. Процессы, вследствие которых аэрозольные частицы перемещаются к поверхности либо друг к другу без действия на них внешних сил, называются диффузионными, а движение частиц в таких процессах – броуновским движением.
Также часто употребляется термин броуновская диффузия аэрозолей, он подразумевает перенос частиц из областей с большей их концентрацией в области с меньшей концентрацией.
Аэрозольные частицы, взвешенные в газе, беспорядочно перемещаются из-за соударений с молекулами газа. Можно сказать, что броуновское движение аэрозолей «проявляет» скрытое тепловое молекулярное движение. Это явление в 1828 году впервые наблюдал в жидкостях шотландский ботаник Броун, в честь которого оно и получило свое наименование. В 1881 году Бодашевский изучил броуновское движение аэрозолей и нашел, что оно подобно хаотическому движению молекул газа, постулируемому кинетической теорией.
Законы, описывающие броуновскую диффузию частиц
Аэрозольные частицы можно представить себе как один из компонентов многокомпонентной газовой смеси, тогда возможны и справедливы известные физические и математические аналогии с процессами диффузии в газах. Когда аэрозольные частицы однородно распределены в газе, броуновское движение будет изменять расположение отдельных частиц, но не ансамбля частиц как целого. Если же наблюдаются какие-либо неоднородности распределения частиц в пространстве, то броуновское движение будет способствовать выравниванию концентраций частиц в газе: из областей с высокими концентрациями они будут перемещаться в области с низкими концентрациями. Этот процесс диффузии частиц описывается теми же феноменологическими законами, что и процессы молекулярной диффузии – законами Фика.
Согласно первому закону Фика:
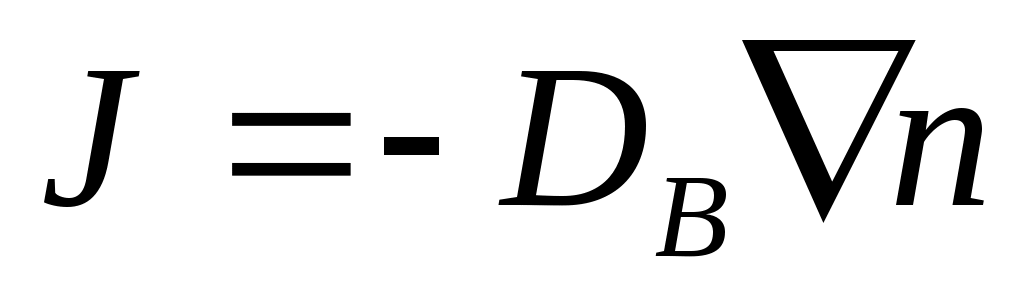 (4.3)
(4.3)
где J – плотность потока частиц (1/(м²·с)), n – числовая концентрация (1/м³),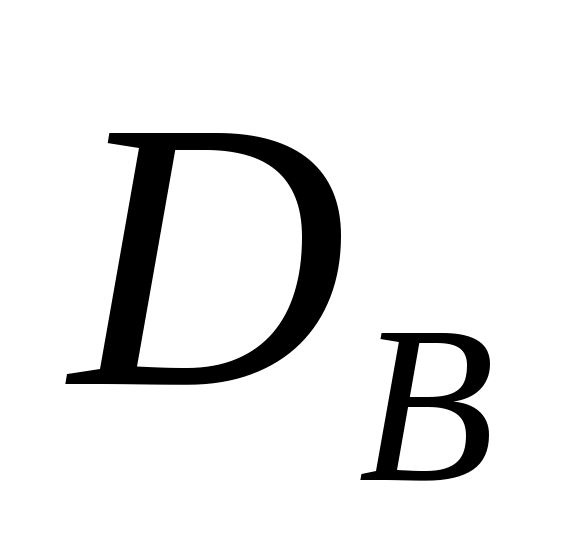
(м²/с) – коэффициент броуновской диффузии частиц. Этот закон описывает процесс стационарной диффузии и формулируется следующим образом: плотность потока аэрозольных частиц через поверхность, нормальную к направлению переноса, пропорциональна градиенту концентрации частиц, взятому с обратным знаком.
Согласно второму закону Фика:
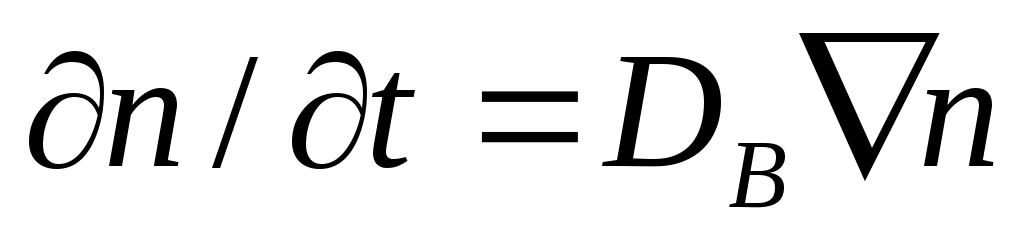 . (4.4)
. (4.4)
Он описывает процесс нестационарной диффузии частиц в пространстве и формулируется так: производная концентрации аэрозольных частиц по времени в данной точке пространства пропорциональна лапласиану концентрации в этой точке.
Законы Фика являются феноменологическими и не могут расшифровать структуру коэффициента броуновской диффузии , для этого требуется разработка микроскопической модели процесса броуновской диффузии. Если же эта задача будет решена, то уравнения (4.3) и (4.4) с соответствующими начальными и граничными условиями в принципе позволяют решать любые задачи диффузии аэрозолей в пространстве.
, для этого требуется разработка микроскопической модели процесса броуновской диффузии. Если же эта задача будет решена, то уравнения (4.3) и (4.4) с соответствующими начальными и граничными условиями в принципе позволяют решать любые задачи диффузии аэрозолей в пространстве.
Теория броуновского движения Эйнштейна
В 1905-1906 гг. А. Эйнштейн опубликовал результаты, которые сегодня считаются основополагающими и классическими в теории броуновского движения аэрозольных частиц. В частности, им были получены выражения для среднего квадрата смещения частицы при ее броуновском движении и коэффициента броуновской диффузии частиц .
.
Таблица 3 - Окончательные результаты теории Эйнштейна
По форме частицы делятся на три группы:
-
Изометрические частицы, у которых все три размера имеют примерно одинаковую величину, причем по форме такие частицы близки к шару и правильным многогранникам. Поэтому аэрозоли с изометрическими частицами называются иногда изометрическими, в отличии от анизометрических, частицы которых имеют неправильную форму; -
Ламинарные частицы, у которых два размера преобладают над третьим; -
Фибропластинчатые частицы, которые имеют форму волокон, то есть те, у которых преобладает один из трех размеров.
Частицы-агрегаты возникают в результате коагуляции первичных частиц, причем такой агрегат может быть образован в некоторых случаях всего двумя первичными частицами, в других – несколькими миллионами частиц.
По форме различают два типа агрегатов: изометрические и линейные (или цепные). Линейные агрегаты представляют собой цепочки, образованные первичными частицами и имеющими иногда многочисленные разветвления. Возникновение агрегата определенного типа зависит от природы и состава аэрозольных частиц, от состава газовой среды, в значительной степени от наличия электрического поля и т.д.
Для характеристики аэрозольных частиц совершенно неправильной формы вводят специальное понятие – «степень неправильности», или так называемый формфактор. За степень неправильности обычно понимают отклонение формы частицы от шарообразной. В настоящее время наиболее часто используется понятие эквивалентной частицы, которая по каким-либо параметрам подобна действительной частице.
4 Элементы механики аэрозолей
Изучение движения частиц аэрозоля, их осаждения и коагуляции составляют предмет весьма важного раздела учения об аэродисперсных системах, который можно назвать механикой аэрозолей. Сюда же целесообразно отнести тесно примыкающий к проблемам осаждения и коагуляции вопрос о явлениях, происходящих при соприкосновении частиц друг с другом и с макроскопическими телами, а также мало изученный вопрос об обратных процессах – отрыве частиц от стенок и переходе порошкообразных тел в аэрозольное состояние.
Таким образом, предметом механики аэрозолейявляется изучение явлений и процессов с аэрозолями после стадии их образования. Здесь наблюдается полная аналогия с пониманием механики как одного из разделов физики. Задачи механики аэрозолей – разработка адекватных физико-математических моделей процессов и явлений эволюции аэрозолей и создание эффективных экспериментальных методик их исследования, которые не только верифицируют теоретические предсказания, но и открывают новые стороны явлений и процессов. Основные направления, где необходимы результаты решения данных задач – процессы в аэрозольных технологиях, газоочистка, механика атмосферного аэрозоля.
4.1 Скорость падения частиц
Частицы пыли, дыма или тумана при свободном падении быстро достигают такой постоянной скорости, при которой аэродинамическое сопротивление, действующее на частицу, становится равным ее весу. Если размер частицы сравним с средней длиной свободного пробега молекул газа, то удары этих молекул приводят к случайному (броуновскому) движению, которое накладывается на ее гравитационное оседание. При очень малых размерах частицы и коротком времени наблюдения падение ее полностью маскируется броуновским движением. При рассмотрении скорости падения целесообразно взять простейший случай оседания жесткой сферической частицы в газе в отсутствие влияния других частиц и стенок сосуда. Если частица велика по сравнению с длиной свободного пробега газовых молекул, но не настолько велика, чтобы могли проявиться эффекты, связанные с инерцией газообразной среды, то применим закон Стокса. Приравнивая сопротивление Стокса эффективному весу шара, имеем:
(4.1)
где d — диаметр шара; υ — его конечная скорость падения; ρ — его плотность; η— вязкость воздуха, ρ' — его плотность; g — ускорение силы тяжести. Таким образом, если пренебречь ρ' по сравнению с ρ:
Закон Стокса справедлив, если можно пренебречь влиянием инерции воздуха, вытесненного шаром, или другими словами, если отношение сил инерции к силам вязкости, т. е. число Рейнольдса
Таблица 2 - Поправочные коэффициенты для расширения применимости закона Стокса
| | формула | примечания |
| Закон Стокса в общем виде | | F – сила (дин), μ – вязкость среды (П), ν – относительная скорость воздуха и частицы (см/с), и d – диаметр сферы (см). |
| При малом размере частиц (приближенном к молекулярным) | | Коэффициент сопротивления Милликена |
| При низкой вязкости среды | | Применяется при значениях числа Рейнольдса до 5 |
| Для капель жидкости | 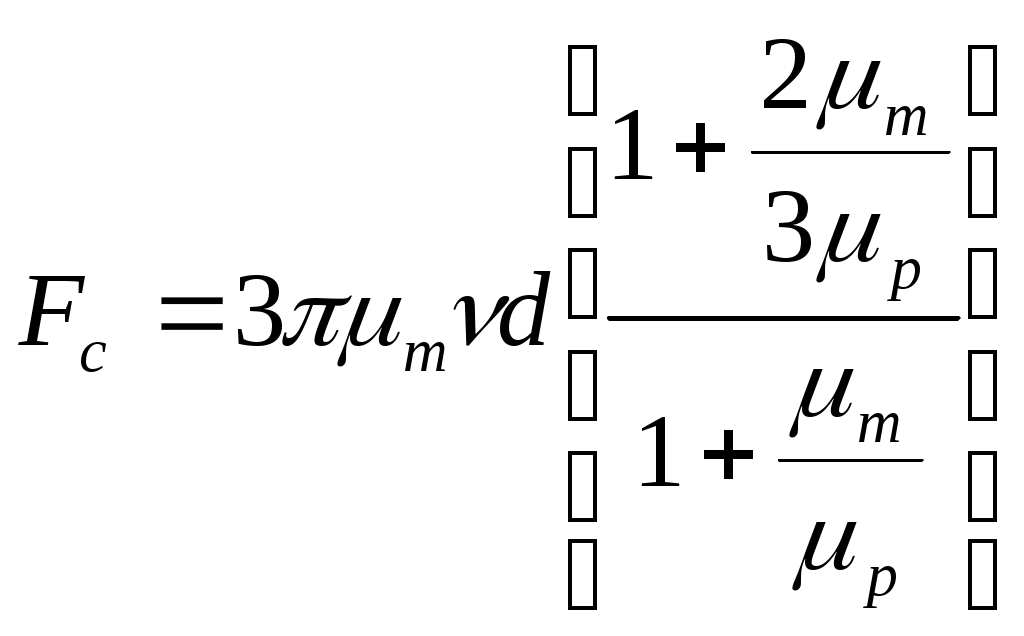 | |
| Для частиц несферической формы (цепочки, хлопья) | | к – поправочный динамический коэффициент формы, |
4.2 Броуновское движение и диффузия
Частицы могут выводиться из аэрозольной системы двумя путями: 1) они способны коагулировать (агрегировать) с другими частицами и укрупняться до таких размеров, что будут интенсивно оседать на поверхности под действием силы тяжести; 2) могут мигрировать к поверхностям осаждения, ударяться о них и оставаться связанными с ними. Процессы, вследствие которых аэрозольные частицы перемещаются к поверхности либо друг к другу без действия на них внешних сил, называются диффузионными, а движение частиц в таких процессах – броуновским движением.
Также часто употребляется термин броуновская диффузия аэрозолей, он подразумевает перенос частиц из областей с большей их концентрацией в области с меньшей концентрацией.
Аэрозольные частицы, взвешенные в газе, беспорядочно перемещаются из-за соударений с молекулами газа. Можно сказать, что броуновское движение аэрозолей «проявляет» скрытое тепловое молекулярное движение. Это явление в 1828 году впервые наблюдал в жидкостях шотландский ботаник Броун, в честь которого оно и получило свое наименование. В 1881 году Бодашевский изучил броуновское движение аэрозолей и нашел, что оно подобно хаотическому движению молекул газа, постулируемому кинетической теорией.
Законы, описывающие броуновскую диффузию частиц
Аэрозольные частицы можно представить себе как один из компонентов многокомпонентной газовой смеси, тогда возможны и справедливы известные физические и математические аналогии с процессами диффузии в газах. Когда аэрозольные частицы однородно распределены в газе, броуновское движение будет изменять расположение отдельных частиц, но не ансамбля частиц как целого. Если же наблюдаются какие-либо неоднородности распределения частиц в пространстве, то броуновское движение будет способствовать выравниванию концентраций частиц в газе: из областей с высокими концентрациями они будут перемещаться в области с низкими концентрациями. Этот процесс диффузии частиц описывается теми же феноменологическими законами, что и процессы молекулярной диффузии – законами Фика.
Согласно первому закону Фика:
где J – плотность потока частиц (1/(м²·с)), n – числовая концентрация (1/м³),
(м²/с) – коэффициент броуновской диффузии частиц. Этот закон описывает процесс стационарной диффузии и формулируется следующим образом: плотность потока аэрозольных частиц через поверхность, нормальную к направлению переноса, пропорциональна градиенту концентрации частиц, взятому с обратным знаком.
Согласно второму закону Фика:
Он описывает процесс нестационарной диффузии частиц в пространстве и формулируется так: производная концентрации аэрозольных частиц по времени в данной точке пространства пропорциональна лапласиану концентрации в этой точке.
Законы Фика являются феноменологическими и не могут расшифровать структуру коэффициента броуновской диффузии
Теория броуновского движения Эйнштейна
В 1905-1906 гг. А. Эйнштейн опубликовал результаты, которые сегодня считаются основополагающими и классическими в теории броуновского движения аэрозольных частиц. В частности, им были получены выражения для среднего квадрата смещения частицы при ее броуновском движении и коэффициента броуновской диффузии частиц
Таблица 3 - Окончательные результаты теории Эйнштейна
| Средний квадрат смещения частиц при поступательном движении | | Среднее значение квадрата смещения частицы Смещение частицы при трехмерном движении |
| Коэффициент поступательной броуновской диффузии частиц | | В – подвижность частицы (скорость, приобретаемая частицей под действием единичной силы), Т – температура газа, к – постоянная Больцмана |
| Броуновское вращение частиц | | |