ВАЖНО ДЛЯ СТУДЕНТА!!!!
в 7,13,15 ответ не совпадает,

в 11 нет уравнения окружности в условии

в 9 ошибка в условии, иначе не получится ответ, условие подправлено 

Практическая работа по разделу 3
Выполните задания:

1. 
   Найдите при каком значении постоянной С прямая линия, заданная уравнением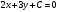 , отсекает на осях оХ и оУ отрезки а=3 и в=2 соответственно.
   

Уравнением прямой в отрезках называется уравнение вида



В нашем случае уравнение имеет вид : 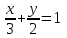. Умножим на 6 обе части уравнения: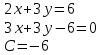



Ответ: С=-6

2. 
   Составить уравнение прямой L (в виде пересечения двух плоскостей), являющейся проекцией прямой А, заданной уравнением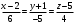 , на плоскость P, заданную уравнением x-3y+2z-7=0.
   

Искомая проекция L является прямой, по которой плоскость Р пересекается с плоскостью Q(проведенной через L перпендикулярно Р). Плоскости Q принадлежит точка (2,-1,5), вектор (6,-5,4) и нормальный вектор плоскости проекции (1,-3,2). Тогда получим



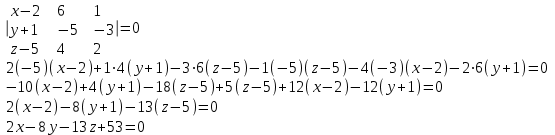
Тогда уравнение искомой проекции :

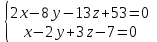
Ответ:

3. 
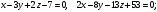
   На плоскости даны точки L(-6,0) и N(0,8). Найдите уравнение прямой, проходящей через середину отрезкаLN и отсекающей на оси ОХ втрое больший отрезок, чем на оси ОУ.
   

Найдем середину отрезка LN:

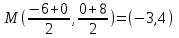
Уравнением прямой в отрезках называется уравнение вида



В нашем случае

---

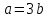
. Подставим также точку М:



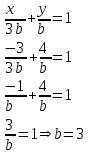
Тогда искомое уравнение:



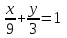
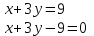
Ответ:

4. 
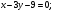
   На плоскости точки P(0,5), Q(-3,1), R(1,-2) являются вершинами треугольника. Найдите длину высоты треугольника, опущенной из вершины R.
   

Уравнение прямой PQ
Каноническое уравнение прямой:

или

или
y = ⁴/₃x + 5 или 3y -4x - 15 = 0

Длина высоты треугольника, проведенной из вершины R
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины:

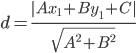
Найдем расстояние между точкой R(1;-2) и прямой PQ (3y -4x - 15 = 0)



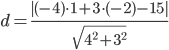
Ответ:5

5. 
   Найдите каноническое уравнение кривой на плоскости, заданной уравнением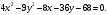
   

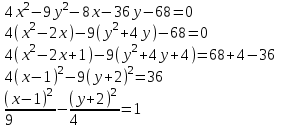
Ответ:

6. 
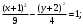
   Найдите уравнения касательных к окружности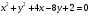 , проходящих через начало координат.
   

---

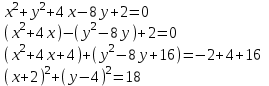
Пусть k — угловой коэффициент искомой касательной. Тогда уравнение касательной имеет вид y - 0 = k(x - 0), или y = kx . Данная задача сводится к нахождению всех таких чисел k, для которых система уравнений



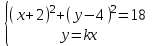
имеет ровно одно решение

Подставим второе уравнение в первое:


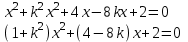
Это уравнение имеет единственное решение тогда и только тогда, когда его дискриминант равен 0, т.е



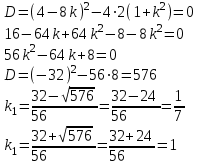
В результате получим уравнения

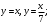
Ответ:

7. 
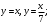
   Найдите каноническое уравнение эллипса, симметричного относительно координатных осей и проходящего через точк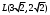и и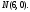
   

Уравнение эллипса с центром в точке (0,0) имеет вид:



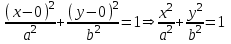
Подставим имеющиеся точки и решим систему уравнений:





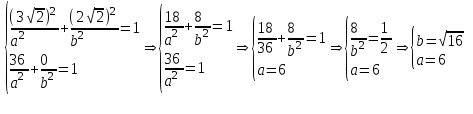
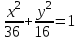
_Ответ:

8. 
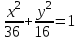
   Известны координаты вершин тетраэдра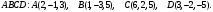 Найдите длину высоты, опущенной из вершины 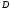на грань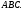
   

Расстояние d от точки M₁(x₁;y₁;z₁) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:

---

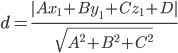
Уравнение плоскости ABC найдем как уравнение плоскости по трем точкам:







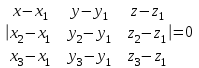
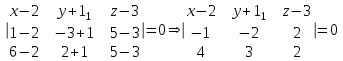
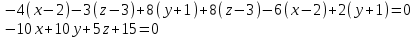
-2x + 2y + z + 3 = 0– уравнение плоскости ABC

Тогда

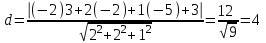
Ответ: d=4

9. 
   Напишите уравнение окружности, проходящей через три точки: (0,1), (2,0) , (3,-1).
   

Искомое уравнение имеет вид (x - a)² + (y - b)² = r². Поскольку окружность проходит через заданные точки, координаты каждой из этих точек удовлетворяют уравнению окружности. Подставляя поочередно в искомое уравнение координаты данных точек, получим три уравнения для определения a, b и r. Вот эти уравнения:



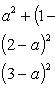
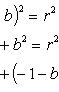
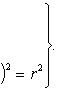
Возьмем уравнения первое и второе, а потом первое и третье. Правые части этих уравнений между собой равны, значит, равны и левые их части, и мы получаем



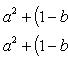
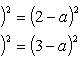
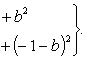
Раскрывая скобки и упрощая, будем иметь



Отсюда 

---

. Подставляя эти значения a и b в первое из уравнений системы, получим  . Искомое уравнение имеет вид



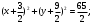
Ответ:

10. 
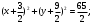
    Найдите длины полуосей 2а и 2в, координаты фокусов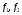 и эксцентриситет эллипса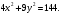
    

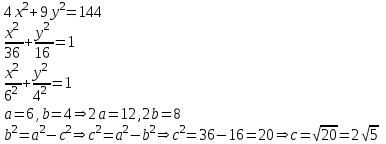
Координаты фокусов эллипса имеют вид (-с,0), (с,0).

Значит .

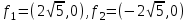Эксцентриситет равен

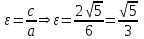
Ответ:

11. 
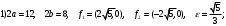
    Найдите уравнения прямой, параллельной оси абсцисс и пересекающей окружность в таких точках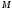 и 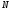что длина отрезка 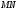равна 1.
    

12. 
    Найдите уравнения касательных к гиперболе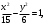 параллельных прямой .
    

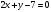Если уравнения касательных параллельны прямой 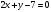_{, то их уравнения будут иметь вид} .

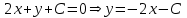Подставим это уравнение в уравнение гиперболы:



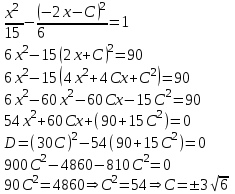
Значит, уравнения касательных к гиперболе имеют вид

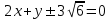
Ответ:

13. 
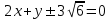
    Найдите точку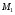 симметричную точке 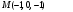относительно прямой .
    

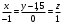Найдем уравнение плоскости, перпендикулярной прямой:

---

Смотрите также файлы

• Информационная среда организации это.docx

• Изложение бизнес идеи.docx

• Пути и способы введения лекарственных средств в организм.pdf

• Инструкция по монтажу и эксплуатации 9 Введение 9 Общие указания 9 Указание мер безопасности 10 Порядок установки.pdf

• Исследование электронного осциллографа.docx