Файл: Практическая работа по разделу 3 Выполните задания.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 247
Скачиваний: 17
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
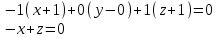
Найдем точку пересечения прямой и плоскости.
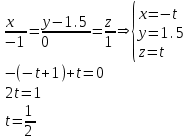
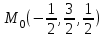- координаты точки пересечения.Отсюда,
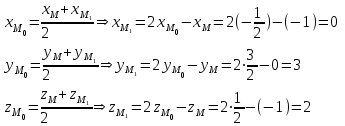
Следовательно,
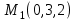- искомая точка.Ответ:
-
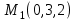
Найдите точку пересечения прямой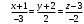
и плоскости
.
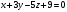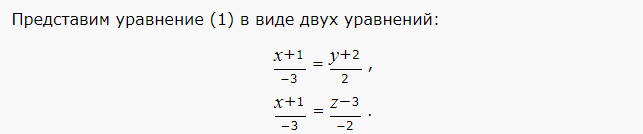
Сделаем перекрестное умножение в уравнениях
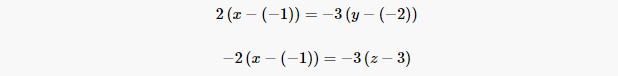
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
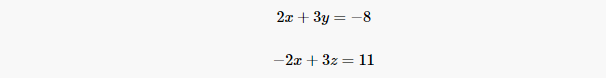
Для нахождения точки пересечения прямой и плоскости нужно решить совместно эти уравнения . Для этого переведем в уравнении свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений.
Для решения системы по правилу Крамера найдем следующие определители:
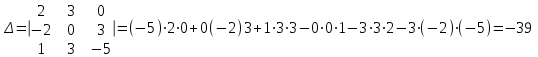
Так как данный определитель не равен нулю, то данная система имеет единственное решение, а значит система совместна.
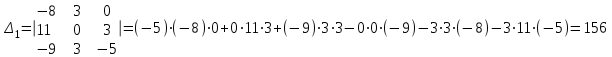
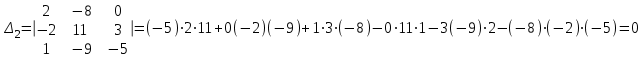
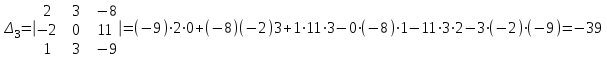
Тогда решение системы находим по формулам:
x
=
= 
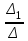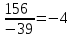; y= 
= 
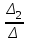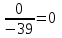; z =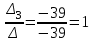 
Ответ: (-4,0,1)
-
Найдите уравнение плоскости, проходящей через точку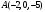
перпендикулярно вектору 
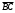, есл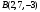и 
и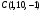 
.
Чтобы составить уравнение плоскости, зная координаты точки плоскости M(x0, y0, z0) и вектора нормали плоскости n= {A; B; C} можно использовать следующую формулу.
A(x - x0) + B(y - y0) + C(z - z0) = 0
n=(1-2;10-7;-1+3)=(-1;3;2)
Тогда уравнение плоскости будет иметь вид:
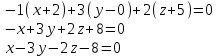
Ответ:
-
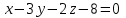
Вычислить объем тетраэдра с вершинами в точках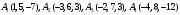
.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
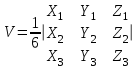
A1A2 =(-3-1;6-5;3+7)=(-4;1;10)
A1A3 =(-2-1;7-5;3+7)=(-3;2;10)
A1A4 =(-4-1;8-5;-12+7) =(-5;3;-5)
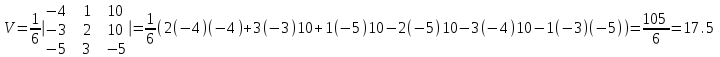
Ответ: 17.5
Ответы
1.-6
2.
3.
4. h=5;
5.
6.
8. d=4
9.
10
11.
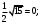
12.
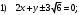
13.
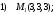
14.
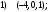
15.
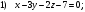
16.
