(с начала 30-х годов интерес к соответствующей проблематике был проявлен многими учеными, перечень работ см. в [Грин, 1966]).

Алгоритм построения шкалы Лайкерта предусматривает про­ведение некоторого пилотажного исследования, цель которого — отбор таких признаков, значения которых коррелируют с суммой значений всех остальных. Именно такие признаки предлагается включать в анкету, предназначенную для проведения основного исследования. Упомянутая корреляция и позволяет обеспечить по­ложительные ответы на три первых упомянутых выше вопроса. Прежде чем показать это, остановимся на вопросе о том, что зна­чит "признаки коррелируют".

Вычислив коэффициент корреляции между рангами проверяе­мого признака и суммой рангов всех остальных признаков, оце­ним, является ли он достаточно большим для того, чтобы можно было говорить о наличии соответствующей связи. Для этого зада­димся каким-то пороговым значением: будем считать, что если этот коэффициент больше 0,8, то связь есть, если меньше — то ее нет. Подчеркнем, что здесь мы имеем дело с довольно типичной для социологии ситуацией, когда задание порогового критерия является чисто субъективным делом исследователя и обоснование соответствующего выбора может опираться только на эмпиричес­кий опыт социолога. Перейдем к обещанному рассмотрению того, как в рассматриваемом случае реализуется тестовая традиция.

Первый вопрос — о существовании одномерной латентной переменной. После указанного отбора останутся только такие наблюдаемые признаки, каждый из которых коррелирует с сум­мой остальных. Это означает, что для измерения латентной пе­ременной будут использованы такие наблюдаемые, которые об­разуют связанный "пучок". В соответствии с приведенными в конце п. 7.4 соображениями это дает основание полагать, что за наблюдаемыми переменными действительно скрывается некий латентный фактор.

Можно показать, что при фиксации значения латентной пе­ременной (т.е. при рассмотрении только таких респондентов, для которых сумма баллов, приписанных ими рассматриваемым суждениям, будет одна и та же), связь между наблюдаемыми переменными пропадает. Таким образом, мы можем считать, что гипотетический латентный фактор действительно обуслов­ливает наблюдаемые связи.

Второй вопрос — о выборе адекватных наблюдаемых призна­ков. Та же связь, о которой мы только что говорили, свидетель­ствует и о том, что наши наблюдаемые переменные имеют отно­шение к одной и той же латентной.

---

Как мы уже отмечали, решая вопрос о том, те ли наблюдаемые переменные мы берем для того, чтобы через них выражать интере­сующий нас латентный фактор, необходимо убедиться не только в том, что эти переменные отвечают задаче по самой своей сути (по своему наименованию), но и в том, что они измерены именно так, как надо. Лайкерт задумывался о том, корректна ли традици­онная пятичленная шкала. Сначала он пытался использовать под­ход, в наше время называемый методом оцифровки (об оцифров­ке см., например, [Интерпретация и анализ..., гл. 3, 4]), респон­дентам, давшим ответы "вполне согласен "."согласен" и т.д., при­писывают не баллы 5, 4 и т.д., а некоторые числа, подобранные таким образом, чтобы результирующее частотное распределение было нормальным (напомним, что в соответствии с формальными требованиями ФА распределение значений каждого количествен­ного наблюдаемого признака должно быть нормальным [Интер­претация и анализ..., с. 218]). Но потом удалось экспериментально доказать, что две результирующие шкалы (обе измеряющие нашу латентную переменную), одна — полученная на основе суммиро­вания описанных выше пятибалльных оценок, а другая — на осно­ве суммирования оценок-результатов описанной оцифровки, очень сильно коррелируют друг с другом. Если считать, что наше измере­ние латентной переменной отвечает порядковой шкале, то указан­ного обстоятельства оказывается достаточно для того, чтобы счи­тать такие шкалы идентичными (большая корреляция говорит о сходстве порядков шкальных значений, полученных по нашим шка­лам). Значит, имеет смысл пользоваться именно пятибалльной — более простой. К определению типа шкалы Лайкерта вернемся поз­же, пока будем считать ее порядковой.

Третий вопрос — о форме выражения латентной переменной через наблюдаемую. То, что о суммарной связи в рассматриваемом "пучке" наблюдаемых признаков мы судили по наличию корреля­ции между каждым признаком и суммой всех остальных, косвенно свидетельствует о пригодности именно суммы значений наблюда­емых признаков в качестве значения латентной переменной.

Имеется и более серьезное обоснование целесообразности сум­мирования результатов измерения наблюдаемых переменных. Оно базируется на изучении однофакторной модели ФА: на анализе тенденций изменения корреляции между латентным общим фак­тором и суммой баллов наблюдаемых признаков при стремле­нии количества таких признаков к бесконечности (соответству­ющие ссылки можно найти в названной выше работе Грина). Мы не будем рассматривать этот вопрос более подробно, по­скольку он требует достаточного погружения в математику. Кон­статируем только, что это лишний раз демонстрирует нам роль математики в эмпирической социологии.

---

Ради объективности следует также заметить, что имеются ра­боты, в которых высказываются серьезные сомнения в право­мерности обсуждаемой аддитивной модели по отношению к кон­кретным латентным переменным (так, в [Сознание и трудовая..., 1985] именно в таком ракурсе рассматривается проблема изме­рения удовлетворенности человека своим трудом).

Перейдем к рассмотрению нашего четвертого вопроса — о типе получающейся шкалы. Представляется очевидной ее поряд-ковость. Однако нередко имеется возможность полагать, что она интервальна. Попытаемся это обосновать. Соответствующие рас­суждения близки к тем, с помощью которых мы доказывали интервальность установочной шкалы Терстоуна.

Наш порядковый признак может принимать большое коли­чество значений (если, скажем, у нас 10 суждений, то суммар­ный балл изменяется от 10 до 50). Человеку трудно дифференци­ровать свои представления о таком количестве качественно раз­личных состояний латентной переменной. И даже если расстоя­ния между соседними баллами не равны, этим можно пренеб­речь, поскольку соответствующие различия будут очень малы с точки зрения возможности их четкой содержательной интер­претации. Будем поэтому считать их одинаковыми. Тем самым будем воспринимать шкалу как интервальную.

Описанная идея Лайкерта очень схожа с идеями, заложенны--ми в ФА. Отличие состоит в том, что: 1) здесь заведомо предпо­лагается, что фактор только один (в ФА количество факторов не задается априори, а определяется характером статистических дан­ных); 2) исходные признаки измеряются по порядковой шкале, соответствующая информация легко может быть получена от рес­пондента (ФА, как мы говорили, предполагает интервальность исходных шкал); 3) анализ корреляционной матрицы (анализ совокупной корреляции всех признаков друг с другом) заменя­ется оценкой силы корреляции каждого из них с суммой значе­ний всех остальных; 4) значение фактора определяется как сум­ма значений наблюдаемых переменных (в линейном ФА задей­ствована взвешенная сумма; веса определяются характером дан­ных и несут содержательный смысл, помогают интерпретиро­вать найденные факторы). Можно сказать, что шкала Лайкерта в описанном варианте представляет собой эвристический, легко реализуемый "вручную" (без использования ЭВМ) и опираю­щийся на сравнительно легко получаемую от респондента ин­формацию, подход, который в более серьезном, опирающемся на строгие математические гипотезы, виде заложен в ФА.
7.5.2.

---

ШкалограммаГуттмана

Известный американский психолог Л.Гуттман предложил свой способ адаптации тестовой традиции к потребностям социоло­гии [Guttman, 1950]. В принципе идея была той же — опереться на проверку того, что наблюдаемые признаки представляют со­бой плотную "связку" в смысле корреляции друг с другом, и предложить такой способ измерения латентной переменной, чтобы при фиксации ее значения эти корреляции исчезали. Опи­сание метода можно найти в [Грин, 1966; Гуттман, 1966; Оси­пов, Андреев, 1977; Рабочая книга..., 1983; Ядов, 1995].

Наблюдаемые признаки — дихотомические. Предполагается, что выполнение условий, требующихся для реализации тесто­вой традиции, будет обеспечено, если удастся доказать возмож­ность определенным образом их упорядочить. А именно: будем говорить, что признаки упорядочены, если, скажем, относи­тельно человека, положительно реагирующего на третий при­знак, можно быть почти уверенным, что он положительно реа­гировал и на четвертый, пятый и т.д. признаки.

Подобные шкалы называются кумулятивными. Они использо­вались и до Гуттмана. Так, кумулятивна известная шкала социаль­ной дистанции Богардуса, содержащая семь признаков, отража­ющих различные степени социальной дистанции. Эти признаки могут быть следующим образом упорядочены (речь идет об отно­шении респондента к человеку или социальной группе, дистан­ция до которой вычисляется): допущение человека в качестве род­ственника посредством брака, как личного друга, в качестве сосе­да, допущение равной работы, гражданства, допущение в страну только в качестве туриста. Кумулятивность шкалы представляется очевидной: относительно респондента, согласного принять кого-то в качестве соседа, можно почти наверняка сказать, что он согласится с тем, чтобы тот же человек имел одинаковые с ним работу, гражданство, или мог приехать в страну как турист.

Значение латентной переменной рассчитывается как сумма положительных ответов, данных респондентом на рассматрива­емые вопросы. Нетрудно показать, что если рассматриваемые дихотомические признаки удалось упорядочить, то соответству­ющая матрица данных приведется к так называемому диагональ­ному виду (табл. 7.2).



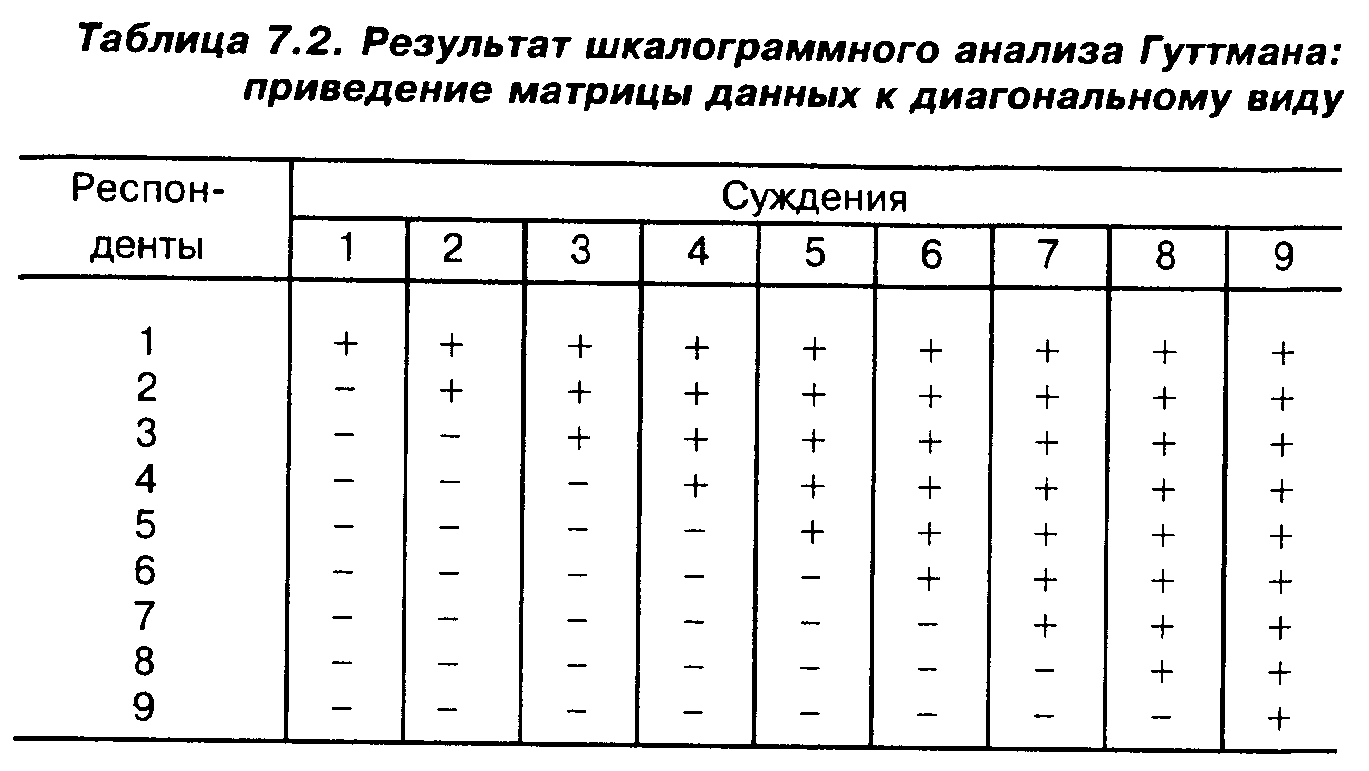
Плюсами помечены положительные ответы респондентов на соответствующие вопросы анкеты (их согласие с соответствую­щими суждениями), минусами — отрицательные.

---

Нетрудно проверить, что согласие респондента, скажем, с 4-м суждением означает его согласие с 5-м, 6-м и т.д. А это и означа­ет, что наши признаки упорядочены.

Но поскольку количество респондентов, как правило, будет больше числа суждений, то многие респонденты будут давать одинаковые наборы ответов, и матрица приобретет ступенчато-диагональный вид (табл. 7.3).

Нетрудно показать, что для таких переменных будут выпол­нены все требующиеся посылки: они будут связаны друг с дру­гом и фиксация значения латентной переменной приведет к распаду этих связей.

Действительно, пусть р.ир.—вероятности положительных от­ветов на /-й и у'-й вопросы соответственно, р.. — вероятность по­ложительного ответа на /-й и у'-й вопросы одновременно (напом­ним, что в выборочном исследовании вероятность какого-либо события отождествляется с относительной частотой его встречае­мости).

Таблица 7.3. РезультатшкалограммногоанализаГуттмана: приведениематрицыданныхкступенчато-диагональному

виду

Респон­денты	Суждения									Значение латентной переменной
	1	2	3	4	5	6	7	8	9
1	+	+	+	+	+	+	+	+	+	9
2	+	+	+	+	+	+	+	+	+	9
3	+	+	+	+	+	+	+	+	+	9
4	-	+	+	+	+	+	+	+	+	8
5	-	-	+	+	+	+	+	+	+	7
6	-	-	+	+	+	+	+	+	+	7
7	-	-	-	+	+	+	+	+	+	6
8	-	-	-	+ .	+	+	+	+	+	6
9	-	-	-	+	+	+	+	+	+	6
10	-	-	-	-	+	+	+	+	+	5
11	-	-	-	-	+	+	+	+	+	5
12						+	+	+	+	4
13							+	+	+	3
14								+	+	2
15								+	+	2
16								+	+	2
17									+	1
18										1

---

Смотрите также файлы

• Методические указания по решению задач есть в Методических указаниях по выполнению самостоятельных и контрольных работ для заочников (стр. 2639).docx

• 1 Основные принципы и методы практики. Польза и эффекты цигуна на организм.docx

• Построение и использование компьютерных моделей.docx

• Реферат введение Географоэкономическая характеристика района работ.docx

• Коррупция и ее типы, виды, модели.docx