ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 340
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Stи оба имеют одинаковую размерность, R2отвечает отношению S2с той же размерностью, Rm — отношению Sm.
Назовем гомоморфизмом такое отображение 21 в 23 (символически — И:21 —► 23), при котором каждому объекту из Аставится в соответствие один элемент из В (разным элементам из А может отвечать один и тот же элемент из В)так, что для любого / какие
то объекты из А вступают в некоторое отношение Я тогда и только тогда, когда их образы из Ввступают в отношение S..
Изоморфизм — частный случай гомоморфизма, отличается от последнего тем, что отображение А в В не только однозначно, но и взаимнооднозначно.
Пусть21 — ЭСО, а© — ЧСО. Шкалой будем называть гомоморфное отображение к.21 —►ЯЗ.
Если А — это множество респондентов с заданными на нем отношениями равенства и порядка по росту, а В — множество натуральных чисел с заданными на нем обычными числовыми отношениями равенства и порядка и эмпирические отношения равенства и порядка ставятся нами в соответствие одноименным числовым отношениям, то осуществление гомоморфного отображения из 21 в 23 обозначает, что каждому респонденту ставится в соответствие некоторое число таким образом, что равным по росту респондентам отвечают одинаковые числа, более высокому респонденту отвечает большее число.
Преобразование φ называется допустимым преобразованием шкалы, если из того, что к.21 —►© — шкала, следует, что к.21 —►23'= = < φ (В), SrS>—тоже шкала. При этом к=φ » h—суперпозиция функций φ и И.Ее использование означает последовательное применение /гиф.
Отметим, что социологи часто негативно реагируют на использование терминов "изоморфизм" и "гомоморфизм" при описании процесса измерения, считая их чисто математическими. Вряд ли такой подход правилен. Эти термины активно задействованы в литературе по осмыслению понятия модели [Гастев, 1972] и процесса познания [Frey, 1969].
13.3.3. ТипологияшкалпоСтивенсу
Исходя из сказанного выше, будем отождествлять тип шкалы с совокупностью отвечающих ей допустимых преобразований.
Нетрудно понять, что допустимыми преобразованиями знакомых нам номинальной, порядковой и интервальной шкал являются преобразования, указанные в табл. 13.1. Там же определены допустимые преобразования пока не использованных нами шкал — разностей, отношений и абсолютной. Задав допустимые преобразования этих шкал, мы тем самым их определили.
Перейдем к вопросу о сравнении введенных типов шкал.
Назовем тип одной шкалы более высоким, чем тип другой, если совокупность допустимых преобразований первой шкалы включается в совокупность допустимых преобразований второй. Смысл такого определения ясен: принадлежащими к более высокому типу мы считаем такие шкалы, для которых соответству-. ющие шкальные значения являются более устойчивыми, меньше могут "болтаться", т.е. больше похожи на настоящие числа. Ясно, что к более устойчивым шкалам можно применять большее количество математических методов.
Если принять это определение, то между всеми типами шкал можно установить соответствующее отношение порядка. Но это отношение будет частичным. Нетрудно видеть, что несравнимыми оказываются шкалы отношений и шкалы разностей: ни одна из соответствующих совокупностей допустимых преобразований не включается в другую.
Частично упорядоченное множество можно изобразить в виде математической решетки. Мы не будем строго определять это понятие. Надеемся, что читателю будет примерно ясно, о чем идет речь, если мы скажем, что в нашем случае эта решетка будет иметь вид, изображенный на рис. 13.1 (более высокому типу шкал отвечает более высоко расположенный прямоугольник).
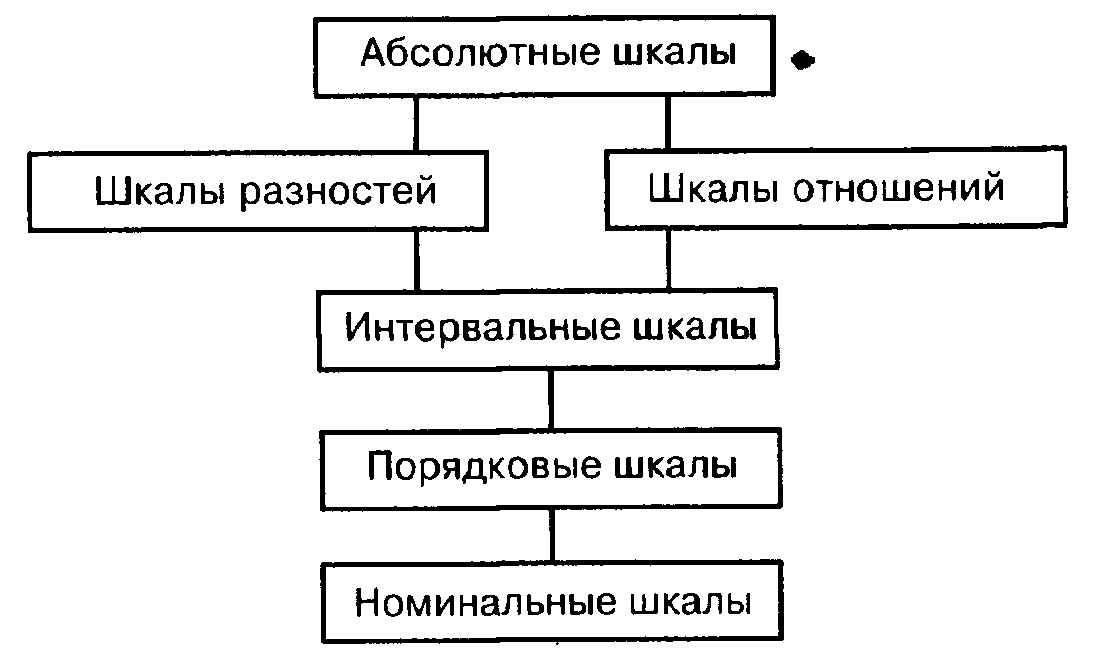
Рис. 13.1. Частичноупорядоченноемножествотиповшкал, наиболеечастоиспользующихсявсоциологических
исследованиях
Заметим, что в рамках РТИ существуют и другие подходы к пониманию сравнимости разных типов шкал. Их описание можно найти в [Высоцкий, 1978].
13.3.4. Практическаявозможностьпостроенияшкал
Покажем, что все эти шкалы действительно нередко встречаются в социологических исследованиях. Будем надеяться, что относительно номинальных и порядковых шкал у читателя сомнений не возникает.
Наиболее типичные способы получения интервальной шкалы фактически описаны выше. При обсуждении разных методов одномерного шкалирования мы анализировали, почему получающиеся шкалы можно считать интервальными. Речь шла не о непосредственном построении гомоморфного отображения ЭСО в ЧСО. Более того, мы даже не задавались целью измерять те отношения, которые специфичны именно для интервальной шкалы, — отношения равенства или порядка между интервалами (расстояниями). Вместо этого предполагалось, что для ЭС выполняется целая совокупность свойств, связанных в первую очередь с моделью восприятия. Эти свойства выражались в терминах используемой ЧС. Другими словами, мы прибегали к таким предположениям о характере ЭС, которые в п. 3.1 были названы дополнительными.
В литературе доказывается, что некоторые известные методы шкалирования позволяют получить шкалы разностей и шкалы отношений (например, это касается ряда методов парных сравнений; примеры можно найти в [Суппес, Зинес, 1967]).
Можно привести и более естественные подходы к получению шкал двух последних типов. Мы имеем в виду привычные всем способы, опирающиеся на использование единицы измерения и на существование некоторого начала отсчета (эти способы охватываются классификацией Стивенса).
Ясно, что в процессе измерения физических величин при фиксации начала отсчета и изменении единицы измерения мы получаем шкалу отношений. Пример — шкала весов: измерив веса каких-то предметов в килограммах, мы можем получить те же веса в центнерах, пудах, фунтах путем умножения первоначальных весов всех предметов одновременно на подходящий множитель. А это и есть преобразование подобия.
Шкала разностей получается, например, в том случае, когда у нас фиксируется единица измерения, но может изменяться начало отсчета. Она реже встречается в реальной жизни. Но все же и здесь можно привести пример. У европейских народов возраст человека измеряется в годах от момента появления человека на свет из утробы матери. А в Монголии измерение возраста происходит по-другому. Чтобы получить "монгольский" возраст любого человека, надо к "европейскому" прибавить 9 месяцев. Перевод совокупности возрастов какой-либо совокупности людей из одной системы расчетов в другую — это преобразование сдвига. Другими словами, мы имеем дело со шкалой разностей (если говорить не только о людях, но о
других животных с разными сроками беременности, то сдвиги будут различными).
Даже абсолютные шкалы встречаются в социологии, хотя на первый взгляд это кажется невероятным: ведь для этой шкалы числа являются полноценными числами, "прибитыми гвоздями" к числовой оси, а мы уже не раз говорили, что числа мало пригодны для адекватного отображения интересующей социолога реальности.
Итак, примеры абсолютой шкалы. Во-первых, такую шкалу дают результаты счета. Предположим, что мы исследуем эффективность изучения иностранного языка в зависимости от количества учеников в группе. Ясно, что нашим измеряемым объектам — группам — будут приписаны числа именно по абсолютной шкале: каждой группе будет поставлено в соответствие число ее членов и уж здесь замена, скажем, чисел 5 и 25 какими-либо другими будет лишена всякого содержательного смысла.
Во-вторых, социолог иногда пользуется так называемым измерением "по приказу", когда респондент по заданию социолога сам приписывает число себе или какому-либо объекту. Типичным примером такого измерения является графическая оценка объектов, о которой мы говорили в п. 11.1 при обсуждении второй классификации Кумбса. Конечно, в такого рода данных мы можем весьма сомневаться. Но если уж мы идем на использование подобной оценки, то, значит, верим респондентам. В таком случае изменения получающихся чисел тоже выглядят недопустимыми.
Глава 14. РЕПРЕЗЕНТАЦИОННАЯ ТЕОРИЯ ИЗМЕРЕНИЙ (РТИ) С ТОЧКИ ЗРЕНИЯ ПОТРЕБНОСТЕЙ СОЦИОЛОГИИ
Как мы уже отмечали, РТИ нельзя считать полностью отвечающей потребностям социологии. В ней отсутствуют многие элементы, без которых невозможно создание теории социологического измерения. Это связано, по большому счету, с тем, что предметом ее изучения не являются ЭС. Ее утверждения исходят из того, что ЭС задана. А ведь для социолога определение вида ЭС — один из самых сложных вопросов. Кроме того, социологические ЭС далеко не всегда имеют свойства, хотя бы отдаленно похожие на свойства чисел. В данной главе мы подробнее рассмотрим, что может дать социологу РТИ. Прежде всего покажем, какова та полезная роль, которую может сыграть рассматриваемый формализм в социологическом исследовании, и чего в этом формализме социологу заведомо не хватает.
14.1. Основные задачи, решаемые РТИ
Начнем с перечисления тех полезных для социолога результатов, которые содержатся в РТИ. Эти результаты сводятся к возможности решения следующих задач.
1. Доказательство существования шкал.
РТИ содержит много результатов, имеющих примерно такую формулировку: если ЭС обладает такими-то свойствами (при этом она может быть определена и не в виде ЭСО; в качестве "свойств" может выступать, например, требование адекватности одной из рассмотренных выше моделей восприятия), то ее можно гомоморфно отобразить в ЧСО. Подобные утверждения, несомненно, могут быть весьма полезны. Другое дело, что упомянутое "если" может быть весьма проблематичным для социолога.
2. Определение степени единственности шкалы.
Обосновав возможность построения шкалы в рамках РТИ, обыч-
но показывают, с какой точностью определены получившиеся
шкальные значения. По существу это сводится к доказательству того, что получившаяся шкала является шкалой такого-то типа.
Подчеркнем, что именно в рамках РТИ было доказано, что с помощью ряда конкретных методов шкалирования получаются шкалы определенного типа. Это касается, например, многих методов парных сравнений, в частности тех, которые были рассмотрены в п. 6.
3. Проблема адекватности математического метода и ее решение в теории измерений.
Проблема адекватности является центральной для РТИ. Описанное выше стремление ученых к выработке четких представлений о том, что есть измерение в гуманитарных науках, было направлено в основном на решение вполне практической задачи — понять,
Назовем гомоморфизмом такое отображение 21 в 23 (символически — И:21 —► 23), при котором каждому объекту из Аставится в соответствие один элемент из В (разным элементам из А может отвечать один и тот же элемент из В)так, что для любого / какие

то объекты из А вступают в некоторое отношение Я тогда и только тогда, когда их образы из Ввступают в отношение S..
Изоморфизм — частный случай гомоморфизма, отличается от последнего тем, что отображение А в В не только однозначно, но и взаимнооднозначно.
Пусть21 — ЭСО, а© — ЧСО. Шкалой будем называть гомоморфное отображение к.21 —►ЯЗ.
Если А — это множество респондентов с заданными на нем отношениями равенства и порядка по росту, а В — множество натуральных чисел с заданными на нем обычными числовыми отношениями равенства и порядка и эмпирические отношения равенства и порядка ставятся нами в соответствие одноименным числовым отношениям, то осуществление гомоморфного отображения из 21 в 23 обозначает, что каждому респонденту ставится в соответствие некоторое число таким образом, что равным по росту респондентам отвечают одинаковые числа, более высокому респонденту отвечает большее число.
Преобразование φ называется допустимым преобразованием шкалы, если из того, что к.21 —►© — шкала, следует, что к.21 —►23'= = < φ (В), SrS>—тоже шкала. При этом к=φ » h—суперпозиция функций φ и И.Ее использование означает последовательное применение /гиф.
Отметим, что социологи часто негативно реагируют на использование терминов "изоморфизм" и "гомоморфизм" при описании процесса измерения, считая их чисто математическими. Вряд ли такой подход правилен. Эти термины активно задействованы в литературе по осмыслению понятия модели [Гастев, 1972] и процесса познания [Frey, 1969].
13.3.3. ТипологияшкалпоСтивенсу
Исходя из сказанного выше, будем отождествлять тип шкалы с совокупностью отвечающих ей допустимых преобразований.
Нетрудно понять, что допустимыми преобразованиями знакомых нам номинальной, порядковой и интервальной шкал являются преобразования, указанные в табл. 13.1. Там же определены допустимые преобразования пока не использованных нами шкал — разностей, отношений и абсолютной. Задав допустимые преобразования этих шкал, мы тем самым их определили.
Перейдем к вопросу о сравнении введенных типов шкал.
Назовем тип одной шкалы более высоким, чем тип другой, если совокупность допустимых преобразований первой шкалы включается в совокупность допустимых преобразований второй. Смысл такого определения ясен: принадлежащими к более высокому типу мы считаем такие шкалы, для которых соответству-. ющие шкальные значения являются более устойчивыми, меньше могут "болтаться", т.е. больше похожи на настоящие числа. Ясно, что к более устойчивым шкалам можно применять большее количество математических методов.
Если принять это определение, то между всеми типами шкал можно установить соответствующее отношение порядка. Но это отношение будет частичным. Нетрудно видеть, что несравнимыми оказываются шкалы отношений и шкалы разностей: ни одна из соответствующих совокупностей допустимых преобразований не включается в другую.
Частично упорядоченное множество можно изобразить в виде математической решетки. Мы не будем строго определять это понятие. Надеемся, что читателю будет примерно ясно, о чем идет речь, если мы скажем, что в нашем случае эта решетка будет иметь вид, изображенный на рис. 13.1 (более высокому типу шкал отвечает более высоко расположенный прямоугольник).

Рис. 13.1. Частичноупорядоченноемножествотиповшкал, наиболеечастоиспользующихсявсоциологических
исследованиях
Заметим, что в рамках РТИ существуют и другие подходы к пониманию сравнимости разных типов шкал. Их описание можно найти в [Высоцкий, 1978].
13.3.4. Практическаявозможностьпостроенияшкал
Покажем, что все эти шкалы действительно нередко встречаются в социологических исследованиях. Будем надеяться, что относительно номинальных и порядковых шкал у читателя сомнений не возникает.
Наиболее типичные способы получения интервальной шкалы фактически описаны выше. При обсуждении разных методов одномерного шкалирования мы анализировали, почему получающиеся шкалы можно считать интервальными. Речь шла не о непосредственном построении гомоморфного отображения ЭСО в ЧСО. Более того, мы даже не задавались целью измерять те отношения, которые специфичны именно для интервальной шкалы, — отношения равенства или порядка между интервалами (расстояниями). Вместо этого предполагалось, что для ЭС выполняется целая совокупность свойств, связанных в первую очередь с моделью восприятия. Эти свойства выражались в терминах используемой ЧС. Другими словами, мы прибегали к таким предположениям о характере ЭС, которые в п. 3.1 были названы дополнительными.
В литературе доказывается, что некоторые известные методы шкалирования позволяют получить шкалы разностей и шкалы отношений (например, это касается ряда методов парных сравнений; примеры можно найти в [Суппес, Зинес, 1967]).
Можно привести и более естественные подходы к получению шкал двух последних типов. Мы имеем в виду привычные всем способы, опирающиеся на использование единицы измерения и на существование некоторого начала отсчета (эти способы охватываются классификацией Стивенса).
Ясно, что в процессе измерения физических величин при фиксации начала отсчета и изменении единицы измерения мы получаем шкалу отношений. Пример — шкала весов: измерив веса каких-то предметов в килограммах, мы можем получить те же веса в центнерах, пудах, фунтах путем умножения первоначальных весов всех предметов одновременно на подходящий множитель. А это и есть преобразование подобия.
Шкала разностей получается, например, в том случае, когда у нас фиксируется единица измерения, но может изменяться начало отсчета. Она реже встречается в реальной жизни. Но все же и здесь можно привести пример. У европейских народов возраст человека измеряется в годах от момента появления человека на свет из утробы матери. А в Монголии измерение возраста происходит по-другому. Чтобы получить "монгольский" возраст любого человека, надо к "европейскому" прибавить 9 месяцев. Перевод совокупности возрастов какой-либо совокупности людей из одной системы расчетов в другую — это преобразование сдвига. Другими словами, мы имеем дело со шкалой разностей (если говорить не только о людях, но о
других животных с разными сроками беременности, то сдвиги будут различными).
Даже абсолютные шкалы встречаются в социологии, хотя на первый взгляд это кажется невероятным: ведь для этой шкалы числа являются полноценными числами, "прибитыми гвоздями" к числовой оси, а мы уже не раз говорили, что числа мало пригодны для адекватного отображения интересующей социолога реальности.
Итак, примеры абсолютой шкалы. Во-первых, такую шкалу дают результаты счета. Предположим, что мы исследуем эффективность изучения иностранного языка в зависимости от количества учеников в группе. Ясно, что нашим измеряемым объектам — группам — будут приписаны числа именно по абсолютной шкале: каждой группе будет поставлено в соответствие число ее членов и уж здесь замена, скажем, чисел 5 и 25 какими-либо другими будет лишена всякого содержательного смысла.
Во-вторых, социолог иногда пользуется так называемым измерением "по приказу", когда респондент по заданию социолога сам приписывает число себе или какому-либо объекту. Типичным примером такого измерения является графическая оценка объектов, о которой мы говорили в п. 11.1 при обсуждении второй классификации Кумбса. Конечно, в такого рода данных мы можем весьма сомневаться. Но если уж мы идем на использование подобной оценки, то, значит, верим респондентам. В таком случае изменения получающихся чисел тоже выглядят недопустимыми.
Глава 14. РЕПРЕЗЕНТАЦИОННАЯ ТЕОРИЯ ИЗМЕРЕНИЙ (РТИ) С ТОЧКИ ЗРЕНИЯ ПОТРЕБНОСТЕЙ СОЦИОЛОГИИ
Как мы уже отмечали, РТИ нельзя считать полностью отвечающей потребностям социологии. В ней отсутствуют многие элементы, без которых невозможно создание теории социологического измерения. Это связано, по большому счету, с тем, что предметом ее изучения не являются ЭС. Ее утверждения исходят из того, что ЭС задана. А ведь для социолога определение вида ЭС — один из самых сложных вопросов. Кроме того, социологические ЭС далеко не всегда имеют свойства, хотя бы отдаленно похожие на свойства чисел. В данной главе мы подробнее рассмотрим, что может дать социологу РТИ. Прежде всего покажем, какова та полезная роль, которую может сыграть рассматриваемый формализм в социологическом исследовании, и чего в этом формализме социологу заведомо не хватает.
14.1. Основные задачи, решаемые РТИ
Начнем с перечисления тех полезных для социолога результатов, которые содержатся в РТИ. Эти результаты сводятся к возможности решения следующих задач.
1. Доказательство существования шкал.
РТИ содержит много результатов, имеющих примерно такую формулировку: если ЭС обладает такими-то свойствами (при этом она может быть определена и не в виде ЭСО; в качестве "свойств" может выступать, например, требование адекватности одной из рассмотренных выше моделей восприятия), то ее можно гомоморфно отобразить в ЧСО. Подобные утверждения, несомненно, могут быть весьма полезны. Другое дело, что упомянутое "если" может быть весьма проблематичным для социолога.
2. Определение степени единственности шкалы.
Обосновав возможность построения шкалы в рамках РТИ, обыч-
но показывают, с какой точностью определены получившиеся
шкальные значения. По существу это сводится к доказательству того, что получившаяся шкала является шкалой такого-то типа.
Подчеркнем, что именно в рамках РТИ было доказано, что с помощью ряда конкретных методов шкалирования получаются шкалы определенного типа. Это касается, например, многих методов парных сравнений, в частности тех, которые были рассмотрены в п. 6.
3. Проблема адекватности математического метода и ее решение в теории измерений.
Проблема адекватности является центральной для РТИ. Описанное выше стремление ученых к выработке четких представлений о том, что есть измерение в гуманитарных науках, было направлено в основном на решение вполне практической задачи — понять,