ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ООО «Инфоурок»
Контрольное задание по дисциплине:
«Информатика»
На тему:
«ЕГЭ по информатике для 11 класса»
Исполнитель:
Фролова Л.В
Часть 1
Задание 1.
На рисунке справа схема дорог Н-ского района изображена в виде графа; в
таблице слева содержатся сведения о протяжённости каждой из этих дорог
(в километрах).
| | П1 | П2 | П3 | П4 | П5 | П6 | П7 |
| П1 | + | 20 | | 15 | 10 | 8 | 9 |
| П2 | 20 | + | | 11 | | 25 | |
| П3 | | | + | | 5 | | |
| П4 | 15 | 11 | | + | | | |
| П5 | 10 | | 5 | | + | 7 | 6 |
| П6 | 8 | 25 | | | 7 | + | |
| П7 | 9 | | | | 6 | | + |
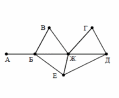
Так как таблицу и схему рисовали независимо друг от друга, то нумерация
населённых пунктов в таблице никак не связана с буквенными
обозначениями на графе. Определите, какова протяжённость дороги из
пункта Д в пункт Е. В ответе запишите целое число — так, как оно указано
в таблице.
Ответ: __________________________.
Задание 2.
Логическая функция F задаётся выражением (¬???? /\ ¬???? ) \/ (???? ≡ z ) \/ w.
На рисунке приведён частично заполненный фрагмент таблицы истинности
функции F, содержащий неповторяющиеся строки. Определите, какому
столбцу таблицы истинности функции F соответствует каждая из
переменных x, y, z, w.
| ? | ? | ? | ? | F |
| | 0 | 0 | 1 | 0 |
| 1 | | 1 | | 0 |
| 1 | 0 | | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут
соответствующие им столбцы. Буквы в ответе пишите подряд, никаких
разделителей между буквами ставить не нужно.
Ответ: __________________________.
Задание 3.
Ниже представлены две таблицы из базы данных. Каждая строка таблицы 2
содержит информацию о ребёнке и об одном из его родителей. Информация
представлена значением поля ID в соответствующей строке таблицы 1.
Определите на основании приведённых данных количество братьев и сестёр
Гуревича И.И.
Таблица 1.
| ID | Фамилия И.О | Пол |
| 85 | Петров В.В | М |
| 95 | Вельберг И.В | М |
| 42 | Фертих С.Ф | Ж |
| 71 | Гоммер Л.В | Ж |
| 23 | Ломоносов Н.П | М |
| 13 | Черныш А.Н | М |
| 82 | Шарипова А.А | Ж |
| 10 | Гайлит П.А | М |
| ID Родителя | ID Ребенка |
| 13 | 95 |
| 95 | 23 |
| 71 | 10 |
| 95 | 42 |
| 10 | 82 |
| 71 | 42 |
| 71 | 23 |
| 95 | 10 |
| 85 | 95 |
Ответ: __________________________.
Задание 4.
По каналу связи передаются сообщения, содержащие только четыре буквы:
А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий
условию Фано. Для букв А, Б, В используются такие кодовые слова: А – 0; Б
– 111; В – 100.
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет
допускать однозначное декодирование. Если таких кодов несколько,
укажите код с наибольшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является
началом другого кодового слова. Это обеспечивает возможность
однозначной расшифровки закодированных сообщений.
Ответ: __________________________.
Задание 5.
На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему
новое число R следующим образом.
1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по
следующему правилу: если N чётное, в конец числа (справа)
дописывается сначала ноль, а затем единица. В противном случае,
если N нечётное, справа дописывается сначала единица, а затем
ноль.
Например, двоичная запись 100 числа 4 будет преобразована в 10001, а
двоичная запись 111 числа 7 будет преобразована в 11110.
Полученная таким образом запись (в ней на два разряда больше, чем в записи
исходного числа N) является двоичной записью числа R – результата работы
данного алгоритма.
Укажите максимальное число R, которое меньше 125 и может являться
результатом работы данного алгоритма. В ответе это число запишите в
десятичной системе счисления.
Ответ: __________________________.
Задание 6.
Запишите число, которое будет напечатано в результате выполнения
следующей программы. Определите, при каком наименьшем введённом
значении переменной s программа выведет число 81. Для Вашего удобства
программа представлена на четырёх языках программирования.
| C++ | Паскаль |
| #include using namespace std; int main() { int s, n; cin >> s; n = 1; while (s < 60) { s = s + 5; n = n * 3; } cout << n << endl; return 0; } | var s, n: integer; begin readln (s); n := 1; while s < 60 do begin s := s + 5; n := n * 3 end; writeln(n) end. |
| Python | Алгоритмический язык |
| s = int(input()) n = 1 while s < 60: s = s + 5 n = n * 3 print(n) | алг нач цел n, s ввод s n := 1 нц пока s < 60 s := s + 5 n := n * 3 кц вывод n кон |
Ответ: __________________________.
Задание 7.
Производилась двухканальная (стерео) звукозапись с частотой
дискретизации 256 кГц и 16-битным разрешением. В результате был
получен файл размером 200 Мбайт, сжатие данных не производилось.
Определите приблизительно, сколько времени (в минутах) производилась
запись. В качестве ответа укажите ближайшее к времени записи целое число,
кратное 5.
Ответ: __________________________.
Задание 8.
Вася составляет трехбуквенные слова, в которых встречаются только буквы
З, И, К, Л, М, Н, причём буква З появляется ровно 1 раз. Каждая из других
допустимых букв может встречаться в слове любое количество раз или не
встречаться совсем. Словом, считается любая допустимая
последовательность букв, не обязательно осмысленная. Сколько существует
таких слов, которые может написать Вася?
Ответ: __________________________.
Задания 9–10 выполняются с использованием прилагаемых файлов.
Задание 9.
Откройте файл электронной таблицы, содержащей вещественные числа –
результаты ежечасного измерения температуры воздуха на протяжении трёх
месяцев. Найдите разность между средним арифметическим значением
температуры и ее минимальным значением.
В ответе запишите только целую часть получившегося числа.
Ответ: __________________________.
Задание 10.
С помощью текстового редактора определите, сколько раз, не считая сносок,
встречается слово «лет» в тексте романа в стихах А.С. Пушкина «Евгений
Онегин». Другой формы слова «лет», такие как «Лет» и т.д., учитывать не
следует. В ответе укажите только число
Ответ: ___________________________.
Задание 11.
Для регистрации на сайте некоторой страны пользователю требуется
придумать пароль. Длина пароля – ровно 6 символов. В качестве символов
могут быть использованы десятичные цифры и 27 различных букв местного
алфавита, причём все буквы используются в двух начертаниях: как
строчные, так и прописные (регистр буквы имеет значение).
Под хранение каждого такого пароля на компьютере отводится одинаковое
и минимально возможное целое количество байтов. При этом используется
посимвольное кодирование, и все символы кодируются одинаковым
и минимально возможным количеством битов.
Определите объём памяти в байтах, который используется для хранения
55 паролей.
Ответ: ___________________________.
Задание 12.
Исполнитель Редактор получает на вход строку цифр и преобразовывает её.
Редактор может выполнять две команды, в обеих командах v и w обозначают
цепочки цифр.
заменить (v, w)
нашлось (v)
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (333) ИЛИ нашлось (999)
ЕСЛИ нашлось (333)
ТО заменить (333, 9)
ИНАЧЕ заменить (999, 3)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой ниже
программы к строке, состоящей из 125 идущих подряд цифр 3? В ответе
запишите полученную строку.
Ответ: __________________________.
Задание 13.
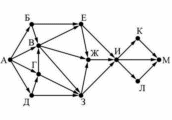
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е,
Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном
направлении, указанном стрелкой.
Сколько существует различных путей из города А в город М, проходящих
через город Л?
Ответ: __________________________.
Задание 14.
Сколько значащих нулей в пятеричной записи следующего выражения?
125+
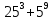
Ответ: __________________________.
Задание 15.
Для какого наименьшего целого числа А формула
((x9) (xx<A) ) ( (yy) (y<12))
тождественно истинна (то есть принимает значение 1 при любых целых
неотрицательных значениях переменных x и y)?
Ответ: __________________________.
Задание 16.
Алгоритм вычисления значения функции F(n), где n – натуральное число,
задан следующими соотношениями:
F(n) = n + 1 при n 2;
F(n) = F(n – 1) + 2×F(n – 2), если n > 2.
Чему равно значение функция F(4)?
Ответ: __________________________.
Задание 17.
Рассматривается множество целых чисел, принадлежащих числовому
отрезку [256; 2566], которые делятся на 7 и не делятся на 21, 23, 31.
Найдите сумму таких чисел и максимальное из них.
В ответе запишите два целых числа: сначала сумму, затем максимальное
число.
Для выполнения этого задания можно написать программу или
воспользоваться редактором электронных таблиц.
Ответ: __________________________.
Задание выполняется с использованием прилагаемых файлов.
Задание 18.
Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может
перемещаться по клеткам, выполняя за одно перемещение одну из двух
команд: вправо или вниз. По команде вправо Робот перемещается в
соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При
попытке выхода за границу квадрата Робот разрушается. Перед каждым
запуском Робота в каждой клетке квадрата лежит монета достоинством
от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также
относится к начальной и конечной клетке маршрута Робота.
Определите максимальную и минимальную денежную сумму, которую
может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.
В ответе укажите одно число – разность максимальной и минимальной сумм.
Исходные данные представляют собой электронную таблицу размером N×N,
каждая ячейка которой соответствует клетке квадрата.
Пример входных данных:
| 1 | 8 | 8 | 4 |
| 10 | 1 | 1 | 3 |
| 1 | 3 | 12 | 2 |
| 2 | 3 | 5 | 6 |
Для указанных входных данных ответом должен быть чисел 19.
Ответ: __________________________.
Задание 19.
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат
две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один
ход игрок может добавить в одну из куч (по своему выбору) один камень
или увеличить количество камней в куче в два раза. Например, пусть в
одной куче 10 камней, а в другой 5 камней; такую позицию в игре будем
обозначать (10, 5). Тогда за один ход можно получить любую из четырёх
позиций: (11, 5), (20, 5), (10, 6), (10, 10). Для того чтобы делать ходы, у
каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах
становится не менее 63. Победителем считается игрок, сделавший
последний ход, т.е. первым получивший такую позицию, при которой в
кучах будет 63 или больше камней.
В начальный момент в первой куче было пять камней, во второй куче –
S камней; 1 ≤ S ≤ 57.
Будем говорить, что игрок имеет выигрышную стратегию, если он может
выиграть при любых ходах противника. Описать стратегию игрока – значит
описать, какой ход он должен сделать в любой ситуации, которая ему может
встретиться при различной игре противника. В описание выигрышной
стратегии не следует включать ходы играющего по этой стратегии игрока,
не являющиеся для него безусловно выигрышными, т.е. не являющиеся
выигрышными независимо от игры противника.
Известно, что Ваня выиграл своим первым ходом после неудачного первого
хода Пети. Укажите минимальное значение S, когда такая ситуация
возможна.
Ответ: __________________________.
Задание 20.
Для игры, описанной в предыдущем задании, найдите два таких значения S,
при которых у Пети есть выигрышная стратегия, причём одновременно
выполняются два условия:
Петя не может выиграть за один ход;
Петя может выиграть своим вторым ходом независимо от того, как
будет ходить Ваня.
Найденные значения запишите в ответе в порядке возрастания.
Ответ: __________________________.
Задание 21.
Два игры, описанной в задании 19, найдите минимальное значение S, при
котором одновременно выполняются два условия:
у Вани есть выигрышная стратегия, позволяющая ему выиграть
первым или вторым ходом при любой игре Пети;
у Вани нет стратегии, которая позволит ему гарантированно выиграть
первым ходом.
Ответ: __________________________.
Задание 22.
Укажите наименьшее натуральное число, при вводе которого эта программа
напечатает сначала 3, потом – 12.
| Python | Паскаль |
| x = int(input()) a, b = 0, 1 while x > 0: a = a + 1 b = b * (x % 10) x = x // 10 print(a); print(b); | var x, a, b: longint; begin readln(x); a := 0; b := 1; while x > 0 do begin a := a + 1 b := b * (x mod 10); x := x div 10; end; writeln(a); write(b); end. |
| Алгоритмический язык | C++ |
| алг начало цел x, a, b ввод x a := 0 b := 0 нц пока х > 0 a := a + 1 b := b* mod(x, 10) x := div(x, 10) кц вывод a, нс, b кон | #include using namespace std; int main(){ int x, a, b; cin>> x; a = 0 ; b = 1; while(x > 0){ a = a + 1; b = b*(x % 10) x = x /10; } cout<< a < |
Ответ: __________________________.
Задание 23.
У исполнителя Утроитель две команды, которым присвоены номера:
1. прибавь 1,
2. умножь на 3.
Первая из них увеличивает число на экране на 1, вторая утраивает его.
Программа для Утроителя – это последовательность команд.
Сколько есть программ, которые число 3 преобразуют в число 36?
Ответ: __________________________.
Задание выполняется с использованием прилагаемых файлов.
Задание 24.
Текстовый файл состоит не более чем из 106 символов X, Y и Z.
Определите максимальное количество подряд идущих одинаковых
символов.
Для выполнения этого задания следует написать программу.
Ответ: __________________________.
Задание 25.
Напишите программу, которая ищет среди целых чисел, принадлежащих
числовому отрезку [1024; 289212], простые числа, то есть числа, имеющие
ровно два натуральных делителя: единицу и само число. Запишите в ответе
сумму всех найденных простых чисел.
Например, в диапазоне [3; 9] есть следующие простые числа: 3,5,7.
Поэтому для этого диапазона ответом является 3+5+7=15.
Ответ: __________________________.
Задание выполняется с использованием прилагаемых файлов.
Задание 26.
Системный администратор раз в неделю создаёт архив пользовательских
файлов. Однако объём диска, куда он помещает архив, может быть меньше,
чем суммарный объём архивируемых файлов.
Администратор хочет сэкономить место на диске для хранения архивов. Изза этого он выбирает 4 наибольших по объему архивов и удаляет их. Тем
самым сэкономив место на диске.
Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей, определите
сэкономленное администратором место.
Входные данные.
В первой строке входного файла находится число N – количество
пользователей (натуральное число большее 4, не превышающее
1000000). В следующих N строках находятся значения объёмов файлов
каждого пользователя (все числа натуральные, не превышающие 100),
каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи
файлы могут быть помещены в архив, затем максимальный размер
имеющегося файла, который может быть сохранён в архиве, при условии,
что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
5
80
30
50
40
34
При таких исходных данных можно сэкономить на файлах объемами 80, 50,
40, 34. Поэтому ответ для приведённого примера 204:
Ответ: __________________________.
Задание выполняется с использованием прилагаемых файлов.
Задание 27.
Имеется набор данных, состоящих из пар положительных целых чисел.
Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма
всех выбранных чисел не делилась на 6 и при этом была минимально
возможной. Гарантируется, что искомую сумму получить можно.
Программа должна напечатать одно число – минимально возможную сумму,
соответствующую условиям задачи.
Входные данные.
Даны два входных файла (файл A и файл B), каждый из которых содержит
в первой строке количество пар N (1 ≤ N ≤ 100000). Каждая из следующих
N строк содержит два натуральных числа, не превышающих 10 000.
Пример организации исходных данных во входном файле:
6
13
512
69
54
33
11
Для указанных входных данных значением искомой суммы должно быть число 20.
Предупреждение: для обработки файла В не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Ответ:______________________________________