Где 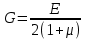- модуль сдвига второго рода

Если решить данную систему относительно напряжений, то получим:

10. 
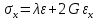
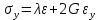
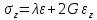
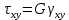
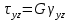
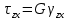
    Постановка задачи теории упругости, прямая и обратная задача.
    

В зависимости от вида граничных условий различают 3 типа граничных задач теории упругости:

1. 
   Когда даны: массовые и поверхностные силы; необходимо найти: компоненты тензора напряжения внутри, компоненты вектора перемещения внутри и на поверхности; все должно соответствовать: дифференциальному уравнению равновесия, закону Гука, краевым условиям
   
2. 
   Когда даны: массовые силы и перемещения на поверхности тела; необходимо найти: перемещение точки внутри тела, компоненты тензора напряжений; все должно соответствовать: закону Гука и дифференциальному уравнению.
   
3. 
   Когда даны: поверхностные силы на одной части поверхности, перемещения на другой части поверхности, массовые силы; необходимо найти: тензор напряжения и перемещения; все должно соответствовать: дифференциальному уравнению, закону Гука, при выполнении смешанных граничных условий.
   

Прямая задача состоит в решении одной из трех основных задач. Определяются напряжения и перемещения точек тела как функции координат, определяющих напряжения деформированного состояния тела в зависимости от внешнего воздействия.

Обратная задача состоит в том, чтобы задавшись либо перемещением либо напряжением определить из основных перемещений или граничных условий все остальные функции.

11. 
    Способы и методы решения задачи теории упругости (уравнения).
    

Решение задачи теории упругости в перемещениях: В дифференциальные уравнения равновесия

---

III подставляется выражение для напряжений VIII и заменяя компоненты деформации по формулам Коши определяется деференциальное уравнение движения твердого тела.







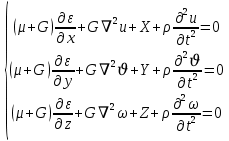
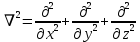
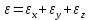
Решение задачи теории упругости в напряжениях: Подставляя компоненты деформации в виде закона Гука VII в условие неразрывности VI с помощью дифференциальных уравнений равновесия III, получим:





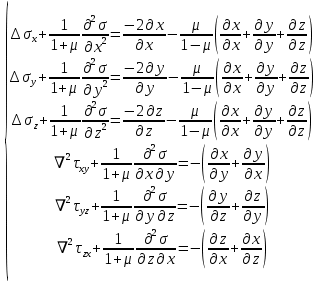
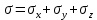
При отсутствии объемных сил, правые части уравнений обращаются в нуль. Используя данное свойство с дифференциальными уравнениями равновесия III и краевыми условиями для напряжений IV, можно определить напряжения.

12. 
    Условная диаграмма растяжения и сжатия, теорема о разгрузке. Эффект Баушингера. Интенсивность напряжений и деформаций.
    

Построение диаграммы выполняется в координатах ;



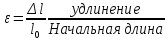
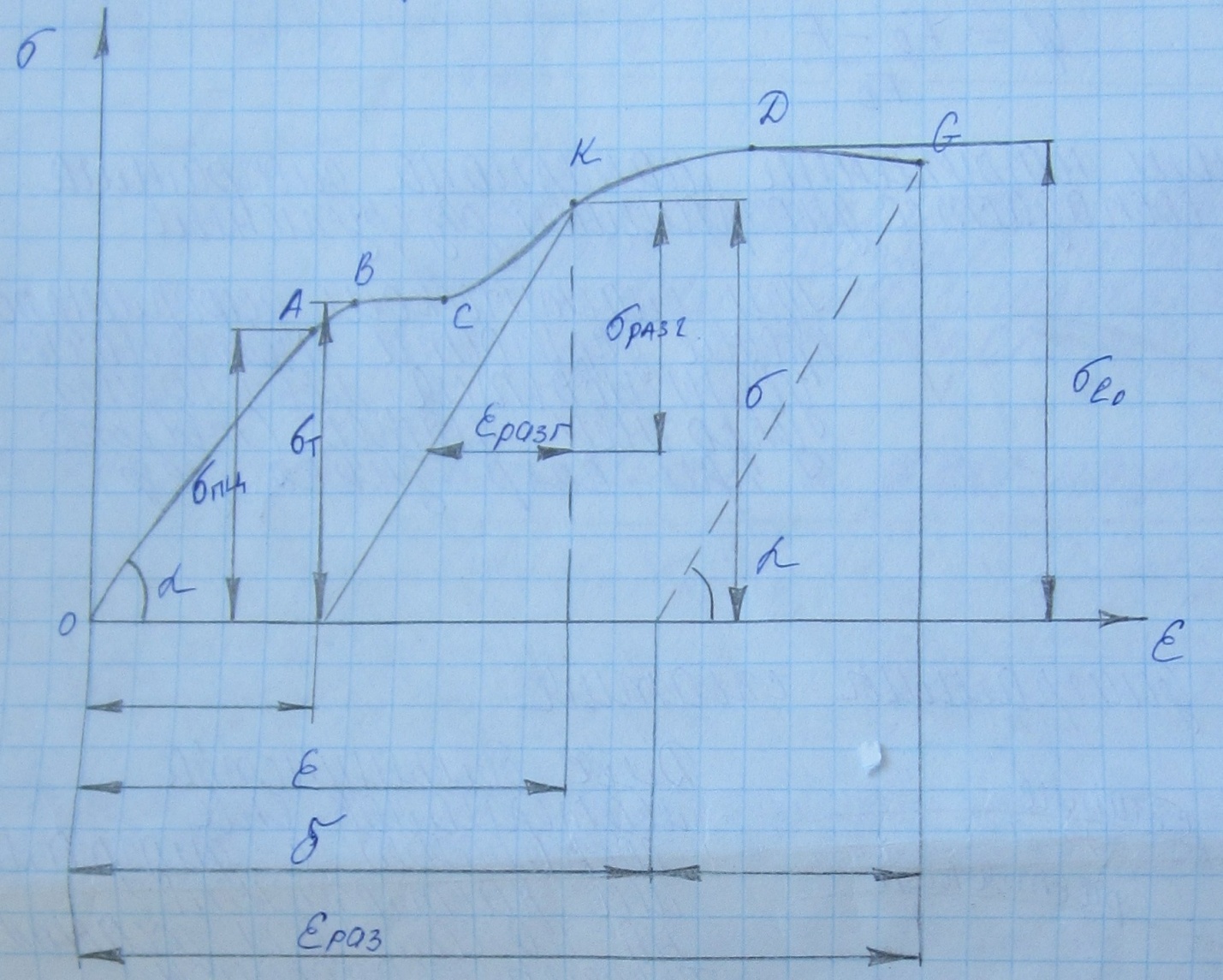
ОА – линейный участок, действует закон Гука

ВС – площадка текучести, деформация при постоянном напряжении

СG – участок упрочнения

---

Теорема о разгрузке

Если образец растянуть до 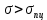(точка К), а затем разгрузить, то диаграмма разгрузки КМ не совпадает с диаграммой первичного нагружения. Это будет прямая параллельная отрезку ОА

Теорема

Уменьшение напряжения при разгрузке 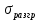пропорционально удлинению деформации 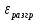. Коэффициент пропорциональности такой же как и в начальной стадии нагружения.

Полное напряжение для деформации 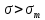есть сама упругих и пластичных деформаци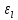й . И .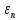

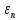– сохраняется после снятия нагрузок и называются остаточной деформацией

Остаточную пластичную деформацию в момент разрыва называют остаточным удлинением δ

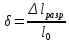чем она больше тем пластичнее материал

Дополнительно выполняются оценка остаточного относительного сужения ψ



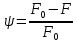
При вторичном нагружении материала диаграмма нагружения совпадает с диаграммой разгружения



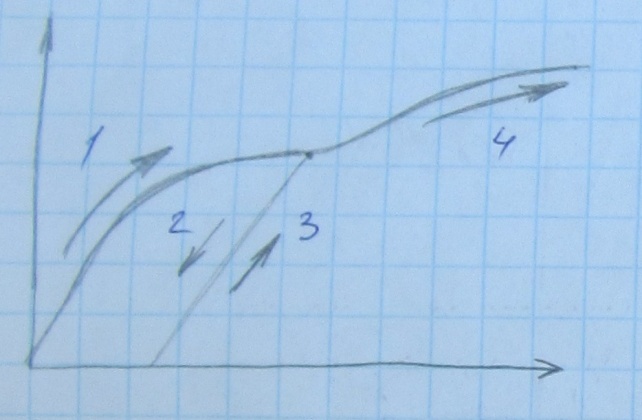
При пластическом деформированным пределом упругости материала увеличивается, происходит упрочнение материала(только при сохранении знака деформации)

Условные диаграммы сжатия



Для большинства материалов они совпадают с диаграммами растяжения на начальном участке. Пределы пропорциональности прочности несколько больше, чем при растяжении.

Данные отличия более существенны для хрупких материалов
Эффект Браушингера. Интенсивность напряжений и деформаций.

---

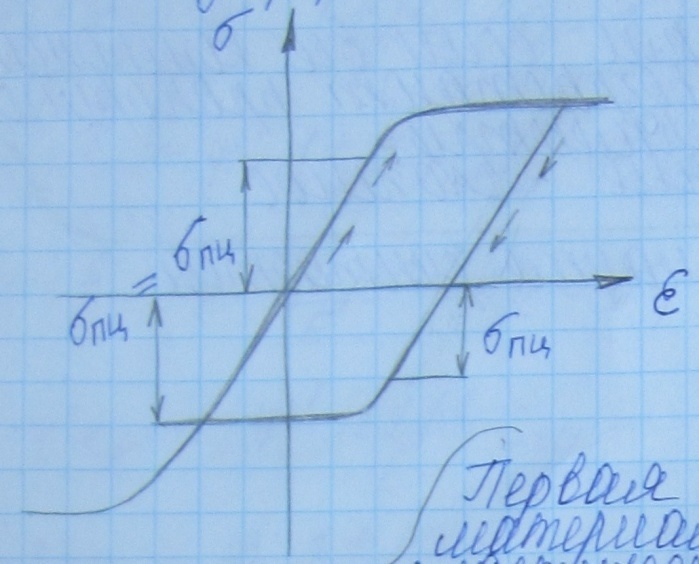
Предел упругости при сжатии пластически деформированного растяжением материала меньше чем недеформированного.

Первая пластическая деформация материала снижает его сопротивления пластическому деформированию, при повторном нагружении противоположные знаки (Эффект Браушингера)

Интенсивность напржений и деформаций



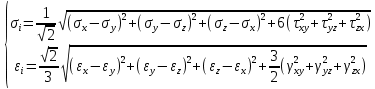
Позволяет управлять закономерностью между сложным напряженым состоянием и простым растяжением

Эффект Баушингера – снижение пределов пропорциональности упругости и текучести материалов в результате изменения знака нагружения, если первоначальная нагрузка вызвала наличие пластической деформации.

Металл подвергнутый слабой пластической деформации нагрузкой одного знака, обнаруживает при перемене знака нагружения пониженное сопротивление пластическим деформациям.

Эффект связывают с наличием остаточных напряжений в наиболее деформированных зернах металла, которые складываясь с рабочими напряжениями при изменении знака нагрузки, вызывают понижение указанных характеристик ( )

13. 
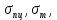
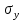    Простое и сложное нагружение, Основные уравнения теории пластичности. Постановка задачи теории пластичности.
    

Нагружения называют простым, если все компоненты тензора напряжения возрастают пропорционально одному общему параметру

В ином случае нагружение – сложное

1 допущение: Объемная деформация считается упругой







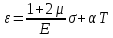
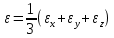
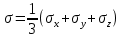
2 допущение: Тензор-девиатор деформации пропорционален тензору-девиатору напряжений

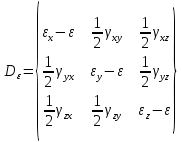тензор напряжений в котором главная диагональ равна 0

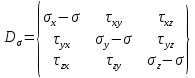условная пропорциональность

---

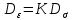
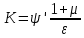
Девиатор направления характеризует отклонение напряженного состояния от состояния всестороннем растяжения-сжатия такие отклонения называются деформацией сдвига и связанные с ними пластические деформации

Из условия пропорциональности выводим уравнение Генки-Илюшина



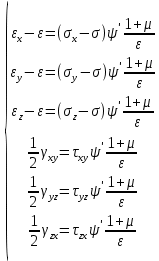
Постановка задачи теории пластичности

Для тела, находящегося под воздействием массовых сил и поверхностных нагрузок необходимо определить неизвестные перемещения, напряжения и деформации

Для решения задач теории пластичности используют уравнения теории равновесия:



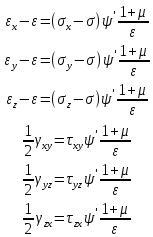
Краевые условия:







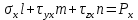
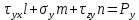
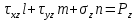
Уравнения Коши:







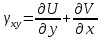
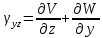
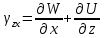
Уравнения неразрывности (сплошности) деформаций

14. 
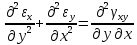
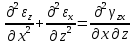
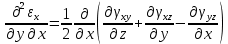
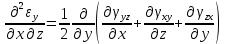
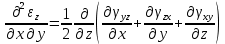
    Теорема Ильюшина о простом нагружении. Метод переменных параметров.
    

Напряжения и деформации как функции свойств материала определяются уравнением

??????????

Задача теории пластичности является нелинейной. Наличие условия единственности решения данной задачи доказано Ильюшиным.

---

Смотрите также файлы

• Введение (Задачи организации работы складского хозяйства строительной организации).docx

• Инструкция по просмотру результатов и подаче апелляций.docx

• Вопрос 1 Регулярно ли Вы питаетесь в ресторане быстрого обслуживания да, нет.docx

• Курсовой проект пм 01 Участие в проектировании зданий и сооружений мдк 01. 02 Проект производства работ Тема Проектирование проекта производства работ на возведение жилого дома с декоративной штукатуркой Курсовой проект выполнен.docx

• 1. Д. Исабековті пке драмасында суреттелген отбасылы мселе.docx