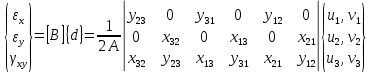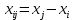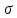. Их величина пропорциональна корню 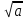из размера трещины и стремится к бесконечности вершины трещины при 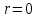. При больших , .

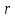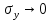Данная особенность есть следствие а) упругого решения (бесконечность напряжений); б) использование первых членов рядов 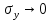на большом расстоянии от вершины трещины.

В уравнениях описывающих напряженное состояние функции 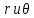имеют простой вид. В обобщенном виде эти уравнения можно записать: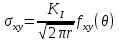





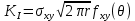
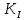- коэффициент интенсивности напряжений. Функция позволяющая определить и описать напряженное деформированное состояние при вершине трещины.

19. 
    Критерии роста трещины. Уравнение Периса. Прогноз ресурса детали с трещиной.
    

Критерий начала распространения трещин является основой механики разрушения, т.к. не может быть получен из теории упругости или пластичности.

1. 
   Энергетический критерий (Гриффитса)
   

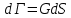
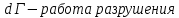
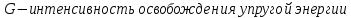
Для увеличения размера трещины на некоторый размер 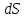с увеличением площади поверхности трещины требуется израсходовать энергию равную по величине работе, которую надо затратить, чтобы обеспечить целостность материала перед трещиной. Эта работа с обратным знаком есть работа разрушения. Образование новых участков поверхности трещины, свободных от нагрузок приведет к деформированию части тела, что будет сопровождаться выделением накопленной в теле упругой энергии.

Было установлено, что

---

работа разрушения, есть работа пластической деформации материала в вершине трещины.

2. 
   Силовой критерий Ирвина
   

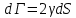
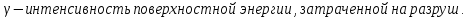
Предполагая, что зона пластических деформаций в вершине трещины мала по сравнению с размером трещины, высвобождение упругой энергии определяется только деформациями тела, а затраты энергии на разрушение идут на пластические деформации материала.

В случае если граница тела при увеличении трещины остается неподвижна, то работа внешних сил=0 и непосредственно получится выражение:



Если на границах тела действуют постоянные силы, то правая часть уравнения


есть разница между работой внешних сил и энергией деформации. Эта разность равна G. Для определения потока энергии в вершине трещины мысленно введем разрез на поверхностях которого действуют силы, противоположные силам пытающимся раскрыть трещину. При раскрытии разреза на 1 единицу площади работа сил 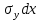на перемещение 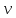дает поток энергии: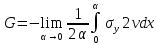



Подставляя в данное выражение асимптотические зависимости для 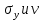в вершине трещины получим что: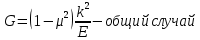





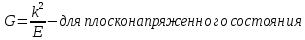
Трещина распространяется при условии если:

1. 
   Интенсивность высвобождения энергии G достигает критической величины:
   

2. 
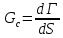
   Коэффициент интенсивности напряжения достинает критической величины
   

---

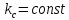
Уравнение Периса.

Кинетическая диаграмма усталостных трещин







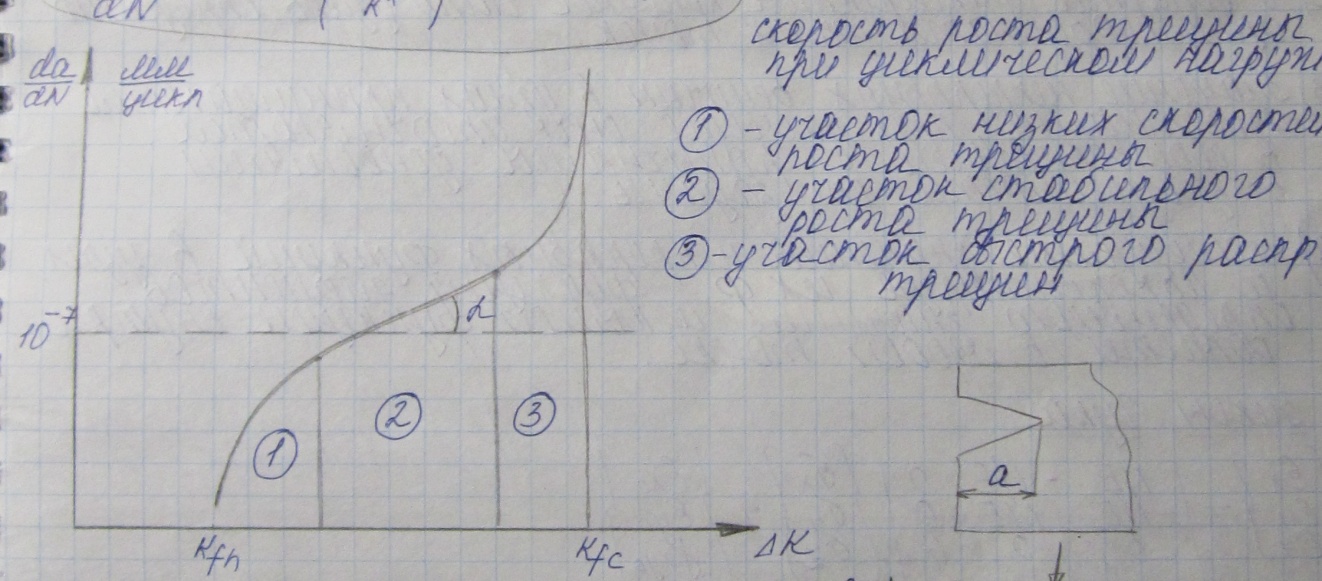
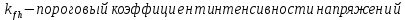
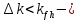трещины не развиваются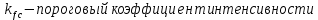



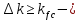трещины распространяются со скоростью звука

2 участок Перис предложил описать степенным уравнением:



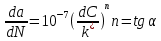
Прогноз ресурса детали с трещиной.

Исходными данными для анализа являются действующие напряжения, характеристики трещиностойкости материала 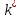, , 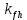, 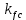n и начальный размер трещин.

По действующим напряжениям определяют 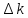: если при всех условиях нагружения 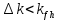- тещина не развивается; если 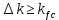- деталь эксплуатироваться не может; если 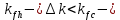трещина развивается, необходимо определить ресурс детали до поломки. Для этого используют уравнение Периса: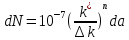

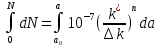
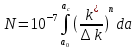
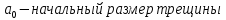
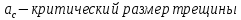
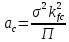
20. 
    Основы метода конечных элементов, этапы решения, матричная форма записи уравнений теории упругости. Функции формы конечного элемента.
    

---

Сущность метода. Любую напрерывную функцию можно апроксимировать моделью, состоящую из отдельных элементов или участков. На каждом из элементов исследуемая величина апроксимируется кусочно-непрерывной функцией, которая строится в конечном числе точек элемента. В общем случае непрерывная величина считается неизвестной, необходимо определить ее значение во внутренних точках области.

Этапы решения.

1) область разбивается на конечное число подобластей, называемых элементами. Они имеют общие узловые точки и в совокупности апроксимируют форму области.

2) В области фиксируется конечное число узлов, часть из них общие. Определяются координаты этих точек.

3) Значение непрерывной величины в узлах принимается известным, при расчете они уточняются в соответствии с наложенными граничными условиями в зависимости от задачи.

4) Используя значения функции в узлах, определяют значение функции в любой точке.

Матричная форма записи уравнений теории упругости.

Перемещение:

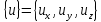
Закон Гука:



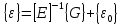
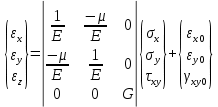
Начальная деформация:



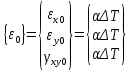
Уравнения Коши:



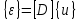
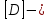матрица деференцирования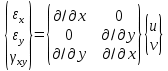



Функции формы конечного элемента.

Рассмотрим стержневой элемент длиной 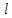, поперечным сечением 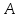и модулем Юнга 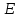. Введем две функции 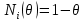, , 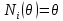где 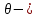относительная координата точки элемента в локальной СК: .

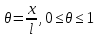Смещение любой точки в пределах элемента

---

.



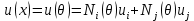
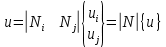
Линейная функция 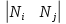называется функцией формы стержневого элемента. Она апроксимирует перемещения в пределах элемента.

21. 
    Матрица жесткости конечного элемента. Разрешающие уравнения метода конечных элементов.
    

Матрица жесткости 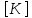связывает между собой узловые усилия и перемещения, включает физические константы материала.

Для стержневого элемента:





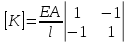
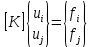
Для балочного элемента:





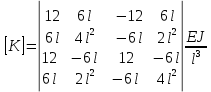
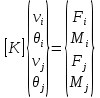
Разрешающие уравнения МКЭ.

Линейный плоский треугольный элемент. Позволяет апроксимировать геометрические области любой формы. Каждый узел имеет две степени свободы. Смещение 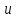и в любой точке внутри элемента является линейными функциями координат этой точки.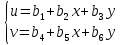



Деформации в пределах элемента являются постоянными:







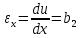
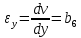
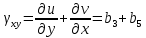
Перемещения узловых точек элемента определяется уравнениями:



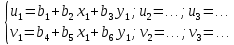
Перемещения точки в пределах элемента через функцию формы:









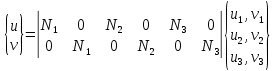
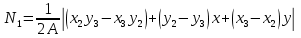
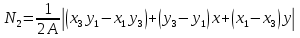
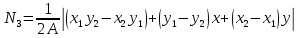
Деформация в точках элемента:

---

Смотрите также файлы

• Введение (Задачи организации работы складского хозяйства строительной организации).docx

• Инструкция по просмотру результатов и подаче апелляций.docx

• Вопрос 1 Регулярно ли Вы питаетесь в ресторане быстрого обслуживания да, нет.docx

• Курсовой проект пм 01 Участие в проектировании зданий и сооружений мдк 01. 02 Проект производства работ Тема Проектирование проекта производства работ на возведение жилого дома с декоративной штукатуркой Курсовой проект выполнен.docx

• 1. Д. Исабековті пке драмасында суреттелген отбасылы мселе.docx