Файл: Тема вкр Формирование функциональной грамотности на уроках математики Рукопись статьи по теме исследования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема ВКР: Формирование функциональной грамотности на уроках математики
Рукопись статьи по теме исследования
Куманькина А. А.
Магистрант МГПУ имени М. Е. Евсевьева
Ключевые слова: функциональная грамотность, математическая грамотность, КИМ, ОГЭ.
Аннотация
В статье рассматривается формирование функциональной грамотности обучающихся на уроках математики в рамках подготовки к основному государственному экзамену по математике. А также представлен пример. Формирование функциональной грамотности на уроках в целом повысит жизненные шансы обучающихся: их востребованность на рынке труда и общего успеха в жизни.
Функциональная грамотность – способность человека вступать в отно- шения с внешней средой и максимально быстро адаптироваться и функцио- нировать в ней. Главным отличием функциональной грамотности от элементарной грамотности это уровень ЗУН (знаний, умений, новыков), который обеспечивает личности в системе социальных отношений нормально функционировать. Этот уровень ЗУН как минумум необходим для осуществления жизнедеятельности.
Функциональная грамотность делится на следующие виды: читательская грамотность, математичсекая грамотность, финансовая грамотность, естественно-научная грамотность. Под математичсекой грамотностью понимается сочетание математических знаний, умений, опыта и способностей человека, которые успешно можно применить для разрешения разных жизненных проблем, в которых требуется использование математики.
На уроках математики сформировать функциональную грамотность можно с помощью выполнения заданий, в кототрых необходимо сформулировать ситуацию на языке математики, установить связи и интегрировать материал из разных областей математики, выделить в жизненных ситуациях проблему
, решаемую средствами математики, построить модель решения.
В качестве усиления акцента на проверку математических знаний в различных ситуациях произошел ряд изменений в основном государственном экзамене по математики. Главным нововведением в экзамене по математике является добавление блока практико-ориентированных заданий № 1-5, которые связаны одним сюжетом. Помимо этого, уменьшилось количество заданий за счет объединения двух заданий (задание 8, задание 13 в контрольно-измерительных материалов 2020 г.). Было заменено 12 задание (КИМ 2020 г.) на работу с последовательностями и прогрессиями на задание 14 (КИМ 2021 г.) с практическим содержанием, нацеленное на проверку применения знаний о последовательностях и прогрессиях в прикладных ситуациях. В связи с этим уменьшился первичный максимальный балл, который можно набрать на экзамене по математике с 32 на 31. Такие изменения были сделаны для более точного определения полученных обучающимися умений и навыков в рамках сдаваемого предмета.
Пример решения практико-ориентированных задач ОГЭ – 2022г.
Задачи про зонт.
Двум друзьм Егору и Никите стало интересно, как же рассчитать площадь поверхности зонта. Первоначально кажется, что зонт круглый, а его купол напоминает сферический сигмент. Но если присмотреться, то видно, что купол зонтасостоит из десяти отдельных клиньев, натянутых на каркас из десяти спиц (рисунок 1).

Рисунок 6.1 Форма зонта
Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
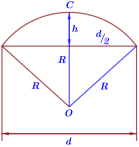
Егору и Никите удалось измерить расстояние между концами соседних спиц а. Оно оказалось равно 32 см. Высота купола зонта h (рисунок 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 110 см.
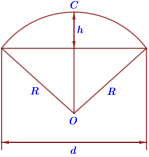
Рисунок 6.2 Чертеж
1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 5,8 см.
Решение:
1) найдем треть длины спицы:
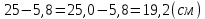
2) найдем длину всей спицы:
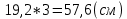
Ответ: 57,6
2. Поскольку зонт сшит из треугольников, рассуждал Максим, площадь его поверхности можно найти как сумму площадей треугольников. Вы- числите площадь поверхности зонта методом Максима, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 57,2 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
Решение:
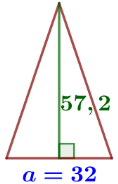
Всего треугольников (клиньев) – 10
Найдем площадь одного треугольника:
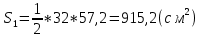
Площадь всего зонта (10 треугольников):
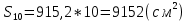 .
.Ответ: 9150
3. Влад предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что OC = R (рис. 2). Ответ дайте в сантиметрах.
Решение:
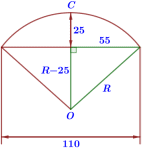
Найдем радиус по теореме Пифагора:
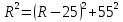
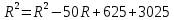
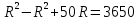
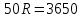
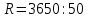
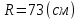
Ответ: 73
4. Влад нашёл площадь купола зонта как площадь поверхности сфери- ческого сегмента по формуле , где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Влада. Чис ло округлите до 3,14. Ответ дайте в квадратных сантиметрах.
Решение:
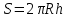
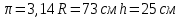
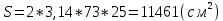
Ответ:
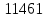
5. Рулон ткани имеет длину 20 м и ширину 140 см. На фабрике из этого рулона были вырезаны треугольные клинья для 26 зонтов, таких же, как зонт, который был у Максима и Влада. Каждый треугольник с учётом припуска на швы имеет площадь 980 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?
Решение:
Общая площадь рулона ткани: рулона
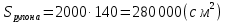 .
.Площадь ткани для одного зонта (10 треугольников):
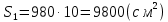 .
.Площадь ткани для 26 зонтов:
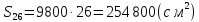 .
.Площадь ткани, ушедшей в обрезки:

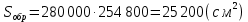 .
.Ткань:
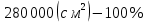
Обрезки:
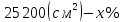
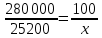
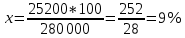
Ответ: 9
Для решения данных заданий у обучающегося должна быть сформирована (на должном уровне) читательская грамотность, а также он должен обладать следующими предметными знаниями:
-
Конвертация величин; -
Составление и решение линейного уравнения; -
Нахождение площади треугольника; -
Нахождение площади поверхности; -
Применение теоремы Пифагора; -
Составление пропорции и нахождение неизвестного члена пропорции; -
Округление чисел.