Файл: Анализ и синтез комбинационных схем.doc

2.2Законы алгебры логики

Свойства функций И, ИЛИ, НЕ называются законами алгебры логики. Приведем некоторые из них, которые потребуются в дальнейшем:

(12)

(13)

(14)

(15)

(16)

(17)

Функционально полная система функций называется минимальной, если удаление из нее хотя бы одной функции делает систему неполной. Базис {И, ИЛИ, НЕ} не является минимальным, так как из него можно исключить либо функцию И, либо функцию ИЛИ с сохранением полноты. Это доказывается тем, что функция И(ИЛИ) может быть выражена через функции ИЛИ(И) и НЕ с помощью формул де Моргана (15) и (16). Взяв отрицание над левой и правой частями формул (15) и (16) и учитывая формулу (12) – закон двойного отрицания, получим:

(18)

(19)

Таким образом, системы {И, НЕ} и {ИЛИ, НЕ} образуют минимальные базисы. Формулы (18) и (19) позволяют переходить от одной формы записи к другой.

К законам алгебры логики относятся также формулы с константами:

(20)

---

(21)

2.3Реализация функций алгебры логики

Понятие базиса играет существенную роль при реализации ФАЛ на логических элементах. Логическим элементом называется элемент, реализующий некоторую логическую функцию. На рис. 3, а, б, в приведены соответственно обозначения логических элементов, реализующих функции И, ИЛИ, НЕ.

а) б) в)

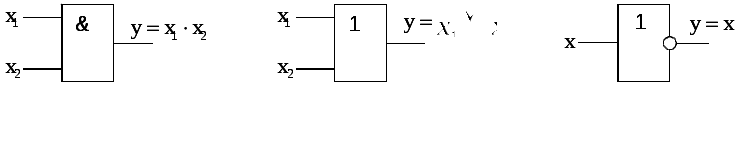
Рис. 3. Логические элементы И, ИЛИ, НЕ
Они могут быть построены на транзисторах, интегральных микросхемах, магнитных кольцах и других элементах. На рис. 4, а, б, в показан пример реализации функций И, ИЛИ, НЕ на релейно-контактных элементах.
а) б) в)



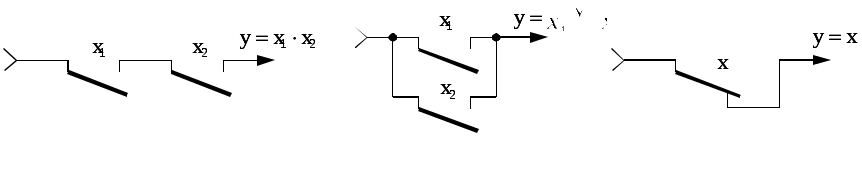
Рис. 4. Реализация функций И, ИЛИ, НЕ на релейно-контактных элементах
Построение схем в базисе {И, ИЛИ, НЕ} производится по следующим правилам.

1. 
   Для реализации каждой логической операции используется соответствующий логический элемент.
   
2. 
   Порядок выполнения операций: НЕ, И, ИЛИ.
   
3. 
   Выражения в скобках и под знаком отрицания реализуются в первую очередь.
   

На рис. 5 приведен пример построения схемы для функции в базисе {И, ИЛИ, НЕ}.

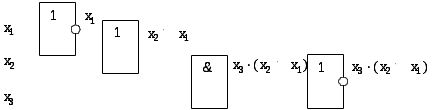
Рис. 5. Реализация ФАЛ в базисе {И, ИЛИ, НЕ}
Построение релейно-контактных схем производится по следующим правилам.

1. 
   Порядок выполнения операций: НЕ, И, ИЛИ.
   
2. 
   Конъюнкция реализуется за счет последовательного соединения контактов (рис. 4, а), дизъюнкция – за счет параллельного (рис. 4, б).
   
3. 
   Переменной без отрицания соответствует фронтовой контакт (рис. 4, а, б), переменной с отрицанием – тыловой (рис. 4, в).
   
4. 
   Выражения в скобках и под знаком отрицания реализуются в первую очередь.
   
5. 
   Если в формуле есть знак отрицания над выражением, то она преобразуется с помощью формул де Моргана (15), (16) до тех пор, пока знак отрицания не останется только над переменными.
   

Альтернативой является применение дополнительного реле.

На рис. 6 приведен пример построения схемы по функции

---

с использованием дополнительного реле.

Рис. 6. Реализация схемы с использованием дополнительного реле



Для реализации ФАЛ, заданной логической формулой, необходимо иметь столько типов логических элементов, сколько функций содержится в базисе, в котором записана ФАЛ.

Реализация ФАЛ возможна также на базе одного логического элемента. Такими элементами являются:

1. 
   элемент И-НЕ (рис. 7, а), реализующий функцию Шеффера;
   
2. 
   элемент ИЛИ-НЕ (рис. 7, б), реализующий функцию Вебба.
   

а) б)


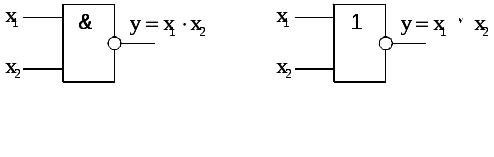
Рис. 7. Реализация функций Шеффера и Вебба на логических элементах
Каждый из этих элементов составляет функционально полную систему алгебры логики. На рис. 8 показана реализация основных ФАЛ на элементе ИЛИ-НЕ. На рис. 9 показана реализация основных ФАЛ на элементе И-НЕ.
а) б)

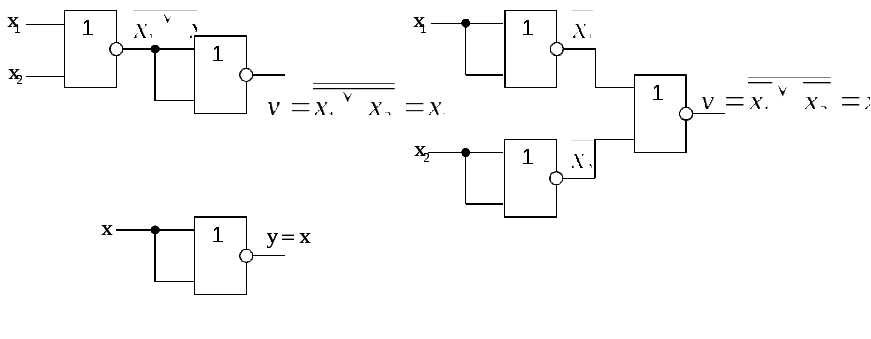
в)

Рис. 8. Реализация функций И, ИЛИ, НЕ с использованием элемента Вебба

а) б)

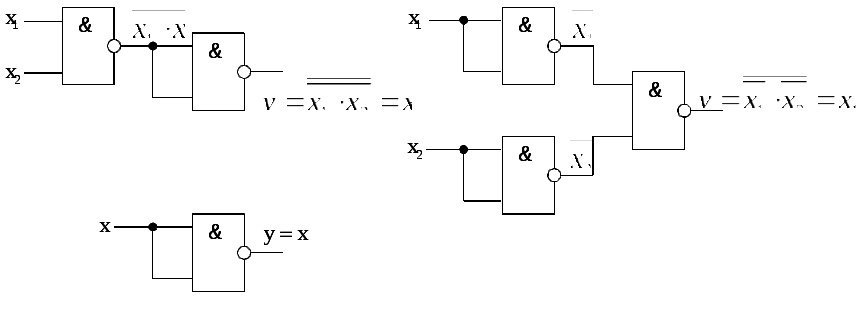
в)


Рис. 9. Реализация функций И, ИЛИ, НЕ с использованием элемента Шеффера

Построение схем в базисах {И-НЕ} и {ИЛИ-НЕ} производится путем замены каждого элемента схемы, реализованной в базисе {И, ИЛИ, НЕ}, на эквивалентный элемент, реализованный в соответствующем базисе (рис. 8, 9).

---

2.4Минимизация ФАЛ с помощью карт Карно

Так как одна и та же ФАЛ может быть записана с помощью различных формул, то возникает задача получения минимальной формы записи (с минимальным числом букв), которая потребует минимальных затрат аппаратуры при реализации.

Рассмотрим процесс минимизации ФАЛ с помощью карт Карно. Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более шести. Карта Карно (рис. 10) является другой формой представления таблицы истинности (табл. 5). Каждая клетка карты соответствует строке таблицы (двоичному набору). Часть клеток (половина), которым соответствует значение x_i= 1, отмечается чертой. Соответственно в областях, не обозначенных чертой, переменная x_i= 0.
Таблица 5

Таблица истинности

№	x1	x2	x3	x4	y
0	0	0	0	0	0
1	0	0	0	1	1
2	0	0	1	0	0
3	0	0	1	1	1
4	0	1	0	0	1
5	0	1	0	1	1
6	0	1	1	0	1
7	0	1	1	1	1
8	1	0	0	0	0
9	1	0	0	1	0
10	1	0	1	0	1
11	1	0	1	1	0
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	1

---

Для задания ФАЛ в карте Карно надо проставить 1 в тех клетках, которые соответствуют разрешенным наборам. В карте на рис. 10 задана ФАЛ из табл. 5.


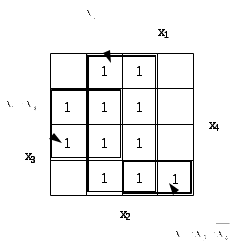
Рис. 10. Карта Карно
Минимизация ФАЛ по карте Карно заключается в объединении соседних клеток в прямоугольные контуры, причем соседними считаются и клетки, разделенные внешней границей карты.
Минимизация производится по следующим правилам.

1. 
   Все единицы должны быть включены в прямоугольные контуры.
   
2. 
   Во всех клетках контура должны стоять единицы.
   
3. 
   Число клеток в контуре должно быть кратным степени числа 2: 1, 2, 4, 8, … .
   
4. 
   Контуры могут накладываться друг на друга.
   
5. 
   Контуры, все клетки которых уже вошли в другие контуры, являются лишними.
   
6. 
   Для получения наиболее простой формулы надо выбирать контуры с максимальным числом клеток.
   
7. 
   Каждому контуру соответствует конъюнкция, составленная из переменных, значения которых не изменяются во всех клетках контура.
   
8. 
   Конъюнкции контуров объединяются знаками дизъюнкции.
   

Ниже представлена ФАЛ, соответствующая карте Карно на рис. 10:



Минимизируем функцию, представленную своими разрешёнными наборами, с использованием карт Карно (рис. 11):

_.

В карте Карно от пяти переменных два контура, удовлетворяющие указанным правилам, объединяются в один контур, если они расположены симметрично относительно центральной оси. Например, контур на рис. 11, соответствующий конъюнкции .


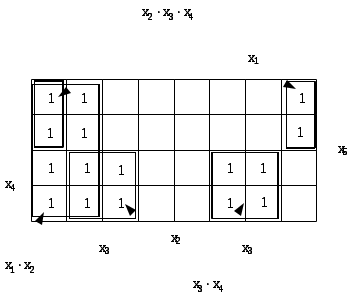
Рис. 11. Минимизация по карте Карно
В итоге мы получаем следующую функцию:

---