ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 190
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1Понятие комбинационной схемы и функции алгебры логики
2.3Реализация функций алгебры логики
2.4Минимизация ФАЛ с помощью карт Карно
4.2Построение релейно-контактной схемы
4.3Построение таблицы истинности
4.5Построение схемы в базисе {И, ИЛИ, НЕ}
4.6Построение схемы в базисе Шеффера {И-НЕ}
4.7Построение схемы в базисе Вебба {ИЛИ-НЕ}
4.8Запись исходной формулы в базисе И, НЕ
4.9Запись исходной формулы в базисе ИЛИ, НЕ
3Методика выполнения работы
-
Ознакомиться с разделом 2 данных методических указаний. -
Получить вариант у преподавателя. -
Для функции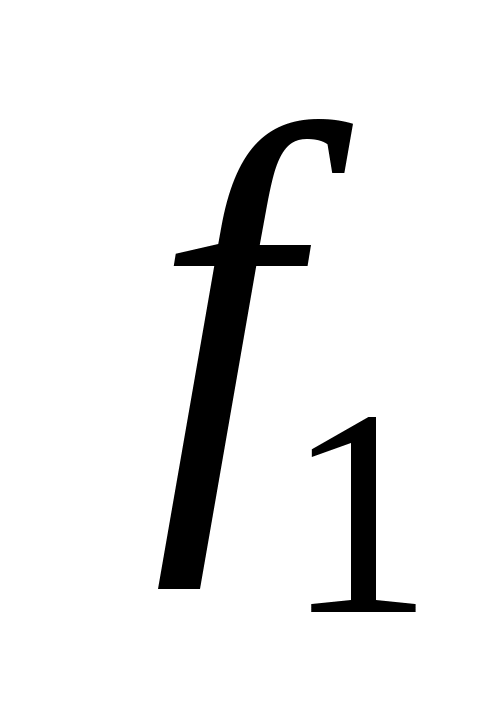 выполнить следующее:
выполнить следующее:
-
построить релейно-контактную схему; -
построить таблицу истинности; -
записать ДСНФ и КСНФ; -
построить схему в базисе {И, ИЛИ, НЕ}; -
построить схему в базисе Шеффера {И-НЕ}; -
построить схему в базисе Вебба {ИЛИ-НЕ}; -
записать исходную формулу в базисе И, НЕ; -
записать исходную формулу в базисе ИЛИ, НЕ.
-
Для функции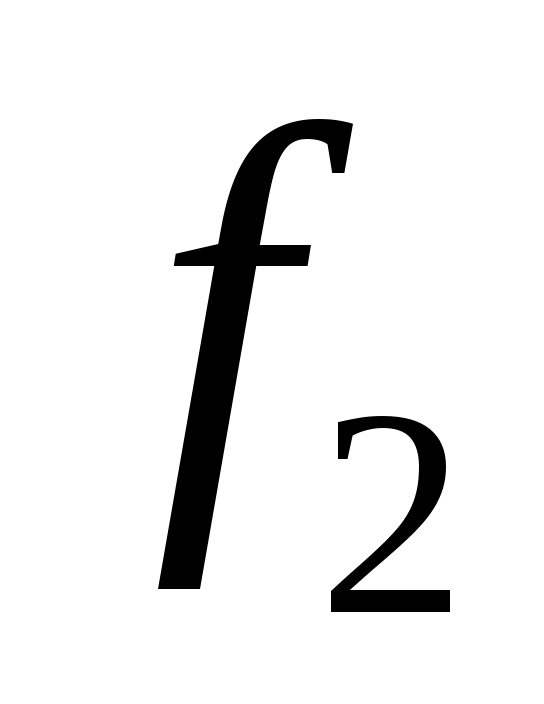 выполнить следующее:
выполнить следующее:
-
осуществить минимизацию по карте Карно; -
записать минимизированную ФАЛ.
4Пример выполнения работы
4.1Исходные данные
4.2Построение релейно-контактной схемы
Исходя из правил построения релейно-контактных схем, функцию f1 необходимо преобразовать, исключив знаки отрицания над выражением (используем формулы де Моргана (15) и (16)):
Релейно-контактная схема представлена на рис. 12.
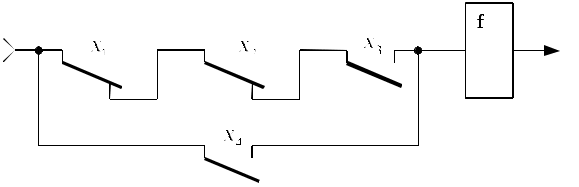
Рис. 12. Релейно-контактная схема
Применим дополнительное реле для построения схемы (рис. 13).
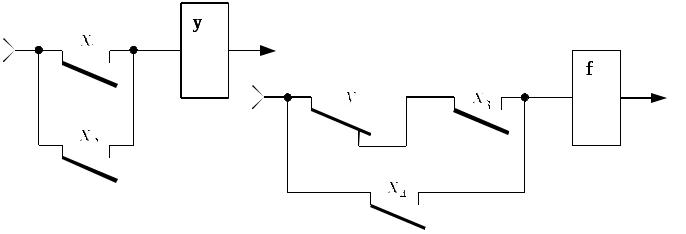
Рис. 13. Релейно-контактная схема
с использованием дополнительного реле
4.3Построение таблицы истинности
Построение таблицы удобно проводить поэтапно, выделяя столбец для отдельных выражений исходной формулы (табл. 6).
Таблица 6
Таблица истинности
| № | x1 | x2 | x3 | x4 | | | | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 12 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
4.4ДСНФ и КСНФ
ДСНФ исходной функции:
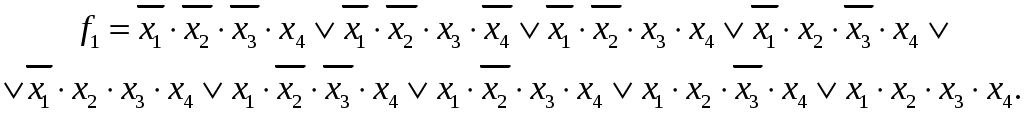
КСНФ исходной функции:
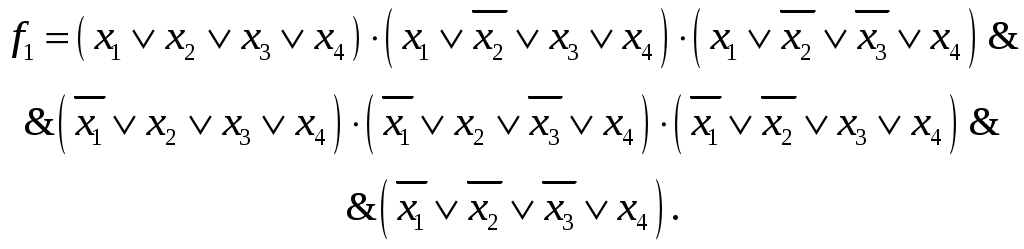
4.5Построение схемы в базисе {И, ИЛИ, НЕ}
Схема, реализующая функцию
Рис. 14. Реализация функции
4.6Построение схемы в базисе Шеффера {И-НЕ}
Схема, реализующая функцию
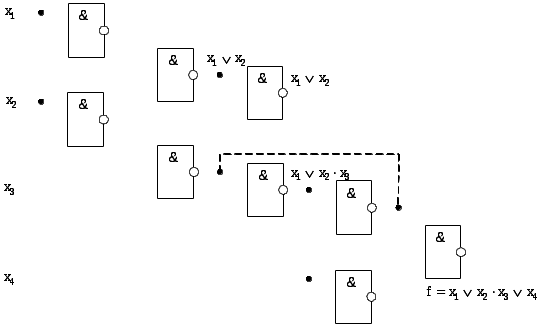
Рис. 15. Реализация функции
4.7Построение схемы в базисе Вебба {ИЛИ-НЕ}
Схема, реализующая функцию
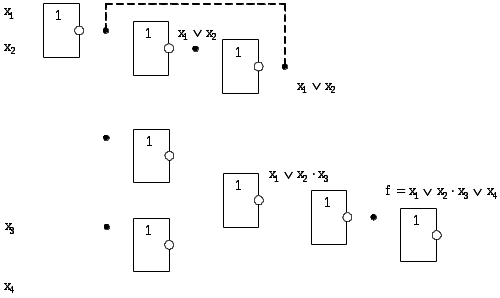
Рис. 16. Реализация функции
4.8Запись исходной формулы в базисе И, НЕ
Воспользовавшись законами алгебры логики (подразд. 2.2), преобразуем исходную функцию к виду, содержащему только функции И, НЕ:
4.9Запись исходной формулы в базисе ИЛИ, НЕ
Воспользовавшись законами алгебры логики (подразд. 2.2), преобразуем исходную функцию к виду, содержащему только функции ИЛИ, НЕ:
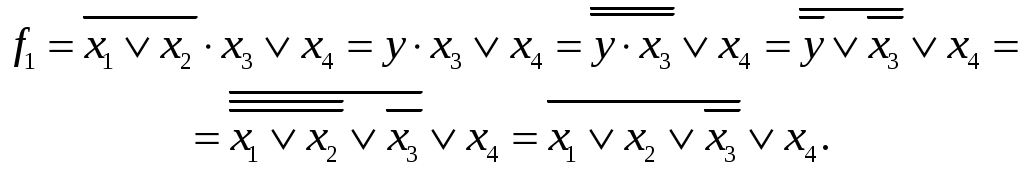
4.10Минимизация по картам Карно
Минимизируем функцию
Результат минимизации представлен на рис. 17.
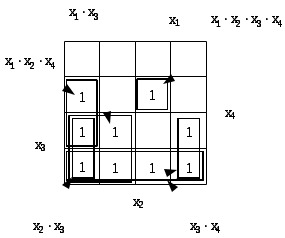
Рис. 17. Минимизация f2 по карте Карно
Запишем ФАЛ, соответствующую произведенной минимизации:
5Варианты заданий
Варианты заданий представлены в таблице 7.
Таблица 7
Варианты заданий
| Номер варианта | Функция f1 | Функция f2 |
| 1 | 2 | 3 |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
| 6 | | |
| 7 | | |
| 8 | | |
| 9 | | |
| 10 | | |
| 11 | | |
| 12 | | |
| 13 | | |
| 14 | | |
| 15 | | |
| 16 | | |
| 17 | | |
| 18 | | |
| 19 | | |
| 20 | | |
| 21 | | |
| 22 | | |
| 23 | | |
| 24 | | |
| 25 | | |
| 26 | | |
| 27 | | |