ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 192
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1Понятие комбинационной схемы и функции алгебры логики
2.3Реализация функций алгебры логики
2.4Минимизация ФАЛ с помощью карт Карно
4.2Построение релейно-контактной схемы
4.3Построение таблицы истинности
4.5Построение схемы в базисе {И, ИЛИ, НЕ}
4.6Построение схемы в базисе Шеффера {И-НЕ}
4.7Построение схемы в базисе Вебба {ИЛИ-НЕ}
4.8Запись исходной формулы в базисе И, НЕ
4.9Запись исходной формулы в базисе ИЛИ, НЕ
Федеральное агентство железнодорожного транспорта
Федеральное государственное образовательное учреждение
высшего профессионального образования
«петербургский государственный университет путей сообщения»
Кафедра «Автоматика и телемеханика на железных дорогах»
АНАЛИЗ И СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
Методические указания по курсу
«Теория дискретных устройств»
№1
Санкт-Петербург
ПГУПС
2011
1Цель работы
Изучение особенностей функций алгебры логики (ФАЛ), построение логических схем по заданной формуле с использованием различных элементных базисов, изучение методов преобразования ФАЛ, освоение методов минимизации ФАЛ с помощью карт Карно.
2Основные понятия
2.1Понятие комбинационной схемы и функции алгебры логики
Комбинационной логической схемой (КС)называется схема, значение сигнала на выходе которой в любой момент времени однозначно определяется значением сигналов на её входах.
Комбинационная логическая схема имеет n входов и один выход y (рис. 1). Входы и выходы являются двоичными, т. е. могут принимать только два значения: 0 или 1. Внутренняя структура КС построена также на двоичных элементах.
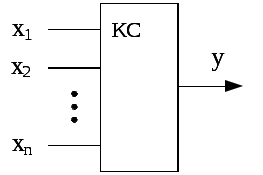
Рис. 1. Комбинационная схема с n входами
Примером двоичного входа является кнопка x, которая может быть нажата (x = 1) или не нажата (x = 0), а примером двоичного выхода – лампочка y, которая может гореть (y = 1) или не гореть (y = 0).
Математическим аппаратом для описания КС являются ФАЛ (булевы функции). ФАЛ от n переменных f(x1, x2, …, xn) можно задать с помощью таблицы истинности (табл. 1).
Таблица 1
Таблица истинности
| № | x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
Таблица содержит восемь строк, каждая из которых соответствует одному из возможных состояний всех трех кнопок x1, x2, x3. Значение y в строке определяет состояние лампочки при данном состоянии входов (рис. 2). Например, запись в строке № 0 означает, что если все три кнопки не нажаты (x1= x2= x3=0), то лампочка горит (y=1).
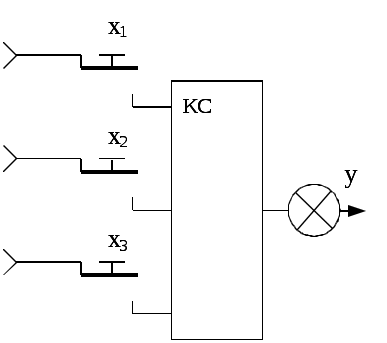
Рис. 2. Комбинационная схема
Особенностью ФАЛ является то, что все переменные и сами функции принимают только два значения. Областью определения ФАЛ от n переменных является множество двоичных наборов, число которых равно 2n. Каждому двоичному набору сопоставляется нулевое или единичное значение функции. Соответственно областью значений ФАЛ является множество {0, 1}.
Задать ФАЛ можно перечислением тех двоичных наборов, на которых функция равна 1. Эти наборы называются разрешенными. Например, функция y из таблицы 1 задается множеством (000, 011, 100, 110). Каждый двоичный набор N есть некоторое двоичное число, которое может быть переведено в десятичное по формуле:
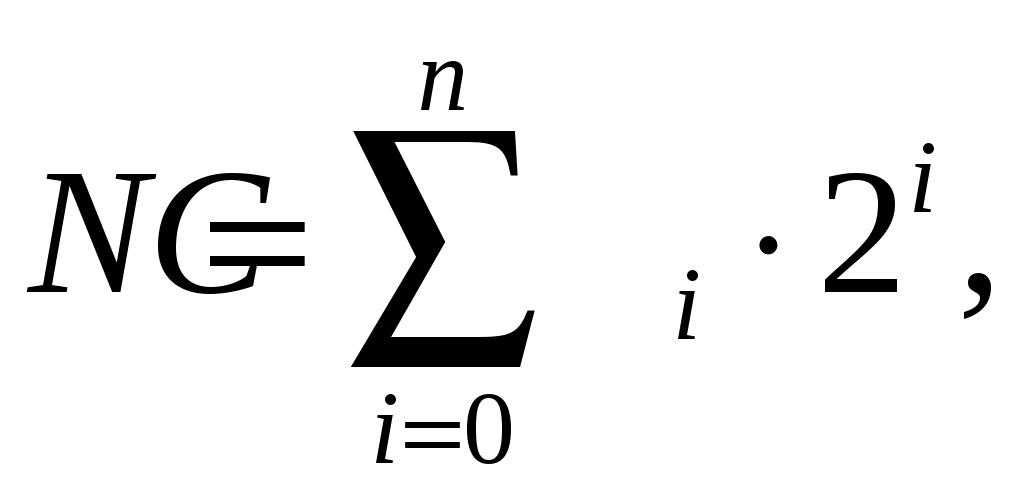 (1)
(1)где i – номер разряда, i = 0, 1, 2, …, n;
Ci – коэффициент при i-м разряде, Ci= 0или 1;
2i – вес i-го разряда.
Например,
В таблице 1 в левом крайнем столбце приведены десятичные эквиваленты двоичных чисел. Таким образом, ФАЛ можно задать также с помощью множества десятичных чисел, соответствующих разрешенным двоичным наборам. Например, функция y из таблицы 1 задается следующим множеством: (0,3,4,6).
Можно показать, что число ФАЛ от nпеременных равно
Функции И, ИЛИ, НЕ задаются соответственно таблицами 2, 3, 4, из которых следует их содержательный смысл. Функция И равна 1 только тогда, когда обе переменные равны 1. Обозначается следующим образом:
Функция ИЛИ равна 1, если хотя бы одна из переменных равна 1. Обозначается следующим образом:
Функция НЕ принимает значение, противоположное значению входной переменной. Обозначается следующим образом:
Таблица 2
Таблица истинности функции И
| № | x1 | x2 | y |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
Таблица 3
Таблица истинности функции ИЛИ
| № | x1 | x2 | y |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 |
Таблица 4
Таблица истинности функции НЕ
| № | x | y |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Введение специальных знаков логических операций И, ИЛИ, НЕ позволяет задавать ФАЛ в алгебраической форме.
Рассмотрим, например, функцию
Для того чтобы перейти от алгебраической записи ФАЛ к таблице истинности, используют аксиомы алгебры логики, вытекающие непосредственно из таблиц 2, 3, 4:
Рассчитаем, например, значение функции (5) при x1=1, x2=0, x3=1:
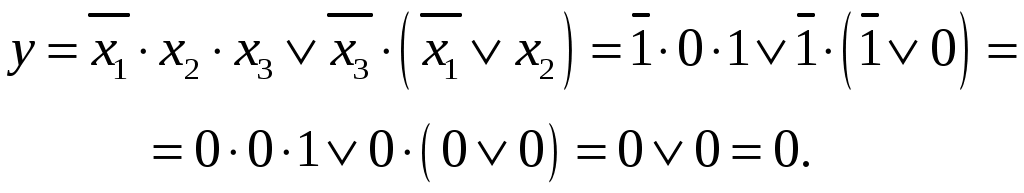 (9)
(9)Если рассчитать подобным образом значение функции на всех наборах, то получим таблицу истинности (таблица 1).
Доказательство того факта, что система функций И, ИЛИ, НЕ образует базис, состоит в указании алгоритма обратного перехода от таблицы истинности к алгебраической формуле, содержащей знаки только трех операций {И, ИЛИ, НЕ}. Этот алгоритм заключается в следующем:
-
в таблице истинности выбираются все наборы, на которых функция равна 1; -
выписываются конъюнкции, соответствующие этим наборам. При этом, если переменная x1 входит в данный набор как 0, то она записывается с отрицанием, в противном случае она записывается без отрицания; -
все полученные конъюнкции соединяются между собой знаками дизъюнкции.
Применение данного алгоритма к таблице 1 дает следующий результат:
Полученная форма записи ФАЛ называется дизъюнктивной совершенной нормальной формой (ДСНФ).
Переход от таблицы истинности к алгебраической записи может быть осуществлен с использованием другого алгоритма:
-
в таблице истинности выбираются все наборы, на которых функция равна 0 (такие наборы называются запрещенными); -
выписываются дизъюнкции, соответствующие этим наборам. При этом, если переменная x1 входит в данный набор как 0, то она записывается без отрицания, в противном случае она записывается с отрицанием; -
все полученные дизъюнкции соединяются между собой знаками конъюнкции.
Применение данного алгоритма к таблице 1 дает следующий результат:
Полученная форма записи ФАЛ называется конъюнктивной совершенной нормальной формой (КСНФ).