ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра «Теплотехника и гидравлика»


ГИДРАВЛИЧЕСКИЙ РАСЧЕТ НЕРАЗВЕТВЛЕННОГО ТРУБОПРОВОДА
Методические указания и задания к выполнению практической работы по гидравлике

(для студентов вечерних факультетов)


РПК «Политехник»

Волгоград 2009

УДК 532.542

Гидравлический расчет неразветвленного трубопровода: метод. указ. и задания к выполнению практической работы по гидравлике (для студентов вечерних факультетов) / сост.: Е. А. Федянов, А. А. Буров, В. А. Горюнов; Волгоградский гос. тех. ун-т. – Волгоград, 2009. – 30 с.
Излагаются теоретические основы решения инженерных задач по гидравлическому расчету неразветвленных трубопроводов. Даются задания и методические указания для выполнения студентами расчетно-графической работы. Приводятся необходимые справочные данные. Рассматриваются примеры решения типовых задач. Содержатся контрольные вопросы для проверки усвоения теоретического материала.

Методические указания предназначены для студентов вечерних факультетов.

Ил. Табл. 8. Библиогр.: 4 назв.

Рецензент Е. А. Дьячков

Печатается по решению редакционно-издательского совета ВолгГТУ
© Волгоградский

государственный

технический

университет

1. ЦЕЛЬ РАБОТЫ

1.1. Овладение методикой расчета неразветвленных трубопроводов.

1.2. Приобретение практических навыков использования справочных данных для определения гидравлических потерь.
2. СОДЕРЖАНИЕ РАБОТЫ

2.1. Расчет заданного варианта неразветвленного трубопровода.

2.2. Графическое построение линии полного напора и анализ изменения по длине трубопровода энергии потока.
3. ОСНОВНЫЕ ТИПЫ ЗАДАЧ И МЕТОДЫ ИХ РЕШЕНИЯ

Гидравлический расчет трубопровода основывается на двух уравнениях – уравнении Бернулли для потока реальной жидкости (3.1) и уравнении неразрывности потока (3.2), составленных для двух сечений трубопровода:

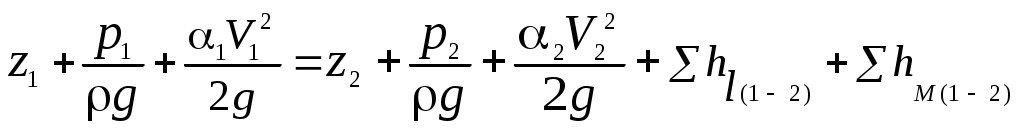, (3.1)

, (3.2)

где z₁, z₂ – вертикальные координаты потока соответственно в 1-м и 2-м сечении (расстояния от плоскости сравнения до центров тяжести сечений), м; р₁, р₂ – средние давления в центрах тяжести, соответственно 1-го и 2-го сечения потока, Па; α

---

₁ и α₂ – коэффициенты кинетической энергии (коэффициенты Кориолиса), соответственно для 1-го и 2-го сечения; V₁ и V₂ – средние скорости в первом и втором сечениях, м/с; ρ – плотность жидкости, кг/м³; g – ускорение свободного падения, м/с²; – потери напора по длине на участке между сечениями 1 и 2 (участок 1-2), м; – потери напора в местных сопротивлениях на участке 1-2, м; Q – объемный расход жидкости, м³/с; s₁ и s₂ – площади поперечных сечений, м².

В общем случае, когда трубопровод на участке 1-2 состоит из n последовательно соединенных труб различного диаметра, величина потерь по длине определяется по формуле:

, (3.3)

где l_i – длина i-й трубы постоянного диаметра d_i; λ_i – коэффициент потерь на трение в трубе диаметром d_i.

Коэффициент потерь на трение в общем случае зависит от значения числа Рейнольдса

Re = , (3.4)

где ν – кинематический коэффициент вязкости, м/с², и от относительной шероховатости внутренней поверхности трубы , где Δ – абсолютная шероховатость, м.

Величина коэффициента потерь на трение λ может быть определена по соответствующим графикам (например, по графику Мурина) или формулам. Для ламинарного течения (при Re < 2300)

. (3.5)

Для турбулентного течения (при Re > 2300) коэффициент потерь на трение может быть определен, например, по универсальной формуле Альтшуля:

---

. (3.6)

Величина потерь в каждом из местных сопротивлений определяется по формуле:

, (3.7)

где ξ_м – коэффициент потерь для данного местного сопротивления. Величина общих потерь в m местных сопротивлениях на участке 1-2 находится суммированием потерь, подсчитанных по формуле 3.7 для каждого местного сопротивления:

= (3.8)

Численные значения коэффициентов местных сопротивлений определяются в зависимости от типа сопротивления и режима течения по формулам или таблицам, приводимым в справочной литературе. Некоторые формулы и таблицы приведены в приложении 1.

В практике гидравлического расчета трубопроводов встречаются три основных типа задач.

В задачах первого типа определяется величина потребного напора H или давления p₁, которые необходимо создать в начале трубопровода. Исходными данными для расчета являются: расход Q, давление р₂, свойства жидкости, размеры трубопровода и шероховатость Δ труб.

В задачах второго типа определяется расход Q жидкости. Исходными данными для расчета являются: давления р₁ и р₂, свойства жидкости, размеры трубопровода и шероховатость Δ труб.

В задачах третьего типа требуется определить неизвестный диаметр d трубы. Исходными данными для расчета являются: расход Q, давления р₁ и р₂, свойства жидкости, шероховатость Δ труб и размеры трубопровода за исключением неизвестного диаметра трубы.

При решении всех трех типов задач используется уравнение Бернулли (3.1). Важно правильно выбрать два сечения, для которых это уравнение будет записано (сечения нумеруются по ходу движения жидкости). В качестве таких сечений рекомендуется брать:

1. Свободную поверхность жидкости в резервуаре (баке), где V ≈ 0, поскольку площадь сечения резервуара во много раз больше площади любого поперечного сечения трубопровода;

2. Выход в атмосферу, где р_изб = 0, а р_абс = р_ат;

3. Сечение на выходе из насоса.

Уравнение Бернулли рекомендуется сначала записать в общем виде (3.1), а затем переписать с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

---

Необходимо также иметь в виду:

1. Плоскость сравнения для отсчета ординаты z целесообразно выбирать таким образом, чтобы она проходила через центр тяжести нижнего сечения. Тогда для этого сечения z = 0;

2. Давления р₁ и р₂ в обеих частях уравнения должны быть заданы в одной системе отсчета (или абсолютные, или избыточные);

3. Потери энергии всегда записываются в правой части уравнения Бернулли со знаком «+»;

4. Значения всех величин должны быть выражены в основных единицах международной системы (СИ): линейные размеры – в метрах (м), расход – в кубометрах за секунду (м³/с), давление – в паскалях (Па).
Решение задач первого типа. Вычисляется число Рейнольдса (3.4) и определяется режим течения. По соответствующим формулам и таблицам (см. приложение 1) определяются значения коэффициентов местных сопротивлений. Определяются потери напора в каждом из местных сопротивлений (3.7) и суммарные потери (3.8). Коэффициент потерь по длине определяется в зависимости от величины числа Рейнольдса и величины шероховатости по формулам (3.5) или (3.6). Определяют потери напора по длине (3.3). Решают основное уравнение (3.1) относительно искомой величины.

Решение задач второго типа. Значение числа Рейнольдса не может быть найдено по исходным данным. Поэтому используется метод последовательных приближений.

Значение коэффициентов потерь по длине (λ_i) и коэффициентов местных сопротивлений (ξ_i) в первом приближении определяют исходя из предположения, что режим течения соответствует области квадратичного сопротивления.

Значение λ для каждого участка трубопровода определяют по формуле Шифринсона:

. (3.9)

На базе основного уравнения (3.1) находят расход Q и далее число Рейнольдса Re (3.4) в первом приближении. В соответствии с найденным значением Re определяют λ (по формуле 3.5 или 3.6) и Qво втором приближении. Полученное значение Q сравнивают с предыдущим. Если расхождение оказывается больше заданной (допустимой) ошибки расчета, находят третье приближенное значение расхода. Расчеты заканчивают тогда, когда расхождение становится меньше заданной ошибки.

Решение задач третьего типа

---

. Задача третьего типа может быть решена как методом последовательных приближений (см. решение задач второго типа), так и графо-аналитическим методом. Сущность графо-аналитического метода пояснена соответствующим примером в приложении 2.
4. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКОЙ РАБОТЫ

Ниже приводятся схемы трубопроводов (рис. 4.1 – рис. 4.10), для которых в таблицах (табл. 4.1 – табл. 4.3) даются необходимые данные для расчетов.

Требуется определить неизвестный параметр, отмеченный в таблицах знаком вопроса («?») и построить в масштабе на миллиметровой бумаге линию полного напора.

ПРИМЕЧАНИЯ.

1. Жидкость в трубопроводы, изображенные на рисунках 4.2, 4.3 и 4.8, поступает от насосов, на выходе каждого из которых давление равно р_м.

2. При решении задач третьего типа, выбирая окончательный диаметр трубы, считать, что труба стальная водогазопроводная (ГОСТ 3262-75).

3. Установленный на трубопроводе вентиль полностью открыт.

4. При вычислении величины местных потерь считать, что местные сопротивления не оказывают взаимного влияния друг на друга.



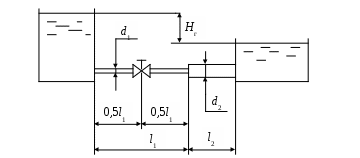
Рис. 4.1



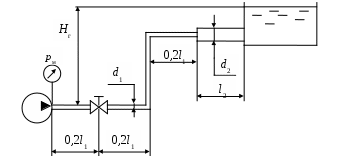
Рис. 4.2



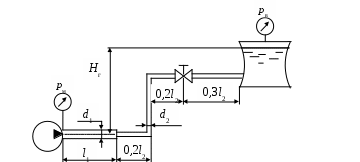
Рис. 4.3



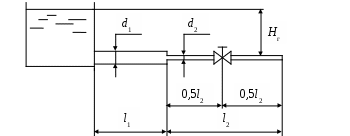
Рис. 4.4



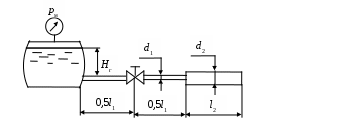
Рис. 4. 5



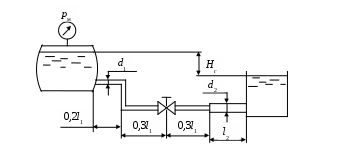
Рис. 4.6


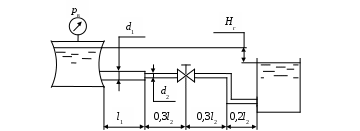
Рис. 4.7




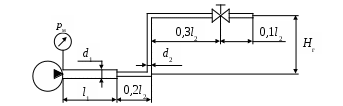
Рис.4.8


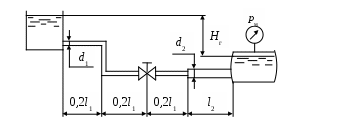
Рис. 4.9


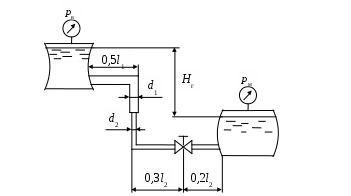
Рис.4.10

Таблица 4.1

Вариант	Рисунок	Трубы					Q	pм	pв	Hг	Жидкость	Тем- пера- тура
		l1	l2	d1	d2	Δ	дм3/с (л/с)	МПа	МПа	м
		м	м	мм	мм	мм						оС
1	4.1	10	20	40	50	0,05	5,0	–	–	?	Циклопентан	10
2	4.1	8	15	32	40	0,08	3,0	–	–	?	Вода	5
3	4.1	6	10	25	32	0,1	2,0	–	–	?	Керосин	20
4	4.2	10	3	50	65	0,1	4,0	?	–	6	Вода	10
5	4.2	8	5	40	50	0,15	2,5	?	–	5	Бензин	15
6	4.2	10	10	32	50	0,07	2,0	?	–	7	Спирт этил.	20
7	4.3	5	10	90	80	0,15	5,5	?	0,02	5	Вода	15
8	4.3	4	5	80	65	0,2	4,5	?	0,01	3	Керосин	20
9	4.3	3	8	65	40	0,25	3,5	?	0,01	4	Спирт метил.	15
10	4.4	25	15	85	45	0,05	4,0	–	–	?	Вода	30
11	4.4	28	18	100	50	0,08	4,0	–	–	?	Циклопентан	20
12	4.4	30	20	105	52	0,1	4,4	–	–	?	Анилин	10
13	4.5	10	10	32	40	0,4	3,2	0,08	–	?	Вода	20
14	4.5	20	15	40	50	0,5	3,8	0,02	–	?	Диз. топливо	20
15	4.5	24	10	50	65	0,4	4,2	0,01	–	?	Бензин	20
16	4.6	20	15	65	80	0,3	5,0	0,01	–	?	Вода	40
17	4.6	30	24	80	90	0,4	7,0	0,01	–	?	Спирт этил.	20
18	4.6	10	10	65	100	0,5	9,0	0,08	–	?	Глицерин	40
19	4.7	4	5	32	25	0,2	2,5	–	0,01	?	Вода	10
20	4.7	6	5	50	32	0,3	3,5	–	0,02	?	Керосин	20
21	4.7	8	10	80	50	0,4	4,5	–	0,03	?	Спирт метил.	15
22	4.8	5	20	100	80	0,07	8,5	?	–	8	Вода	20
23	4.8	8	10	90	65	0,06	7,5	?	–	4	Диз. топливо	20
24	4.8	2	5	50	32	0,05	6,0	?	–	2	Глицерин	20
25	4.9	5	5	40	65	0,3	6,5	0,02	–	?	Вода	30
26	4.9	5	10	50	80	0,4	7,0	0,05	–	?	Анилин	10
27	4.9	10	15	65	100	0,5	7,5	0,04	–	?	Бензин	15
28	4.10	2	5	150	100	0,5	10	0,05	0,01	?	Вода	10
29	4.10	4	4	125	90	0,4	8,0	0,06	0,02	?	Керосин	20
30	4.10	2	6	100	80	0,3	6,0	0,07	0,01	?	Спирт этил.	20

---

Смотрите также файлы

• Курсовая работа по дисциплине Информатика и компьютерные технологии на транспорте.docx

• Показательные уравнения.docx

• Обучающийся Лучших Ирина Борисовна Преподаватель Чащинова Анна Вадимовна Практическое занятие.doc

• Организационная деятельность государственной противопожарной службы мчс россии.docx

• Внутренняя опись документов, находящихся в отчете.docx