Задание. Определить давление р_м для трубопровода, схема которого представлена на рис. П.2.1.

Исходные данные. Q = 1,2·10^-3м³/с; l₁ = 5 м; l₂ = 5 м; d₁ = 20 мм; d₂ = 40 мм; Δ = 0,05 мм; H_г = 10 м; р_в = 0,03 МПа; жидкость – бензин; t =15^о С.



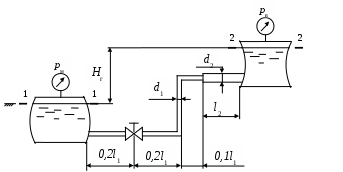
Рис. П.2.1
Решение. Пусть плоскость сравнения совпадает с уровнем жидкости в нижнем резервуаре, сечение 1-1 совпадает с плоскостью сравнения, а сечение 2-2 совпадает с уровнем жидкости в верхнем резервуаре. Тогда z₁ = 0, z₂ = H_г.

Допускаем, что V₁ ≈ 0 и V₂ ≈ 0, поскольку площади сечений резервуаров во много раз больше площадей поперечных сечений трубопровода. Абсолютные давления в сечениях 1-1 и 2-2 соответственно равны:

р₁ = р_ат + р_м , р₂ = р_ат – р_в.

Подставляя полученные значения параметров в уравнение Бернулли (3.1) получим:

, (П2.1)

откуда:

.

Потери напора в рассматриваемом трубопроводе включают потери по длине на участках с диаметрами d₁ и d₂, а также местные потери при входе жидкости из нижнего резервуара в трубопровод, в вентиле, при резком повороте (два поворота), при внезапном расширении, при выходе жидкости из трубопровода в верхний резервуар. Выражение для потерь напора запишется следующим образом:

.

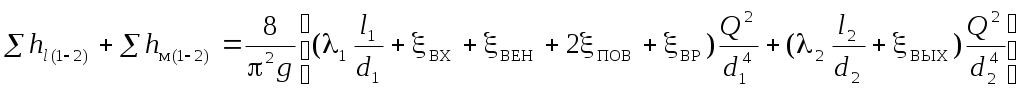Окончательное выражение для искомого параметра приобретает вид:

.

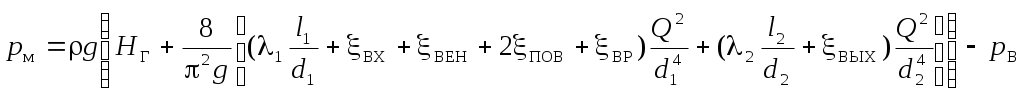По формуле (3.4) определяем значения чисел Рейнольдса (значение вязкости взято из табл. П1.1):

Re₁ = = = 82186,

Re₂ = =

---

= 41093.

Так как режим течения турбулентный (Re > 2300), то коэффициенты потерь на трение могут быть найдены по формуле Альтшуля (3.6).

Имеем:

= 0,0264,

= 0,0255.

Определяем значения коэффициентов местных сопротивлений (табл. П1.2):

ξ_вх = 0,5; ξ_вен = 5; ξ_пов = 1,1; ξ_вых = 1; ξ_вр = 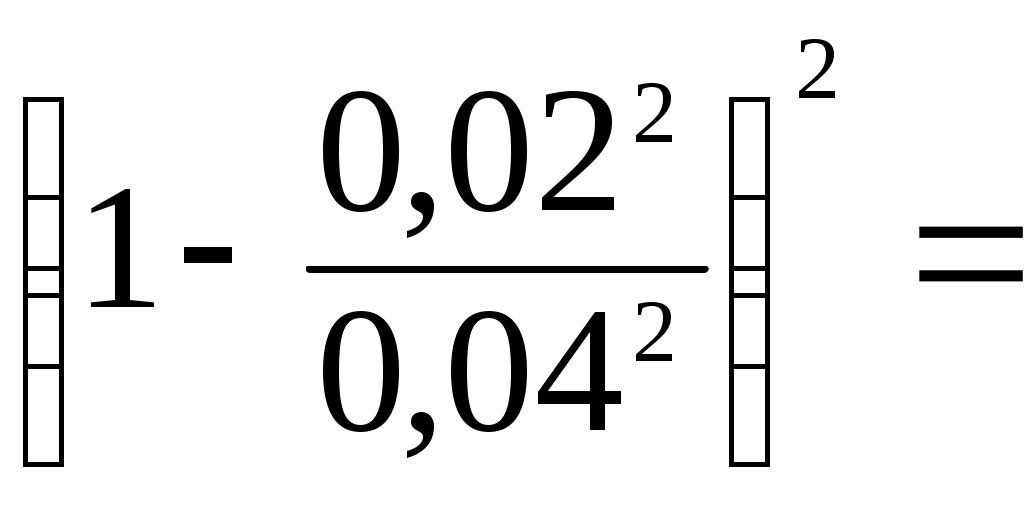0,563.

Вычисляем искомый параметр:

р_м = 750·9,81{ [ +

+ ]} – 0,03·10⁶ = 126400 (Па) = 0,1264 (МПа)
П.2.1.2. Задача второго типа

Задание. Определить расход Q для трубопровода, схема которого представлена на рис. П2.1.

Исходные данные. l₁ = 5 м; l₂ = 6 м; d₁ = 20 мм; d₂ = 40 мм; Δ = 0,01 мм; H_г = 8 м; p_м = 0,1 МПа; р_в = 0,03 МПа; жидкость – анилин; t =10^о С.

Решение. Выбираем плоскость сравнения и два сечения, для которых записываем уравнение Бернулли. Упрощаем уравнение и записываем выражение для суммарных потерь напора (см. пример решения задачи первого типа). Выражаем в общем виде искомый параметр:

Q = .

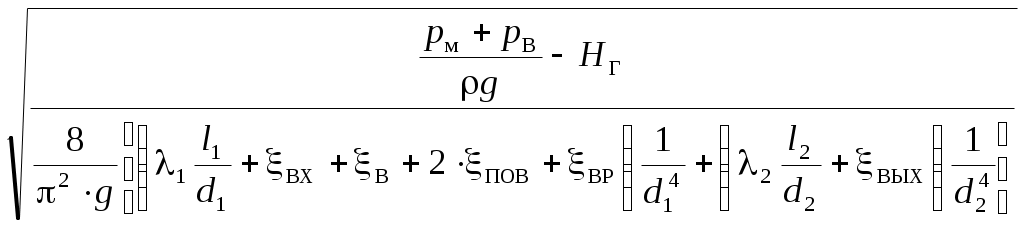Предполагая, что в первом приближении режим течения соответствует области квадратичного сопротивления, по формуле Шифринсона (3.9) определяем значения λ:

= 0,016,

= 0,014.

Определяем значения коэффициентов местных сопротивлений (табл. П1.2):

ξ_вх = 0,5; ξ_вен = 5; ξ_пов = 1,1; ξ_вых = 1; ξ_вр =

---

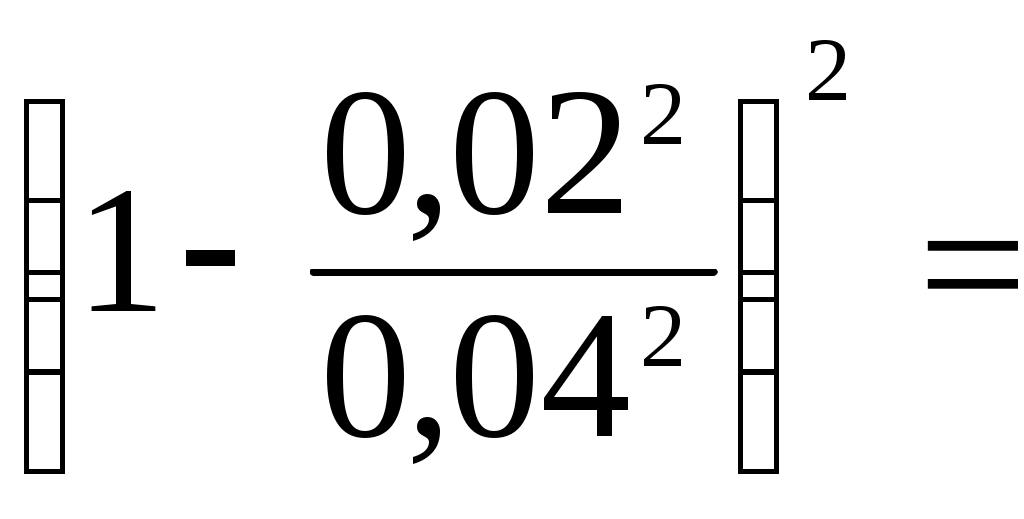
0,563.

Вычисляем в первом приближении значение расхода:

Q₁ = =

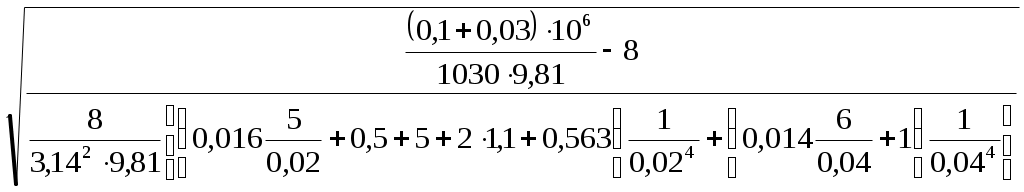= 0,87·10^-3 м³/с .

Используя найденное значение расхода, определяем величину чисел Рейнольдса (3.4) и коэффициентов потерь по длине (3.6):

Re₁ = = 8782, Re₂ = = 4391,

= 0,033,

= 0,039.

Находим второе приближение для величины расхода:

Q₂ = =

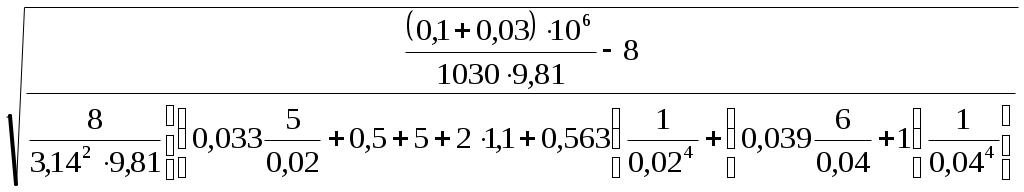= 0,746·10^-3 (м³/с).

Сравнивая полученное значение с предыдущим, имеем:

.

Если принять, что ошибка расчетов не должна превышать 10%, то, очевидно, требуется найти еще одно приближение для Q.

Выполняя расчеты в приведенной выше последовательности, находим:

Re₁ = = 7530, Re₂ = = 3765,

= 0,034,

= 0,04.

Q₃ = =

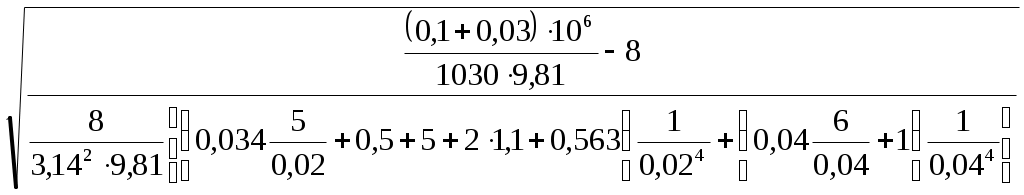= 0,74·10^-3 (м³/с).

Сравнивая полученное значение с предыдущим, имеем:

.

Расхождение результатов расчета (0,8%) меньше допустимой ошибки (10%).

Таким образом, окончательно принимаем Q = 0,74·10^-3 м³/с.
П.2.1.3. Задача третьего типа

Задание. Определить диаметр d₂ для трубопровода, схема которого представлена на рис. П2.1.

Исходные данные. l₁ = 6 м; l₂ = 8 м; d₁ = 25 мм; Q = 1·10^-3м³/с; Δ = 0,2 мм; H_г = 6 м; p_м = 0,07 МПа; р_в = 0,03 МПа; жидкость – вода; t =20^о С.

Решение. Выбираем плоскость сравнения и два сечения, для которых записываем уравнение Бернулли. Упрощаем уравнение и записываем выражение для суммарных потерь напора (см. пример решения задачи первого типа).

---

Получим:

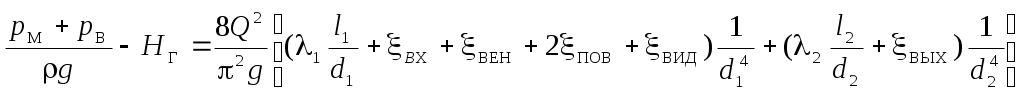, (П1)

где ξ_вид – коэффициент местного сопротивления при внезапном изменении диаметра трубы. При уменьшении диаметра ξ_вид = ξ_вс (внезапное сужение), при увеличении диаметра ξ_вид = ξ_вр (внезапное расширение).

Для участка трубопровода известного диаметра d₁ определяем значение числа Рейнольдса (ф. 3.4):

Re₁ = = 50451.

Так как Re₁ > 2300, режим течения – турбулентный, поэтому коэффициент потерь на трение находим по формуле Альтшуля (3.6):

= 0,034.

Значения коэффициентов местных сопротивлений (табл. П1.2):

ξ_вх = 0,5; ξ_вен = 5; ξ_пов = 1,1; ξ_вых = 1.

Подставляем известные величины в уравнение (П1)

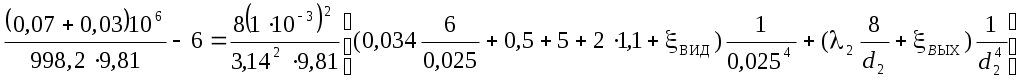и после упрощения получаем:

. (П2)

Полученное уравнение удобно решать графо-аналитическим методом. Для этого подсчитаем значение правой части уравнения (П2) для ряда значений диаметра d₂.

Задаем первое значение диаметра d₂ = 0,01 м. Определяем для этого диаметра неизвестные значения параметров:

Re₂ = = 126127,

= 0,042,

ξ_вид = ξ_вс = 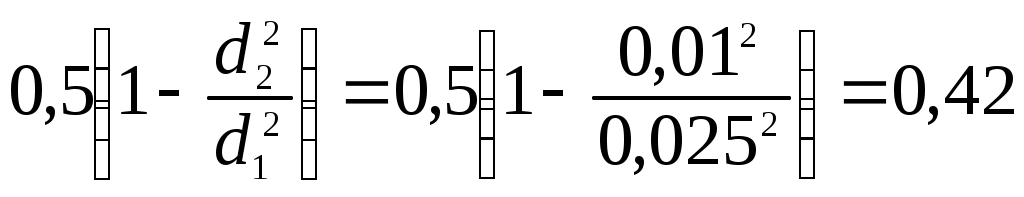, ξ_вых = 1.

Подсчитываем величину правой части уравнения (П2), которая представляет собой сумму потерь:

= 289,6 (м).

Аналогичным образом находим значения суммарных потерь для других диаметров, обращая особое внимание на вычисление коэффициента ξ_вид .

Получим:

для d₂ = 0,02 м м,

для d₂ = 0,03 м м,

для d₂ = 0,04 м м.

---

Строим график f(d₂) (рис. П2.2). С помощью графика находим величину диаметра d₂ = 30 мм, удовлетворяющую уравнению (П2).

ГОСТ 3262-75 «Трубы стальные водогазопроводные» предусматривает следующие величины внутренних диаметров труб (мм): 6, 8, 10, 15, 20, 25, 32, 40, 50, 65, 80, 90, 100, 125, 150.

Окончательно принимаем: d₂ = 32 мм.

ВНИМАНИЕ! При расчетах не забывайте перевести: линейные размеры, выраженные в миллиметрах – в метры (1 мм = 10^-3 м); расход, выраженный в кубических дециметрах за секунду – в кубометры за секунду (1 дм³/с = 10^-3 м³/с); давление, выраженное в мегапаскалях – в паскали (1 МПа = 10⁶ Па).



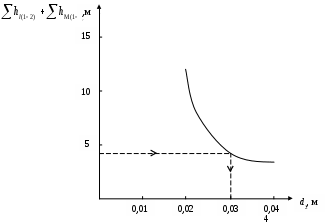
Рис. П2.2
П2.2. ПОСТРОЕНИЕ ЛИНИИ ПОЛНОГО НАПОРА

Рассмотрим пример построения линии полного напора применительно к задаче первого типа. Для задач второго и третьего типов такие построения выполняются аналогично.

Полный напор в сечении 1-1определяется по формуле:

.

Так как z₁ = 0 и V₁ ≈ 0, р_ат = 9,81·10⁴ Па, то

(м).

Находим величину полного напора в других характерных сечениях трубопровода (рис. П2.3):

H_A = H₁ – h_вх = H₁ -

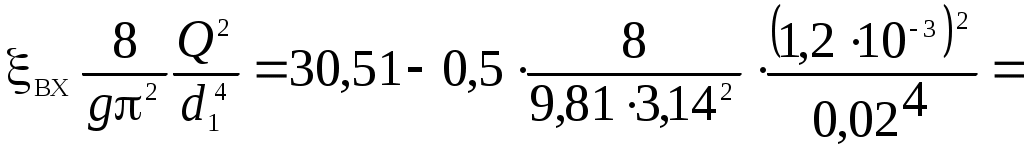
= 30,51 – 0,37 = 30,14 (м).

H_В = H_A – 0,2·h_l1 = = =

= 30,14 – 0,98 = 29,16 (м).

H_С = H_В – h_вен = H_В -

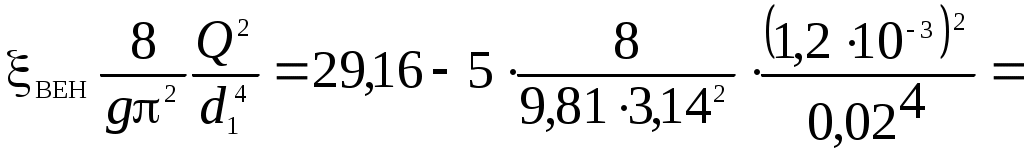
= 29,16 – 3,72 = 25,44 (м).

H_D = H_C – 0,2·h_l1 = 25,44 – 0,98 = 24,46 (м).

H_E = H_D– 0,5·h_l1 – 2·h_пов = H_D – =

=

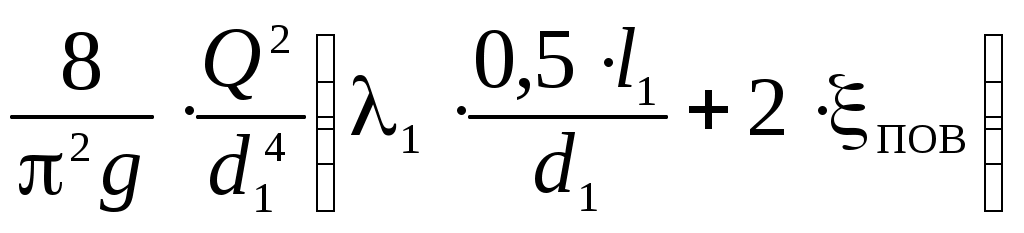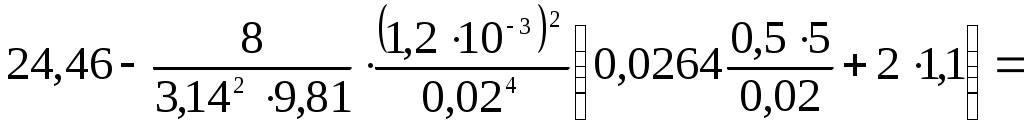
= 24,46 – 4,09 = 20,37 (м).

H_F = H_E – 0,1·h_l1 = 20,37– = 20,37 – 0,49 = 19,88 (м).

H_G = H_F

---

Смотрите также файлы

• Курсовая работа по дисциплине Информатика и компьютерные технологии на транспорте.docx

• Показательные уравнения.docx

• Обучающийся Лучших Ирина Борисовна Преподаватель Чащинова Анна Вадимовна Практическое занятие.doc

• Организационная деятельность государственной противопожарной службы мчс россии.docx

• Внутренняя опись документов, находящихся в отчете.docx