Реферат

Основные типы дифференциальных уравнений первого порядка
1. Уравнения с разделяющимися переменными
Рассмотрим уравнение
X(x)dx+Y(y)dy=0, (1)
в котором коэффициент при dx зависит только от x, а коэффициент при dy - только от y. Такое уравнение называется уравнением с разделенными переменными.

Будем предполагать, что функции X(x) и Y(y) непрерывны при всех рассматриваемых значениях x и y. Тогда уравнение (1) можно переписать так

. (2)
Поэтому

. (3)
Это есть общий интеграл уравнения (1). Особых решений нет.

К уравнению с разделенными переменными легко приводится уравнение вида
p₁(x)p₂(y)dx + q₁(x)q₂(y)dy = 0
в котором коэффициенты при dx и dy представляют собой произведения функции от x на функцию от y.

Определение 1.: Уравнение вида
P (x, y)dx + Q (x, y)dy = 0 (4)
называется уравнением с разделяющимися переменными, если функции P(x,y) и Q(x,y) можно представить в следующем виде P(x,y) = p₁(x)p₂(y), Q(x,y) = q₁(x)q₂(y).

В точках, где p₂(y) № 0 и q₁(x) № 0, переменные x и y можно отделить друг от друга, разделив обе части уравнения
p₁(x)p₂(y)dx + q₁(x)q₂(y)dy = 0
на произведение p₂(y)q₁(x):
.
Интегрируя, получим общий интеграл уравнения (4):
,
где С - произвольная постоянная.

Замечание. Если уравнение p₂(y)q₁(x) = 0 допускает решения x = a или y = b, то они, очевидно, являются решениями дифференциального уравнения (4), кроме точек пересечения прямых x = a и y = b, так как в этих точках уравнение (4) не определено. Если эти решения входят в общий интеграл, то каждое из них есть частное решение дифференциального уравнения (4), а если нет, то это особые решения.

Пример 1. Проинтегрировать уравнение .

Разделяя переменные, имеем:

.
Интегрируя почленно, получаем:

---

- общий интеграл решения.
Уравнение имеет решения , которые являются особыми, так как не получаются из общего интеграла ни при каких значениях произвольной постоянной и на каждом из них нарушается единственность решения задачи Коши.
. Однородные дифференциальные уравнения
Определение: Функция двух переменных f(x,y) называется однородной функцией степени однородности m, где m целое, если при любом k выполняется следующее равенство:
f (kx,ky) = k^mf (x,y).
Покажем, что всякую однородную функцию нулевой степени можно представить в виде функции отношения . Пусть f (x,y) - однородная функция нулевой степени. Возьмем множитель ; по определению однородности имеем: и в правой части действительно стоит функция только отношения . Пусть теперь f (x,y) - однородная функция степени m. Очевидно, что функция будет однородной функцией нулевой степени и по указанному выше можно написать: , откуда
. (5)
Это общий вид однородной функции степени m.

Определение: Однородным уравнением первого порядка называется уравнение вида
P (x,y)dx + Q (x,y)dy = 0 (6)
где P (x,y) и Q (x,y) - однородные функции одной и той же степени однородности.

Решение такого уравнения проводится путем введения новой переменной , с помощью которой уравнение превращается в уравнение с разделяющимися переменными. Действительно, пользуясь формулой (5), можно переписать однородное уравнение в следующем виде:

---

(7).
Предположим, что функции P(x,y) и Q(x,y) не содержат общего множителя x^k, ибо если бы такой множитель был, то уравнение распалось бы на два: х=0, . В этом случае второе уравнение уже не содержит множителя x^k.

Таким образом x^m № 0 и можем разделить обе части уравнения (7) на x^m:

Полагаем , откуда . Подставляя эти значения в последнее уравнение, имеем:

или
.
Получилось уравнение с разделяющимися переменными, которое решаем, как было указано выше:
,
отсюда

и, потенцируя, получаем: x=CЧw(t), где через w(t) обозначено все выражение, содержащее t в правой части. Заменяя t отношением , получаем окончательный вид общего интеграла:

x = CЧw( ).
Необходимо учитывать, что при делении на могут быть потеряны решения.

Интегральные кривые однородного уравнения обладают интересным геометрическим свойством: они все подобны друг другу и центр подобия находится в начале координат.

Пример 2. Решить уравнение .

В приведенных выше обозначениях обе функции являются однородными функциями второй степени

---

, следовательно, данное уравнение однородное. Вводим новую переменную, полагая y=tx. Тогда dy=tdx+xdt, и уравнение после подстановки имеет вид:

Разделяем переменные:

(так как делим только на x и на сумму квадратов , то потери возможных корней нет); затем, интегрируя, получаем
;

потенцируем

и заменяем t через :
.
Делаем преобразование
,


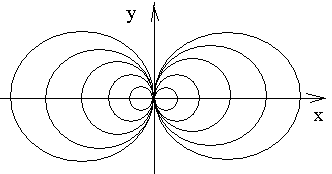
Рис. 1
После чего становится ясно, что имеем семейство окружностей с центрами в точках на оси Ox и с радиусами, равными . Все эти окружности касаются оси

Oy в начале координат и подобны друг другу (рис.1).

Рассмотрим уравнение вида

. (8)
Если с₁=с=0, то это уравнение однородное, ибо оно приводится к виду (6). Пусть хоть одно из чисел с₁, с отлично от нуля и предположим еще, что

Сделаем линейную замену обеих переменных:

Тогда наше уравнение примет вид:

Выбрав α и β так, чтобы

---

получим однородное уравнение


Интегрируя его и возвращаясь к переменным x и y, найдем общий интеграл уравнения (8).

Если же

то мы имеем , откуда a₁=ka, b₁=kb. Поэтому уравнение (8) можно переписать в этом случае так:
.
Введя здесь вместо y новую неизвестную функцию z по формуле
z=ax+by,
мы придем к уравнению, не содержащему независимой переменной:
.
Пример 3. Решить уравнение .

Заменяя y’ на получаем:

.
Введем вместо x и y переменные ξ и η, связанные с x и y линейной зависимостью
x=ξ+α, y=η+β,
вследствие чего dx=dξ, dy=dη. Постоянные α и β надо подобрать так, чтобы множители в уравнении при dξ, dη были однородными функциями первой степени. Для этого надо, чтобы в этих множителях

отсутствовали свободные члены, то есть чтобы было

Из этой системы уравнений находим: и подставляем их в формулы для x и y: . Заменяя x и y в данном уравнении, используя эти формулы, получаем однородное уравнение в переменных ξ и η:
.

Решаем это уравнение по правилам решения однородных уравнений, вводя переменную

---

Смотрите также файлы

• Отчетный период Отклонение, , Темп роста, Выручка, тыс руб. 285 940 355 940 70 000 124,5.docx

• П. А. Катенин Любовь.docx

• 2 У(региональный) Умышленное нанесение тяжкого вреда здоровью (( Нокнутое состояние )) 3 года лишения свободы.docx

• Казанский государственный энергетический.docx

• Учебного предмета модуль 1 Культура безопасности жизнедеятельности в современном обществе цель и задачи учебного предмета обж, его ключевые понятия и значение для человека.docx