Файл: 7. Исследование влияния параметров элементов цепи на форму ачх и фильтрующие свойства четырехполюсника.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 80
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
| Задание на курсовой проект…………………………………………….. | 3 |
| Введение………………………………………………………………… | 5 |
| 1. Составление схемы электрической цепи и запись уравнений Кирхгофа………………………………………………………………… | 7 |
| 2. Расчёт всех токов и напряжений схемы…………………………….. | 8 |
| 3. Построение топографической диаграммы напряжений и векторной диаграммы токов. Анализ результатов расчёта…………... | 12 |
| 4. Составление передаточной функции по напряжению для исследуемого четырехполюсника..…………...…………...………….... | 14 |
| 5. Расчёт и построение графиков для амплитудночастотной (АЧХ) и фазочастотной (ФЧХ) характеристик………………………………….. | 17 |
| 6. Анализ четырёхполюсника с точки зрения теории электрических фильтров…………………………………………………………………. | 19 |
| 7. Исследование влияния параметров элементов цепи на форму АЧХ и фильтрующие свойства четырехполюсника………………………… | 20 |
| 8. Исследование влияния сопротивления нагрузки на форму АЧХ и фильтрующие свойства четырехполюсника………………………….. | 29 |
| Заключение……………………………………………………………… | 32 |
| Библиографический список…………………………………………….. | 33 |
ЗАДАНИЕ НА КУРСОВОЙ ПРОЕКТ
К источнику синусоидальной ЭДС е(t)=Еm∙sinωt подключен четырехполюсник

Рисунок 1 – обобщенная схема исследуемой цепи
Схема четырёхполюсник согласно варианту изображена на рис.2.

Рисунок 2 – Схема четырёхполюсника
Амплитудное значение ЭДС: Еm = 10 В,внутреннее сопротивление источника: R
В=0.5кОм,частота: ω=2000 рад/с,активные сопротивления схемы: R=1 кОм, емкость конденсаторов: С=0,5 мкФ.
1. Изобразите схему электрической цепи согласно своему варианту. Составьте для нее систему уравнений по законам Кирхгофа.
2. При заданной частоте ω определите токи и напряжения на всех элементах схемы, пользуясь методом любым ранее изученным методом, мотивировав его рациональность. Вычислите входное и выходное напряжения и найдите соотношение между ними.В работе приведите подробное описание расчетов.
3. Постройте векторную диаграмму токов, совмещенную с топографической диаграммой, показав на ней напряжения всех элементов и участков. Проанализируйте сдвиги фаз междунапряжениями и токами на каждом элементе схемы и всей схемы в целом, проверьте соблюдение законов Кирхгофа.
Проанализируйте положение относительно друг другавекторов входного и выходного напряжений, сравните их длины, сделайте вывод о работе четырехполюсника на заданнойчастоте.
4. Составьте выражение для передаточной функции по напряжению для исследуемого четырехполюсника.
5. Получите аналитические выражения для амплитудночастотной (АЧХ) и фазочастотной (ФЧХ) характеристик.Постройте графики АЧХ и ФЧХ.Сделайте вывод о фильтрующей способности четырехполюсника.
6. Используя амплитудно-частотную характеристику,проанализируйте фильтрующие свойства четырехполюсника.Определите ширину полосы прозрачности фильтра.
7. Исследуйте влияние параметров элементов цепи наформу АЧХ и фильтрующие свойства четырехполюсника, отказавшись от равенства сопротивлений и емкостей.
8. Рассмотрите работу полученного фильтра при подключенном к выходу цепи сопротивлении нагрузки RН 100 кОм, 50кОм, 20 кОм, оцените влияние величины сопротивлениянагрузки RН на вид АЧХ, сделайте выводы по работе фильтра.
Введение
Простейшим среди фильтров является RC-фильтр. Принцип его работы основан на том, что при изменении частоты реактивное сопротивление конденсатора изменяется обратно пропорционально частоте, а сопротивление резистора остается неизменным.
Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам
Достоинствапассивных RC-фильтров:
-широкий частотный и динамический диапазон,
-хорошо проработанная теория на базе вековой практики,
-возможность реализации различных АЧХ И ФЧХ.
Недостатки пассивных RC-фильтров:
- Ослаблениесигнала,
- Малая крутизна АЧХ.
-большие масса и габариты,
-сложность и нетехнологичность изготовления,
-слабая помехоустойчивость к ЭМП,
-недостаточная стабильность и надежность,
-несовместимость с интегральной технологией.
Недостатки устраняются путём использования схем на операционных усилителях, так называемые ARC-фильтры, которые обладают лучшими характеристиками по сравнению с пассивными фильтрами.
RC-фильтры популярны –в силу простоты изготовления - по сравнению с фильтрами на основанными на катушках индуктивностей, кроме того RCфильтры имеют более низкие потери энергии по сравнению с теми же фильтрами на катушках.
1. Составление схемы электрической цепи и запись уравнений Кирхгофа

Рисунок 3 – Расчётная схема
Топологический анализ:
В схеме 3 узла, следовательно, число уравнений по 1 закону Кирхгофа
NI = 3-1 =2.
В схеме 3 независимых контура, следовательно, число уравнений по 2 закону Кирхгофа NII= 3.
Таким образом, общее число уравнений по законам Кирхгофа равно числу ветвей
Nв = NI + NII = 2 + 3 = 5.
На схеме обозначим узлы, токи ветвей и направления обхода контуров.
Уравнения по первому закону Кирхгофа для узлов 1 и 2:

Уравнения по второму закону Кирхгофа для контуров I, II и III:
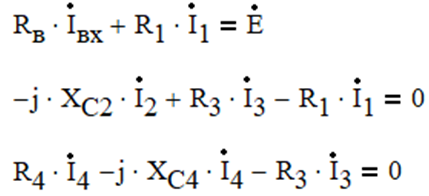
2. Расчёт всех токов и напряжений схемы.
Метод Кирхгофа – не оптимален так нужно решить систему из 5 уравнений
Так как в схеме 3 независимых контура, следовательно, по методу контурных токов нужно решить систему из 3 уравнений.
Так как в схеме 3 узла, следовательно, по методу узловых потенциалов нужно решить систему из 2 уравнений (3-1 = 2)
Выполним расчёт методом узловых потенциалов
комплексная амплитуда ЭДС, равна:
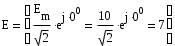
внутреннее сопротивление источника ЭДС:Rв = 500 Ом
ёмкостное сопротивление:XC2 = XC4 = XC, где

активное сопротивление:R1 = R2 = R3 = R4 = R5 = R = 100 Ом
заземлим узел «3», следовательно, его комплексный потенциал равен нулю: φ3 = 0
система уравнений в общем виде:
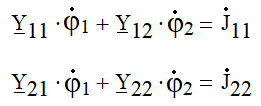
где собственные проводимости узлов, равны:

смежные проводимости между узлами (в уравнениях берутся со знаком «минус»), равны:
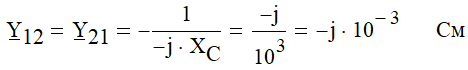
узловые токи:
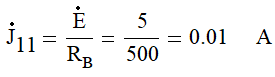
Таким образом, система уравнений имеет вид:
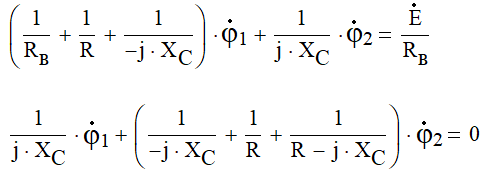
с учетом числовых данных система имеет вид:

решение системы уравнений методом Крамера:

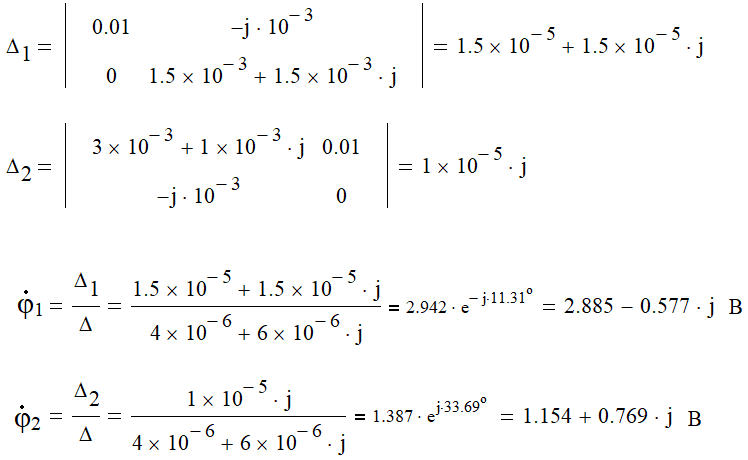
Таким образом, мы получили решение системы уравнений, потенциалы узлов: