Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx

АО, соединяющей начало координат и конец кривой, равен среднемугодовомурасходу

????_год = W_год/t_год. Аналогично, если кривая построена за несколько лет, то тангенс угла наклона этой прямой равен среднемумноголетнемурасходу.

Для того чтобы можно было находить расходы в любой момент времени или на любом интервале, не прибегая к измерению угла наклона линии к оси абсцисс, используют дополнительное построение, которое называют лучевым масштабом. Его можно строить в любом месте рядом с интегральной кривой. Часто горизонтальная ось лучевого масштаба является продолжением оси времени. На рис. 13 показано построение лучевого масштаба.

Проводят две взаимно перпендикулярные оси. Определив диапазон изменения расхода по гидрографу стока, назначают удобный масштаб расхода. Вертикальную ось (ось расходов) градуируют в выбранном масштабе. Проводят прямую, соединяющую начало координат и конец интегральной кривой (назовем ее замыкающей линией). Рассчитывают средний годовой или средний многолетний расход (в зависимости от того, за какой период построена суммарная кривая) по формуле W/t= Q_cp. Значение Q_cpоткладывают на вертикальной оси. Из точки на оси, соответствующей Q_cp, проводят линию, параллельную замыкающей, до пересечения с горизонтальной осью. Точка пересечения с осью абсцисс называется полюсом – это точка О на рис. 13. Расстояние от полюса до начала координат называют полюсным расстоянием (Р). Любой луч, проведенный

---

из полюса, будет соответствовать определенному расходу, который он отсечет на вертикальной оси. Если к заданной точке интегральной кривой провести касательную и параллельным переносом начертить эту касательную через полюс, то на вертикальной оси получим значение расхода, соответствующее тангенсу угла наклона касательной.




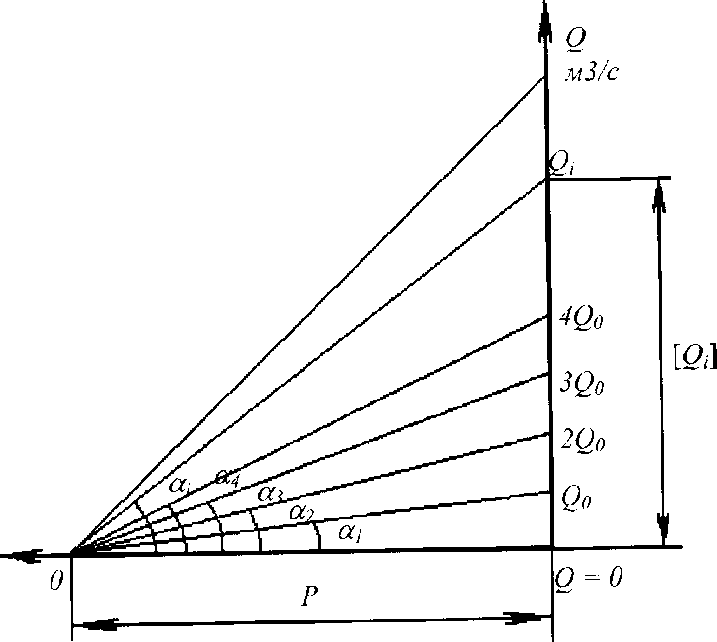
Рис. 13. Лучевой масштаб

Все расчеты по построению интегральной кривой удобно вести в табличной форме.

Как сказано выше, интегральная кривая дает возможность решать задачу о назначении объема водохранилища при полном регулировании стока. На рис. 14, а показано построение, с помощью которого определяют объем водохранилища. Если провести две касательные к интегральной кривой в крайних ее точках а и в, параллельные лучу OA, соответствующему среднему годовому расходу реки Q_cp, то расстояниеповертикалимеждуэтимикасательнымидаетполныйобъемW_вод. При этом из водохранилища можно забирать постоянный расход Q_cp.

На рисунке 14, б, впоказано, как соотносятся точки интегральной кривой с колебанием расхода воды в створе водохранилища и изменением уровня воды в самом водохранилище. До момента времени t₁ (точка а на интегральной кривой) водохранилище срабатывается (опорожняется), так как увеличивающийся расход в реке меньше Q_cp. На интервале времени t₁….t₂ приток в реке превышает Q_cp, поэтому начинается наполнение

водохранилища расходом, составляющим разность между расходом притока

---

Q_pи отдачей из него: Q= Q_p– Q_cp.

После момента времени t₂ (точка вна интегральной кривой) опять начинается сработка водохранилища из-за уменьшения притока реки. Сопоставляя рис. 14, а и б можно заметить, что в момент времени t_m, соответствующий точке перегиба на суммарной кривой, расход в реке достигает максимума (Q_max), а в момент t_n– минимума (Q_min). Колебание уровня воды в водохранилище возможно от НПУ до УМО. Таким образом, в течение года к моменту времени t₁ водохранилище срабатывается до УМО, а к моменту t₂ – наполняется до НПУ.

В качестве примера на рис. 15 приведена интегральная кривая за четырехлетний период. Тангенс угла наклона линии, соединяющей начало координат и конец суммарной кривой, равен среднему расходу за четыре года.



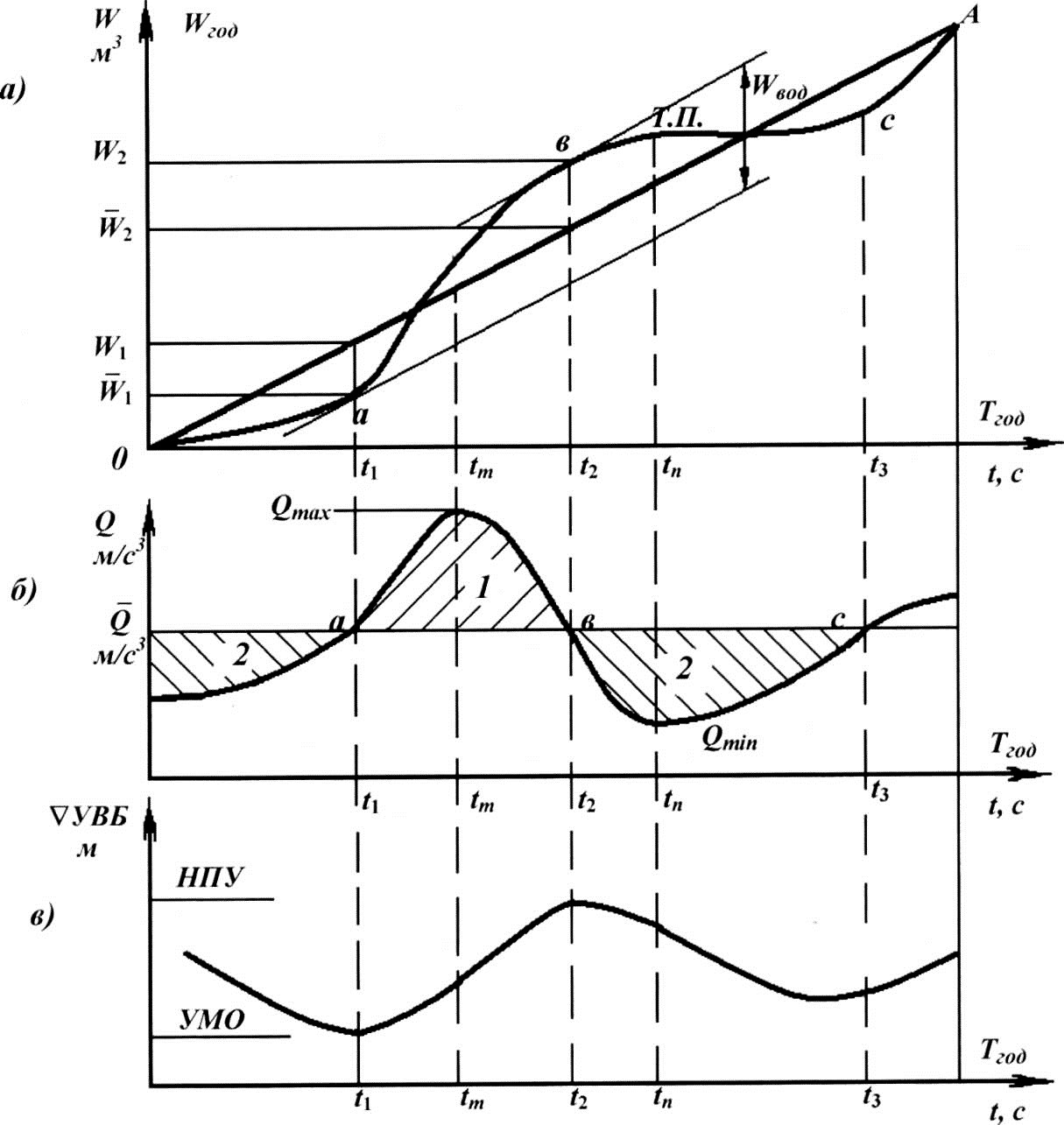
Рис. 14. Схема, иллюстрирующая взаимосвязь интегральной кривой (а), гидрографа стока (б) и колебания уровня в водохранилище (в)
Практически возможность полного регулирования стока реки часто ограничена экономическими и другими условиями. Поэтому объем водохранилища получается меньше требуемого, а во избежание переливов предусматриваются водосбросные сооружения.

При водохозяйственном расчете водохранилища на одном чертеже совмещают интегральные кривые стока W(t) и отдачи U (t). Интегральная кривая отдачи представляет собой прямую линию в случае постоянной отдачи и ломаную – при переменной отдаче. Кривые строят в одном масштабе. Сопоставляя их, находят избытки, дефициты, полезный объем и другие показатели регулирования стока.

---

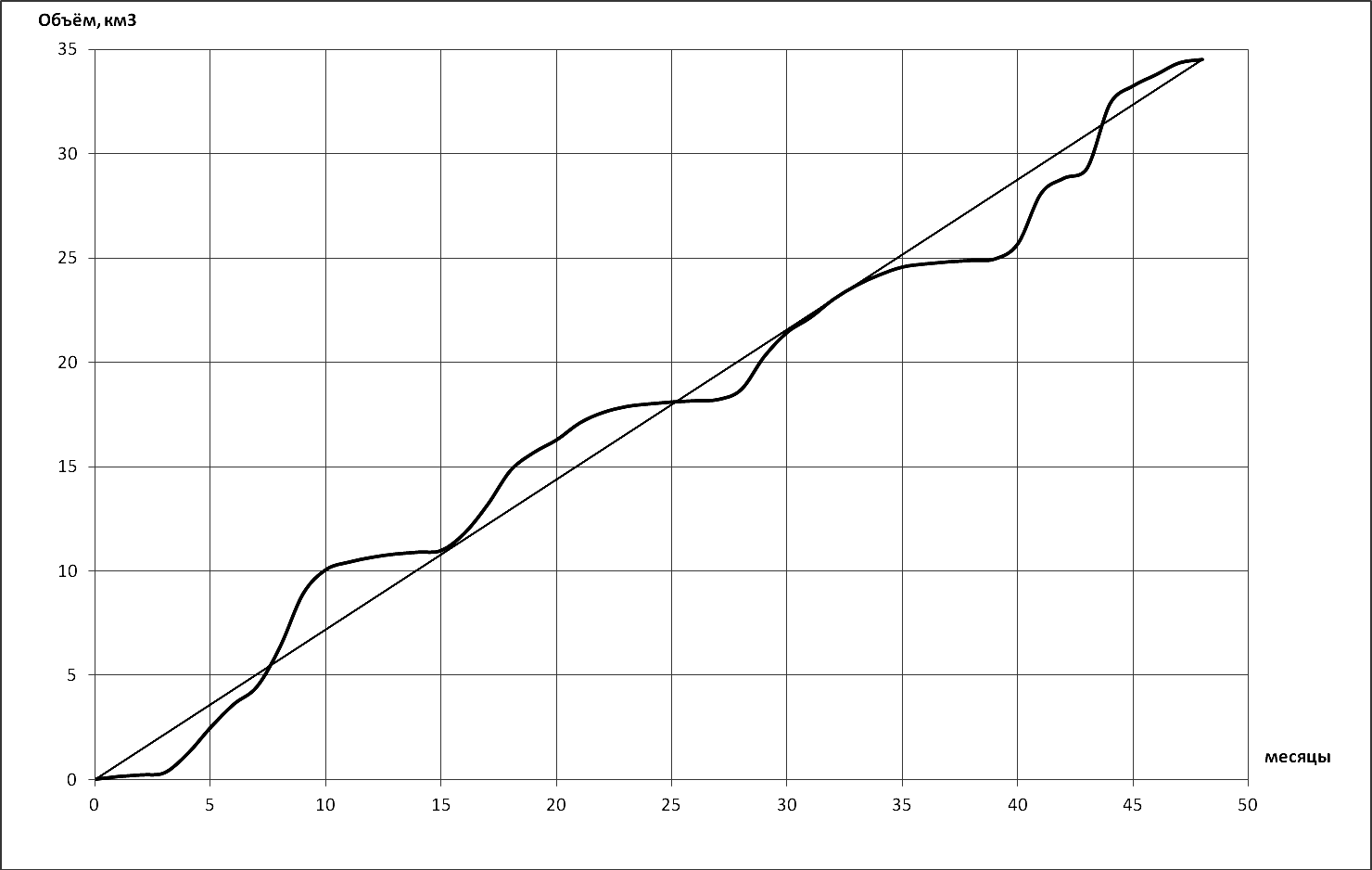
Рис. 15. Интегральная кривая за четырехлетний период

---

Пример расчета

Построить интегральную кривую стока для р. Маревки у с. Покровка (Приморский край). Исходными данными для расчета являются среднемесячные расходы реки за 4 года,

представленные в табл. 18.

Таблица 18

Среднемесячные расходы реки Маревка за период с 1963 по 1966 гг.

Годы	Расходы по месяцам года январь–декабрь, м3/с
	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
1963	1,02	0,74	2,1	46,3	38,7	16,3	7,3	45,5	106	35,5	10,2	3,7
1964	1,98	1,13	1,01	65,8	41,5	33,2	16,2	7,83	21,6	9,93	7,46	1,7
1965	1,01	0,65	0,5	29,9	47,4	13,2	6,92	19,4	23,1	14,5	16,2	1,88
1966	1,0	0,74	0,65	51,9	64,8	8,13	4,75	77,0	14,5	15,6	16,6	1,41

Учитывая, что месяцы имеют разное количество дней, необходимо рассчитать количество секунд для каждого месяца в году, чтобы определить объем стока за каждый месяц в течение

---