Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 508
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
четырех лет. Расчет приведен в табл. 19. В шестом столбце таблицы показаны объемы стока за месяц, в седьмом – объем стока, накопленный к концу каждого месяца. Например, к 30 июня 1963 г. объем стока составил 1 262,67 млн м3, а к 31 января 1964 г. – 6 263,12 млн м3. В восьмом столбце приведены значения объемов в млн м3.
Таблица 19
Расчет координат интегральной кривой стока
Интегральная кривая строится по данным столбцов 4 и 8. Для ее построения на горизонтальной оси откладывают время, а на вертикальной – объемы. Учитывая, что месяцы имеют разное количество дней, удобно за единицу измерения принять 10 суток и построение
вести в масштабе 1 см – 10 суток. Можно принять за 1 см – 30 суток, но в этом случае увеличивается погрешность при построении.
Суммарный объем, накопленный за четыре года (1461 день), составляет 2514,12 млн м3.
Рассчитывают средний многолетний расход Qcp:
????ср = ????⁄????;
????ср = 2514119040⁄(1461 ∙ 86400) = 19,9 м3/с..
На рис. 17 изображена интегральная кривая, построенная по результатам расчетов.
Чтобы пользоваться суммарной кривой, построен лучевой масштаб. На рис. 16 показано построение лучевого масштаба, по которому можно определить расход в любой точке или на любом интервале интегральной кривой. Выбран масштаб расхода (вертикальная ось): в 1 см – 5 м3/с. На шкале расходов откладывают значение рассчитанного среднего расхода Qcp= 19,9 м3/с. Из этой точки проводят линию, параллельную замыкающей линии OAинтегральной кривой (рис. 17). Эта линия пересекает горизонтальную ось лучевого масштаба в точке О(рис. 16), которая является полюсом. Величина Р– полюсное расстояние. Тангенс угла наклона замыкающей линии OAинтегральной кривой
равен среднему многолетнему расходу Qcp.
Для определения расхода в любой точке интегральной кривой проводят касательную в заданной точке и параллельно переносят её на лучевой масштаб через полюс О. На вертикальной шкале эта линия отсечет отрезок, соответствующий расходу в заданной точке.
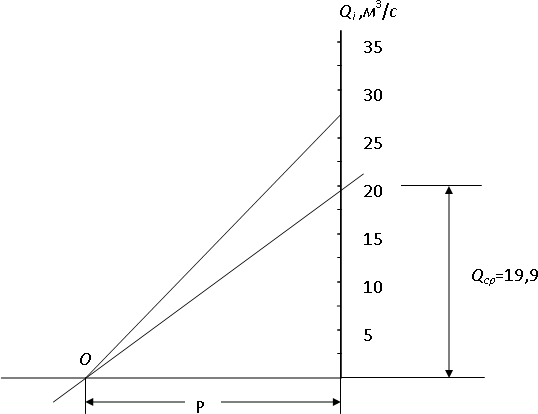 Проводя касательные или секущие интегральной кривой параллельным переносом на лучевой масштаб через точку О, получают значения расходов на вертикальной оси лучевого масштаба, отсекаемые этими параллельными. Данные расходы соответствуют выбранным моментам времени или интервалам на интегральной кривой.
Проводя касательные или секущие интегральной кривой параллельным переносом на лучевой масштаб через точку О, получают значения расходов на вертикальной оси лучевого масштаба, отсекаемые этими параллельными. Данные расходы соответствуют выбранным моментам времени или интервалам на интегральной кривой.
Рис. 16. Лучевой масштаб для определения расходов
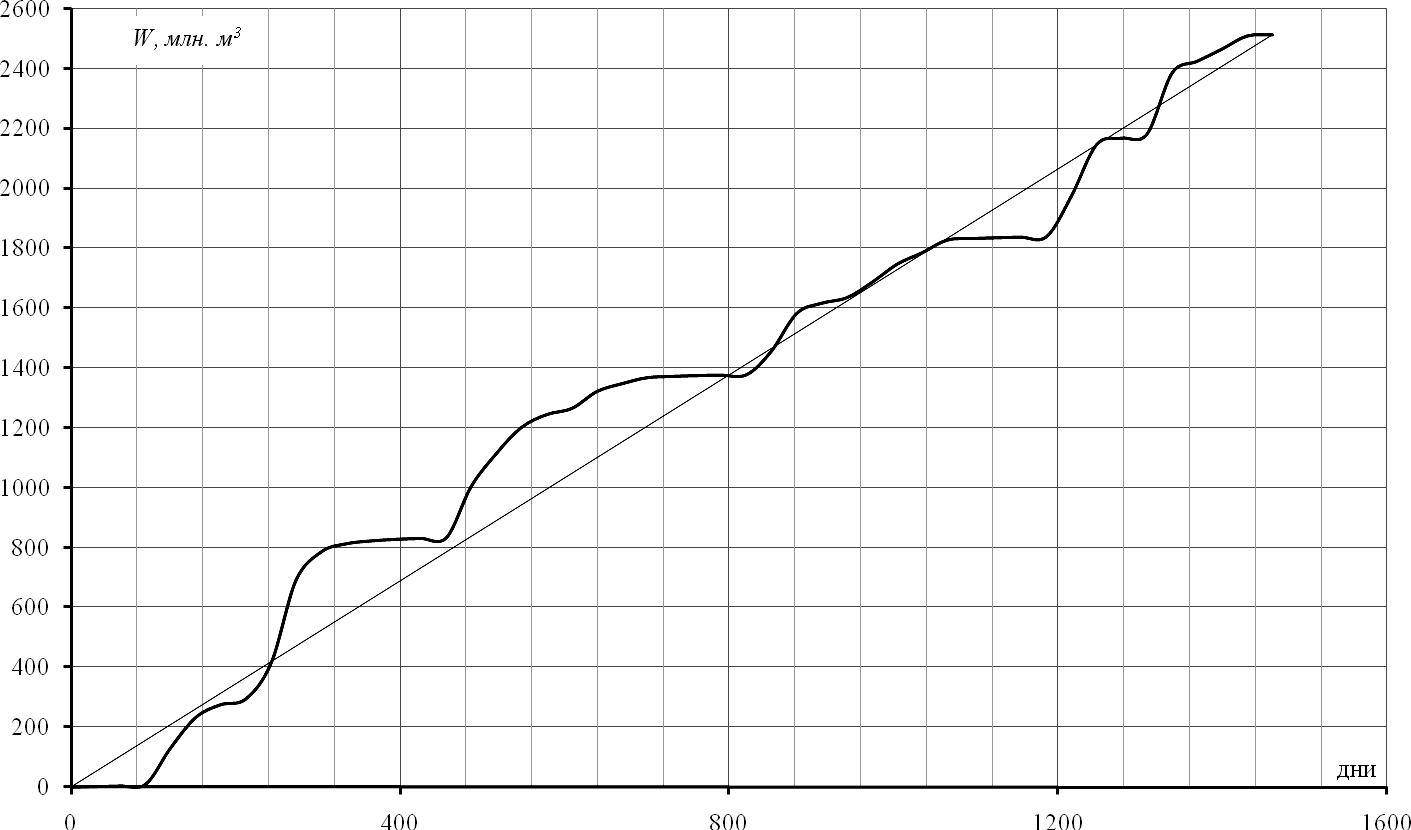
Рис. 17. Интегральная кривая стока р. Маревка за 1963–1966 гг.
СПИСОК ЛИТЕРАТУРЫ
ПРИЛОЖЕНИЕ А
Рис. А1.
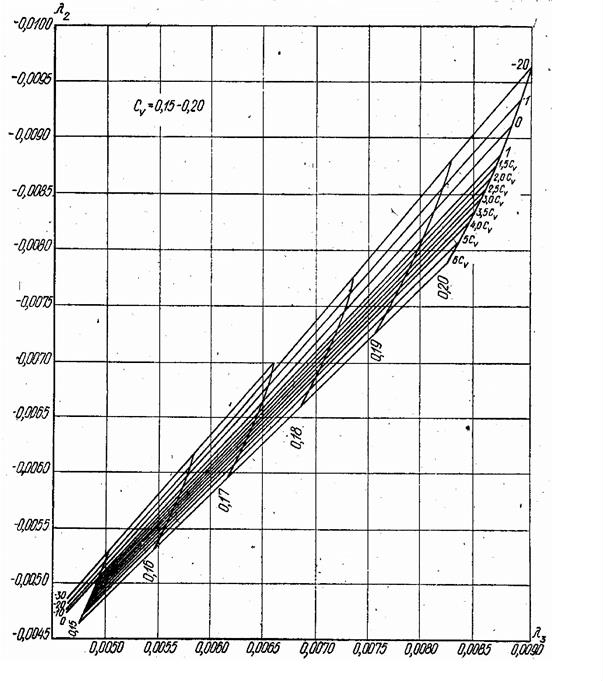 Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,15–0,20
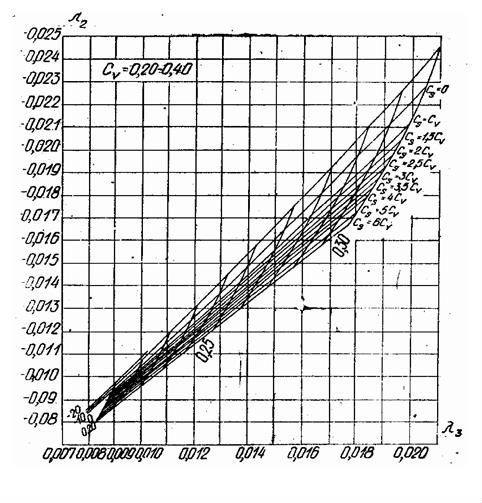
 Продолжениеприл.А
Продолжениеприл.А
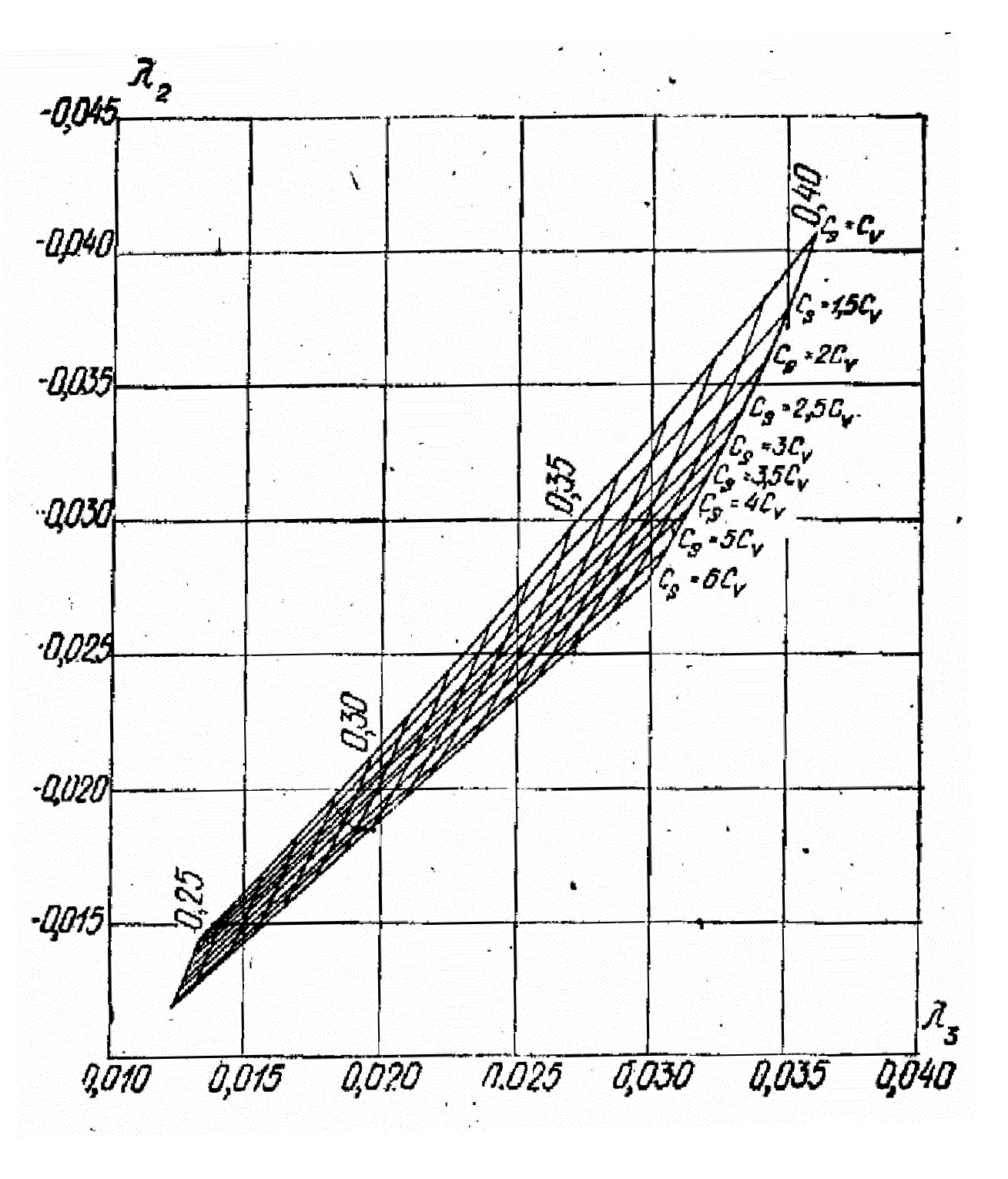
Рис. А2. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,20–0,40
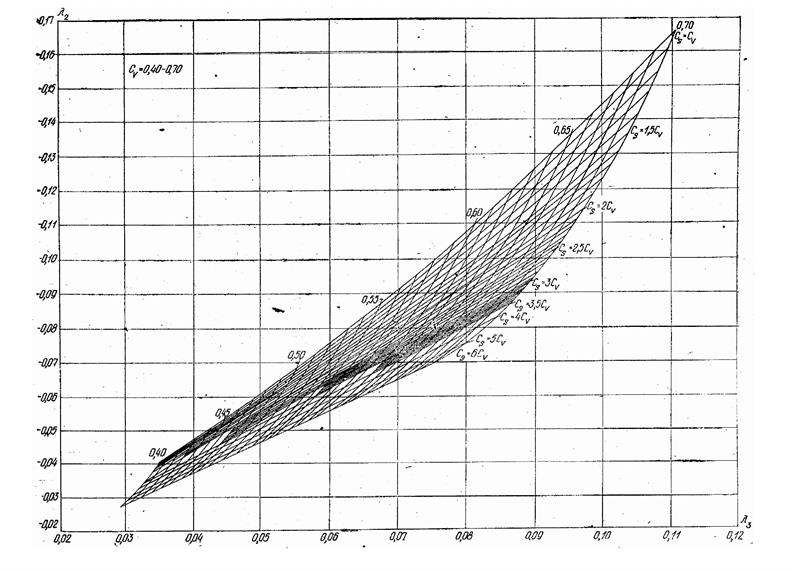
Рис. А3. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,40–0,70
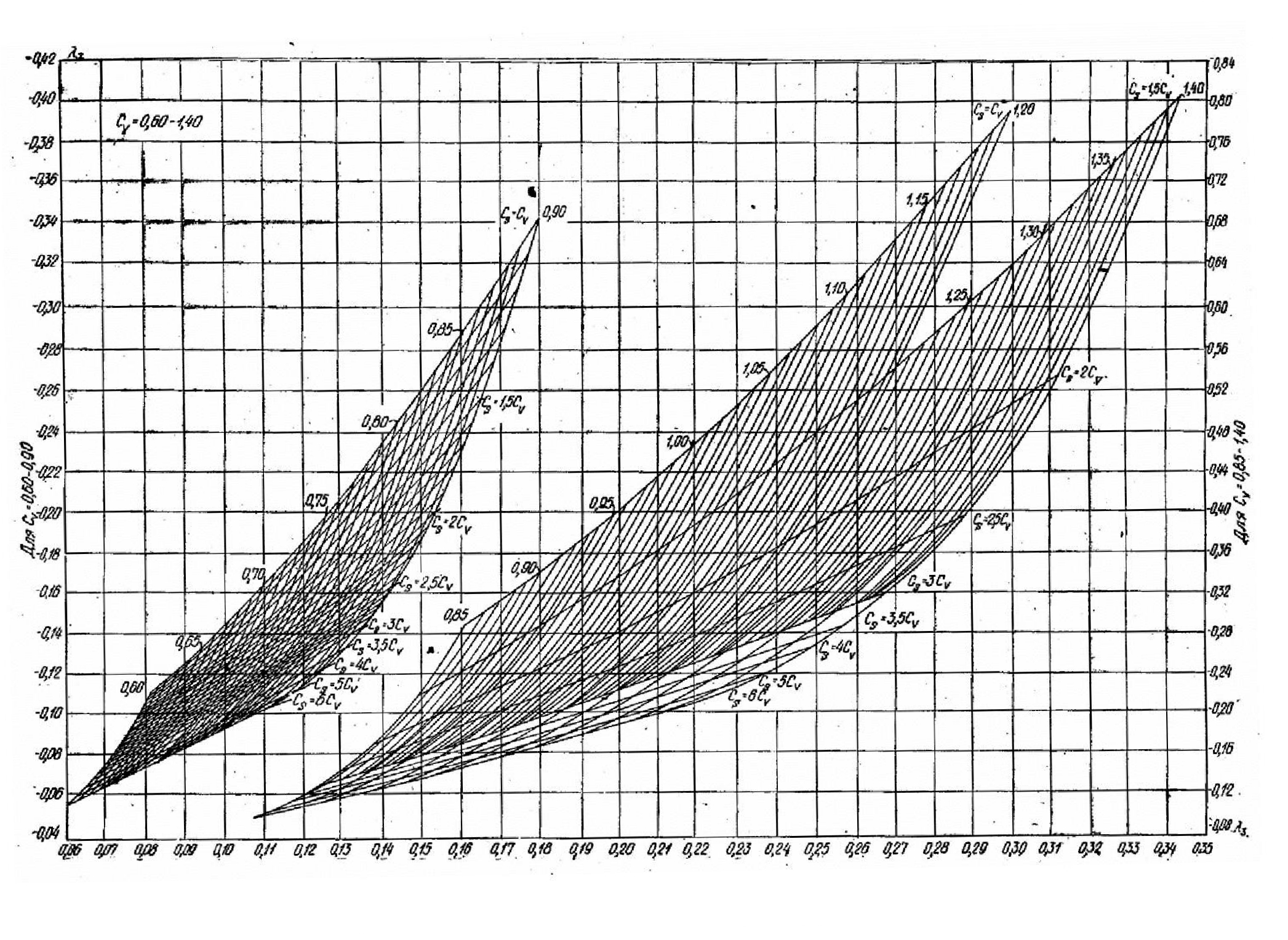
Рис. А4. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,60–1,40
ПРИЛОЖЕНИЕ Б
Таблица Б1
Таблица 19
Расчет координат интегральной кривой стока
| Год | Месяц | Кол-во дней | Q, м³/с | W= Q∙t, м³ | ΣW, м³ | ΣW, млнм³ | |
| 1963 | январь | 31 | 31 | 1,02 | 2 731 968 | 2 731 968 | 2,73 |
| февраль | 28 | 59 | 0,74 | 1 790 208 | 4 522 176 | 4,52 | |
| март | 31 | 90 | 2,1 | 5 624 640 | 10 146 816 | 10,15 | |
| апрель | 30 | 120 | 46,3 | 120 009 600 | 130 156 416 | 130,16 | |
| май | 31 | 151 | 38,7 | 103 654 080 | 233 810 496 | 233,81 | |
| июнь | 30 | 181 | 16,3 | 42 249 600 | 276 060 096 | 276,06 | |
| июль | 31 | 212 | 7,3 | 19 552 320 | 295 612 416 | 295,61 | |
| август | 31 | 243 | 45,5 | 121 867 200 | 417 479 616 | 417,48 | |
| сентябрь | 30 | 273 | 106 | 274 752 000 | 692 231 616 | 692,23 | |
| октябрь | 31 | 304 | 35,5 | 95 083 200 | 787 314 816 | 787,32 | |
| ноябрь | 30 | 334 | 10,2 | 26 438 400 | 813 753 216 | 813,75 | |
| декабрь | 31 | 365 | 3,7 | 9 910 080 | 823 663 296 | 823,66 | |
| 1964 | январь | 31 | 396 | 1,98 | 5 303 232 | 828 966 528 | 828,97 |
| февраль | 29 | 425 | 1,13 | 2 831 328 | 831 797 856 | 831,80 | |
| март | 31 | 456 | 1,01 | 2 705 184 | 834 503 040 | 834,50 | |
| апрель | 30 | 486 | 65,8 | 170 553 600 | 1 005 056 640 | 1 005,06 | |
| май | 31 | 517 | 41,5 | 111 153 600 | 1 116 210 240 | 1 116,21 | |
| Год | Месяц | Кол-во дней | Q, м³/с | W= Q∙t, м³ | ΣW, м³ | ΣW, млнм³ | |
| | июнь | 30 | 547 | 33,2 | 86 054 400 | 1 202 264 640 | 1 202,27 |
| июль | 31 | 578 | 16,2 | 43 390 080 | 1 245 654 720 | 1 245,66 | |
| август | 31 | 609 | 7,83 | 20 971 872 | 1 266 626 592 | 1 266,63 | |
| сентябрь | 30 | 639 | 21,6 | 55 987 200 | 1 322 613 792 | 1 322,62 | |
| октябрь | 31 | 670 | 9,93 | 26 596 512 | 1 349 210 304 | 1 349,21 | |
| ноябрь | 30 | 700 | 7,46 | 19 336 320 | 1 368 546 624 | 1 368,55 | |
| декабрь | 31 | 731 | 1,7 | 4 553 280 | 1 373 099 904 | 1 373,10 | |
| 1965 | январь | 31 | 762 | 1,01 | 2 705 184 | 1 375 805 088 | 1 375,81 |
| февраль | 28 | 790 | 0,65 | 1 572 480 | 1 377 377 568 | 1 377,38 | |
| март | 31 | 821 | 0,5 | 1 339 200 | 1 378 716 768 | 1 378,72 | |
| апрель | 30 | 851 | 29,9 | 77 500 800 | 1 456 217 568 | 1 456,22 | |
| май | 31 | 882 | 47,4 | 126 956 160 | 1 583 173 728 | 1 583,18 | |
| июнь | 30 | 912 | 13,2 | 34 214 400 | 1 617 388 128 | 1 617,39 | |
| июль | 31 | 943 | 6,92 | 18 534 528 | 1 635 922 656 | 1 635,92 | |
| август | 31 | 974 | 19,4 | 51 960 960 | 1 687 883 616 | 1 687,89 | |
| сентябрь | 30 | 1004 | 23,1 | 59 875 200 | 1 747 758 816 | 1 747,76 | |
| октябрь | 31 | 1035 | 14,5 | 38 836 800 | 1 786 595 616 | 1 786,60 | |
| ноябрь | 30 | 1065 | 16,2 | 41 990 400 | 1 828 586 016 | 1 828,59 | |
| декабрь | 31 | 1096 | 1,88 | 5 035 392 | 1 833 621 408 | 1 833,62 | |
| 1966 | январь | 31 | 1127 | 1 | 2 678 400 | 1 836 299 808 | 1 836,30 |
| февраль | 28 | 1155 | 0,74 | 1 790 208 | 1 838 090 016 | 1 838,09 | |
| март | 31 | 1186 | 0,65 | 1 740 960 | 1 839 830 976 | 1 839,83 | |
| апрель | 30 | 1216 | 51,9 | 134 524 800 | 1 974 355 776 | 1 974,36 | |
| май | 31 | 1247 | 64,8 | 173 560 320 | 2 147 916 096 | 2 147,92 | |
| июнь | 30 | 1277 | 8,13 | 21 072 960 | 2 168 989 056 | 2 168,99 | |
| июль | 31 | 1308 | 4,75 | 12 722 400 | 2 181 711 456 | 2 181,71 | |
| август | 31 | 1339 | 77 | 206 236 800 | 2 387 948 256 | 2 387,95 | |
| сентябрь | 30 | 1369 | 14,5 | 37 584 000 | 2 425 532 256 | 2 425,53 | |
| октябрь | 31 | 1400 | 15,6 | 41 783 040 | 2 467 315 296 | 2 467,32 | |
| ноябрь | 30 | 1430 | 16,6 | 43 027 200 | 2 510 342 496 | 2 510,34 | |
| декабрь | 31 | 1461 | 1,41 | 3 776 544 | 2 514 119 040 | 2 514,12 | |
Интегральная кривая строится по данным столбцов 4 и 8. Для ее построения на горизонтальной оси откладывают время, а на вертикальной – объемы. Учитывая, что месяцы имеют разное количество дней, удобно за единицу измерения принять 10 суток и построение
вести в масштабе 1 см – 10 суток. Можно принять за 1 см – 30 суток, но в этом случае увеличивается погрешность при построении.
Суммарный объем, накопленный за четыре года (1461 день), составляет 2514,12 млн м3.
Рассчитывают средний многолетний расход Qcp:
????ср = ????⁄????;
????ср = 2514119040⁄(1461 ∙ 86400) = 19,9 м3/с..
На рис. 17 изображена интегральная кривая, построенная по результатам расчетов.
Чтобы пользоваться суммарной кривой, построен лучевой масштаб. На рис. 16 показано построение лучевого масштаба, по которому можно определить расход в любой точке или на любом интервале интегральной кривой. Выбран масштаб расхода (вертикальная ось): в 1 см – 5 м3/с. На шкале расходов откладывают значение рассчитанного среднего расхода Qcp= 19,9 м3/с. Из этой точки проводят линию, параллельную замыкающей линии OAинтегральной кривой (рис. 17). Эта линия пересекает горизонтальную ось лучевого масштаба в точке О(рис. 16), которая является полюсом. Величина Р– полюсное расстояние. Тангенс угла наклона замыкающей линии OAинтегральной кривой
равен среднему многолетнему расходу Qcp.
Для определения расхода в любой точке интегральной кривой проводят касательную в заданной точке и параллельно переносят её на лучевой масштаб через полюс О. На вертикальной шкале эта линия отсечет отрезок, соответствующий расходу в заданной точке.
 Проводя касательные или секущие интегральной кривой параллельным переносом на лучевой масштаб через точку О, получают значения расходов на вертикальной оси лучевого масштаба, отсекаемые этими параллельными. Данные расходы соответствуют выбранным моментам времени или интервалам на интегральной кривой.
Проводя касательные или секущие интегральной кривой параллельным переносом на лучевой масштаб через точку О, получают значения расходов на вертикальной оси лучевого масштаба, отсекаемые этими параллельными. Данные расходы соответствуют выбранным моментам времени или интервалам на интегральной кривой.Рис. 16. Лучевой масштаб для определения расходов

Рис. 17. Интегральная кривая стока р. Маревка за 1963–1966 гг.
СПИСОК ЛИТЕРАТУРЫ
-
Орлов В.Г., Сикан А.В. Основы инженерной гидрологии. М.: Изд-во РГГМУ, 2003. -
Михайлов В.Н., Добровольский А.Д., Добролюбов С.А. Гидрология: учебник для вузов. М.: Высш. шк., 2007. -
Канарский Н.Д. Михалев М.А. Гидрологические расчеты: учеб. пособие. Л.: ЛПИ имени М.И. Калинина, 1977. -
Железняков Г.В., Неговская Т.А., Овчаров Е.Е. Гидрология, гидрометрия и регулирование стока / под ред. Г.В. Железнякова. М.: Колос, 1984. -
СП 33-101-2003. Определение основных расчетных гидрологических характеристик / Госстрой России. -
СП 58.13330.2012. Гидротехнические сооружения. Основные положения. Актуализированная редакция СНиП 33-01-2003 (с Изменением № 1). -
СП 31.13330.2012. Водоснабжение. Наружные сети и сооружения. Актуализированная редакция СНиП 2.04.02-84 (с Изменениями № 1, 2). -
Гидрологический ежегодник 1976 г. Т. 9. Бассейн Тихого океана. Вып. 6. Бассейн р. Уссури и бассейн Японского моря, 1977. -
ГОСТ 19179-73. Гидрология суши. Термины и определения.
ПРИЛОЖЕНИЕ А
Рис. А1.
 Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Csметодом наибольшего вероятного правдоподобия при Cv= 0,15–0,20

 Продолжениеприл.А
Продолжениеприл.АРис. А2. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,20–0,40

Рис. А3. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,40–0,70

Рис. А4. Номограммы для вычисления параметров трехпараметрического гамма-распределения Cvи Cs
методом наибольшего вероятного правдоподобия при Cv= 0,60–1,40
ПРИЛОЖЕНИЕ Б
Таблица Б1