Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 504
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
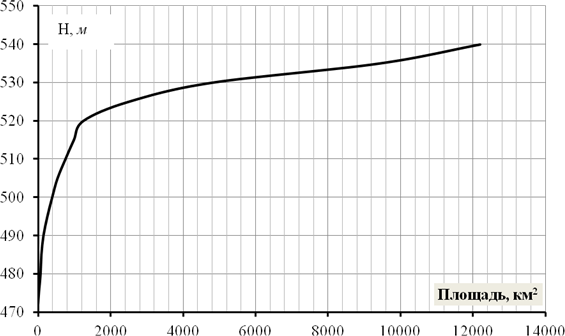
Рис. 9. Кривая площадей – зависимость
f(H)
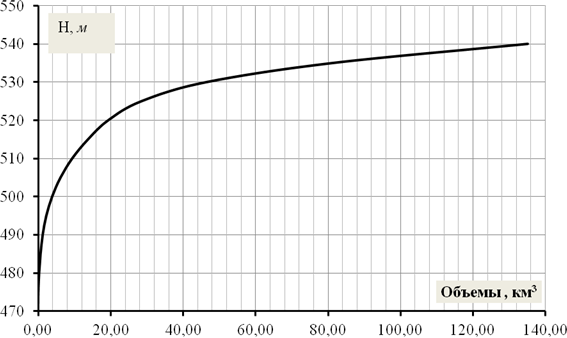
Рис. 10. Кривая объемов – зависимость V
f(H)
Кривые площадей и объемов строят на одном графике с общей осью ординат H. Горизонтальный масштаб выбирается для каждой кривой по его максимальному значению.
- 1 ... 10 11 12 13 14 15 16 17 ... 21
ПОСТРОЕНИЕ ИНТЕГРАЛЬНОЙ (СУММАРНОЙ) КРИВОЙ СТОКА
Для выполнения ряда инженерных расчетов важной характеристикой реки является гидрограф стока, показывающий изменение расхода Q воды в течение времени в конкретном створе реки. Гидрограф стока содержит исходные данные для построения интегральной (суммарной) кривой стока, которая показывает последовательное накопление стока воды в рассматриваемом створе реки за определенный период времени.
Интегральные кривые стока могут быть построены в прямоугольных и косоугольных координатах. В прямоугольных координатах, как правило, строят за небольшой период (сутки, неделю, сезон года, год), так как при расчетном периоде, равном нескольким годам, масштаб объемов может оказаться слишком мелким, что снизит точность расчетов.
Интегральная кривая используется при графических расчетах регулирования стока. В частности, она дает возможность решить задачу о назначении объема водохранилища в случае полного регулирования стока реки. Если построить суммарную кривую притока и требуемой отдачи воды в створе проектируемого водохранилища, то можно получить разностную интегральную кривую, которую называют еще интегральной кривой в косоугольной системе координат.
Расчет интегральной кривой стока заключается в определении объема стока Wiза малые интервалы времени tiсо средним расходом на интервале Qi. На рис. 11, а показан гидрограф стока в виде столбчатой гистограммы со средними расходами на интервалах. Объем стока определяется при этом методом графического интегрирования
(методом прямоугольников):
Wi Qi ti. (31)
Для нахождения суммарного стока, накопившегося к любому моменту времени, эти объемы суммируют.
n
Wi Wi
i1
. (32)
Чем меньше расчетный интервал времени, тем точнее полученный результат. Если tiравно одному месяцу, то Qi– это среднемесячный расход, а п – число месяцев в расчетном периоде. Если tiравно одному дню, то Qi– среднесуточный расход, а п – число дней в расчетном периоде. На рис. 11 приведен участок гидрографа стока (а) и соответствующий ему отрезок интегральной кривой (б).
Расчетный интервал времени от 0 до tkразбит на интервалы ti. Конец каждого интервала соответствует времени ti. Например, если tiравно одному месяцу, то t1 – январь,
t2 – февраль, t3 – март, t4 – апрель и т.д., a t1 – конец первого интервала (31 января), t2 – конец второго интервала (28 февраля), t3 – третьего (31 марта) и т.д. Расход Q1 – это среднемесячный расход на первом интервале (за январь), Q2 – среднемесячный расход на втором интервале (за февраль), Q3 – на третьем (за март) и т.д. Таким образом, по формуле
-
находят объемы стока на каждом интервале (за каждый месяц), а по формуле (32) определяют объемы стока, накопленные к концу каждого интервала (путем суммирования предыдущих).
По координатам «время» – «объем стока» строят интегральную кривую (Wi=f(t)).
Надо отметить,
что во всех расчетах время должно быть выражено в секундах, так как расходы измеряются в м3/с.
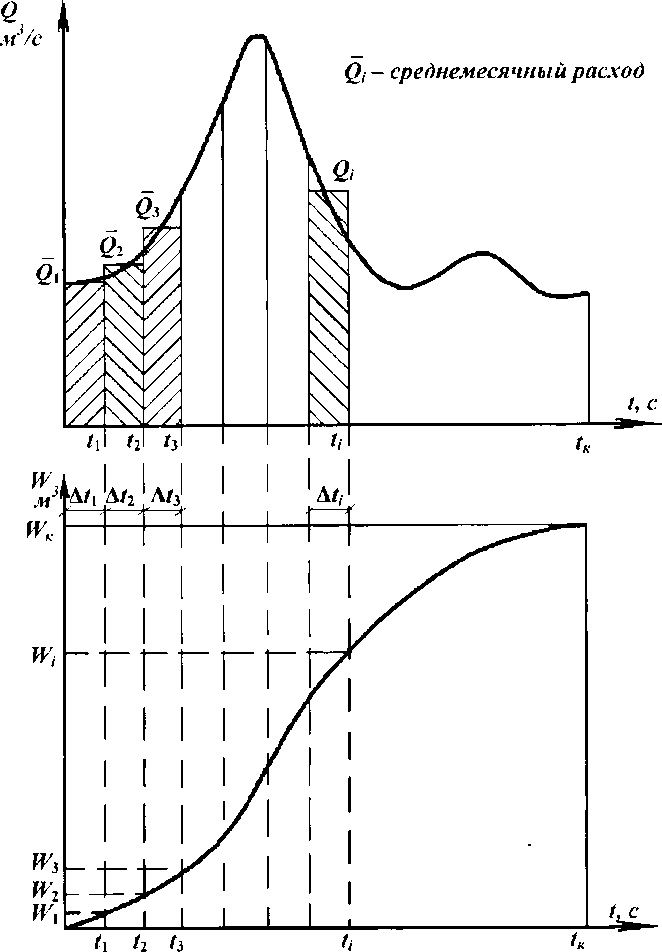 а)
а)б)
Рис. 11. Пример построения интегральной кривой по гидрографу стока методом графического интегрирования
Анализируя интегральную кривую, можно выявить ряд свойств этой кривой.
-
Функция W= f(t)является неубывающей.Поскольку это суммарная кривая, то накопленный сток не может уменьшаться, он возрастает и при нарастании расхода, и при его убывании. А в случае отсутствия стока (перемерзание или пересыхание реки) накопленное значение объема стока остается постоянным и графически представляется в виде прямой, параллельной оси времени. -
Точки перегиба на суммарной кривой соответствуют максимальному (Qmax) или минимальному(Qmin) расходунагидрографестока. Точкой перегиба графика некоторой функции y = f(x) называется точка, в которой меняется направление выпуклости графика. Если до точки перегиба интегральная кривая обращена выпуклостью вниз, то вторая производная объема по времени d2W/dt2 (или производная расхода по времени dQ/dt) – функция положительная, т.е. расход возрастает. После точки перегиба кривая обращена выпуклостью вверх, и вторая производная объема по времени (или производная расхода по времени) – функция отрицательная, т.е. расход убывает. Производная dQ/dt в точке перегиба интегральной кривой меняет свой знак с «+» на «–», значит, точке перегиба соответствует максимум расхода на гидрографе стока. Аналогичными рассуждениями можно показать, что
точке интегральной кривой, где происходит смена выпуклого участка на вогнутый, соответствует минимум расхода на гидрографе стока.
-
Тангенсугланаклоналинии, соединяющей две точки на интегральной кривой, равен среднему расходу на выбранном интервале. На рис. 12 приведена иллюстрация этого свойства суммарной кривой. Через точки 1 и 2, соответствующие моментам времени t1 и t2, проведена линия. Объем стока ко времени t1 составил W1, а ко времени t2 – W2. За время t1-2
= t2 – t1 объем изменился на W1-2 = W2 – W1. Отношение объема ко времени W1-2/t1-2 дает,
 с одной стороны, средний расход ????1−2 за время t1-2, с другой – является тангенсом угла наклона линии, соединяющей точки 1 и 2, tg1.
с одной стороны, средний расход ????1−2 за время t1-2, с другой – является тангенсом угла наклона линии, соединяющей точки 1 и 2, tg1.-
Тангенсугланаклонакасательнойк интегральной кривой равенрасходуQiвданныймоментвремени. Для иллюстрации этого свойства воспользуемся тем же рис. 12. При сокращении расстояния между точками 1 и 2 интервал времени сокращается и в пределе стремится к нулю t 0. А линия, соединяющая точки 1 и 2, обращается в касательную в точке 2, имеющую угол наклона к оси абсцисс 2.
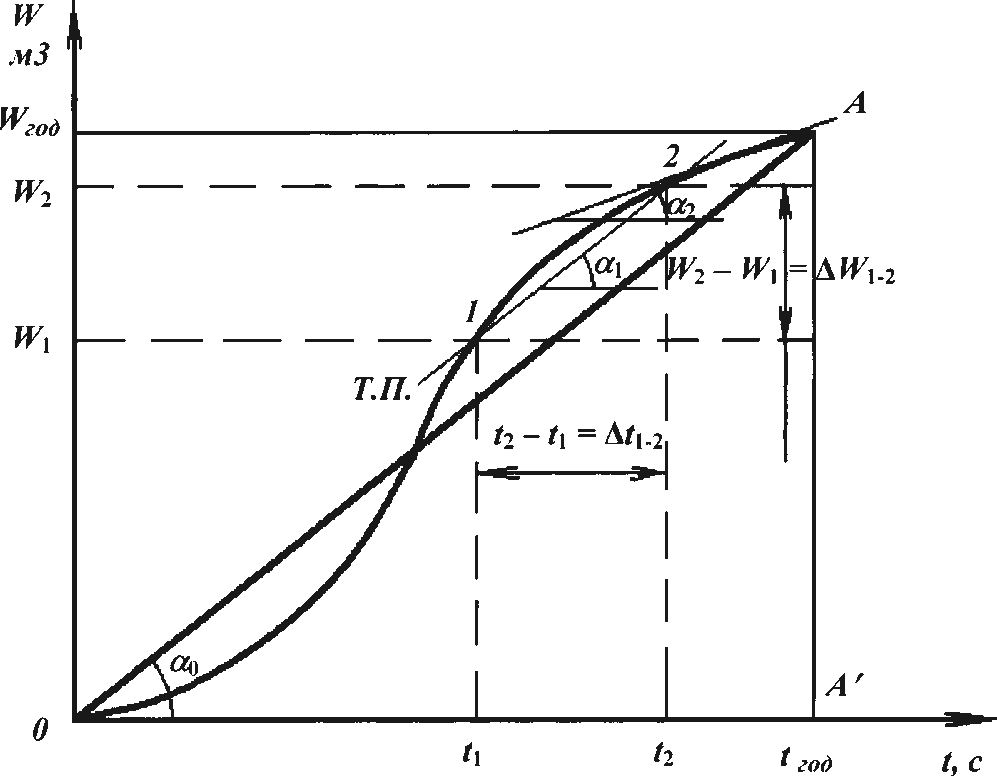 lim(W/t) = dW/dt= tg2 = Q2.
lim(W/t) = dW/dt= tg2 = Q2.Рис. 12. Схема к анализу интегральной кривой
-
Если интегральная кривая построена за один год, то тангенсугланаклонапрямой