Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 485
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
В данном случае значение Csлежит между Cs= 2,5Cvи Cs= 3,0Cv. Выбирают большее из полученных, т.е. принимают Cs= 3,0Cv.
Далее обращаются к таблице модульных коэффициентов при Cs= 3,0Cv(прил. Б, табл. Б5) и для значения Cv= 0,49 выписывают значения модульных коэффициентов kрпри разных величинах обеспеченности. В таблице даны значения kрпри Cv= 0,4 и Cv= 0,5. Методом интерполяции определяют все коэффициенты kрдля Cv= 0,49. Расчет этих коэффициентов приведен в табл. 8, а теоретическая кривая обеспеченности показана на рис. 4.
По заданию необходимо определить расход 1% обеспеченности. При Cv= 0,4: k1% = 2,25; при Cv= 0,5: k1% = 2,66. Методом интерполяции определяют модульный коэффициент при Cv= 0,49: k1% = 2,62. Расход 1% обеспеченности рассчитывают по формуле (8):
Q1% = 2,62 234 = 613 м3/с.
Расчет статистик 2
и 3
Таблица 7
| Q | Ki= Qi/Q0 | LgKi | KiLgKi |
| 514 | 2,195549 | 0,341543 | 0,749875 |
| 480 | 2,050318 | 0,311821 | 0,639333 |
| 380 | 1,623169 | 0,210364 | 0,341456 |
| 350 | 1,495024 | 0,174648 | 0,261103 |
| 346 | 1,477938 | 0,169656 | 0,250741 |
| 325 | 1,388236 | 0,142463 | 0,197773 |
| 312 | 1,332707 | 0,124735 | 0,166235 |
| 312 | 1,332707 | 0,124735 | 0,166235 |
| 295 | 1,260091 | 0,100402 | 0,126516 |
| 290 | 1,238734 | 0,092978 | 0,115175 |
| 280 | 1,196019 | 0,077738 | 0,092976 |
| 276 | 1,178933 | 0,071489 | 0,084281 |
| 255 | 1,089232 | 0,03712 | 0,040433 |
| 250 | 1,067874 | 0,02852 | 0,030456 |
| 215 | 0,918372 | -0,03698 | -0,03396 |
| 208 | 0,888471 | -0,05136 | -0,04563 |
| 203 | 0,867114 | -0,06192 | -0,0537 |
| 196 | 0,837213 | -0,07716 | -0,0646 |
| 185 | 0,790227 | -0,10225 | -0,0808 |
| 155 | 0,662082 | -0,17909 | -0,11857 |
| 154 | 0,65781 | -0,1819 | -0,11966 |
| 152 | 0,649267 | -0,18758 | -0,12179 |
| 147 | 0,62791 | -0,2021 | -0,1269 |
| 120 | 0,51258 | -0,29024 | -0,14877 |
| 118 | 0,504037 | -0,29754 | -0,14997 |
| 110 | 0,469865 | -0,32803 | -0,15413 |
| 106 | 0,452779 | -0,34411 | -0,15581 |
| 104 | 0,444236 | -0,35239 | -0,15654 |
| 98,6 | 0,42117 | -0,37554 | -0,15817 |
| 86,8 | 0,370766 | -0,4309 | -0,15976 |
| | | = –1,49088 | = 1,413832 |
На построенную теоретическую кривую обеспеченности (рис. 4) накладывают точки эмпирической кривой, координаты которой рассчитаны в табл. 6 и приведены на рис. 3. Это позволяет оценить правильность построения теоретической кривой обеспеченности:
полученная теоретическая кривая на большей ее части должна проходить близко к эмпирическим значениям координат. Большие отклонения свидетельствуют о неправильном подборе теоретической кривой.
Таблица 8
Расчет значений модульных коэффициентов
| P,% | При Сv = 0,4 | При Сv = 0,5 | При Сv = 0,49 |
| 0,001 | 4,69 | 6,3 | 6,14 |
| 0,01 | 3,78 | 5 | 4,88 |
| 0,03 | 3,41 | 4,34 | 4,25 |
| 0,05 | 3,23 | 4,1 | 4,01 |
| 0,1 | 3 | 3,75 | 3,68 |
| 0,3 | 2,64 | 3,22 | 3,16 |
| 0,5 | 2,48 | 3 | 2,95 |
| 1 | 2,25 | 2,66 | 2,62 |
| 3 | 1,91 | 2,17 | 2,14 |
| 5 | 1,75 | 1,94 | 1,92 |
| 10 | 1,52 | 1,63 | 1,62 |
| 20 | 1,29 | 1,33 | 1,33 |
| 25 | 1,21 | 1,23 | 1,23 |
| 30 | 1,14 | 1,15 | 1,15 |
| 40 | 1,03 | 1,01 | 1,01 |
| 50 | 0,93 | 0,9 | 0,90 |
| 60 | 0,84 | 0,79 | 0,80 |
| 70 | 0,76 | 0,7 | 0,71 |
| 75 | 0,72 | 0,65 | 0,66 |
| 80 | 0,67 | 0,6 | 0,61 |
| 90 | 0,57 | 0,48 | 0,49 |
| 95 | 0,49 | 0,41 | 0,42 |
| 97 | 0,45 | 0,36 | 0,37 |
| 99 | 0,37 | 0,29 | 0,30 |
| 99,5 | 0,34 | 0,25 | 0,26 |
| 99,7 | 0,31 | 0,23 | 0,24 |
| 99,9 | 0,27 | 0,19 | 0,20 |
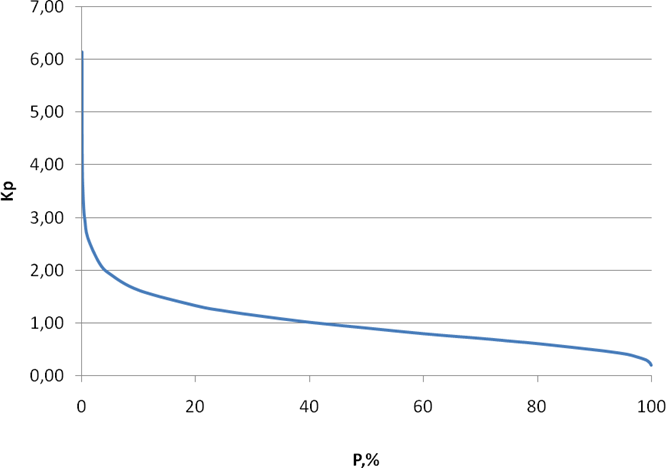
Рис. 4. Теоретическая кривая обеспеченности
- 1 ... 4 5 6 7 8 9 10 11 ... 21
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
Происходящие в природе явления настолько сложны и многообразны, что полный учет всех факторов, влияющих на эти явления, оказывается затруднительным. Например, расход весеннего половодья зависит не только от мощности снежного покрова, но и от количества весенних осадков, скорости нарастания положительных температур, предварительного увлажнения почвы и других факторов. В связи с невозможностью учета всех этих факторов зависимость между максимальным расходом половодья и мощностью снежного покрова имеет приближенный характер.
Если некоторая функция у зависит не только от переменных x1, х2... хn, но и от других причин, то связь между уи x1, х2... хnназывается неточной, или корреляционной.
При наличии корреляционной зависимости каждому значению аргумента может соответствовать несколько значений функции.
При функциональной зависимости каждому значению аргумента соответствует одно, вполне определенное значение функции. К функциональным зависимостям относятся все законы физики, химии и т. д.
Корреляционную зависимость можно выразить аналитически, т.е. подобрать уравнения, связывающие х и у корреляционно. Такие уравнения называются уравнениями регрессии.
Прямая, проведенная так, что сумма квадратов отклонений от нее ординат уотдельных точек наименьшая, даст наиболее вероятные значения у при заданном х. Эта прямая называется линией регрессии у по х.
Прямая, проведенная так, что сумма
квадратов отклонений от нее абсцисс xотдельных точек наименьшая, даст наиболее вероятные значения х при заданном у. Эта прямая называется линией регрессии х по у.
Мерой тесноты связи между рассматриваемыми величинами служит коэффициент корреляции, выражаемый формулой:
yiy0xix0
 r
r , (13)
где х0 и у0 – среднеарифметические значения членов каждого ряда; хiи уi– соответственно, наблюденные значения рассматриваемых характеристик.
Если вести обозначение хi= хi– х0 и уi= уi– у0, то выражение (13) примет вид:
xiyi
i
i
 r
r x2 y2
. (14)
Значения r колеблются от –1 до +1. Чем ближе к единице, тем теснее связь между рассматриваемыми величинами. В пределе, при r = ± 1, связь становится функциональной. В гидрологических расчетах зависимости считают удовлетворительными, если коэффициент корреляции rмежду стоком в приводимом пункте и пункте-аналоге не менее 0,7 [5]. Коэффициент корреляции может быть отрицательным – это показатель обратной зависимости между рассматриваемыми параметрами. Следует отметить, что при выборе рек-