Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 487
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
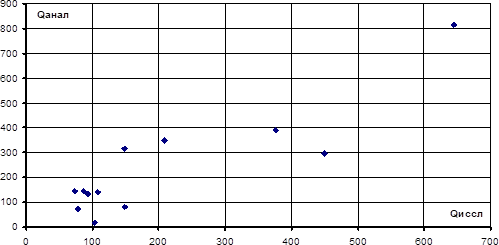
Предварительно выполняется графическая оценка. Для этого надо нанести значения расходов двух рек из табл. 10 на график связи Qи и Qa, как показано на рис. 6. Всего выбрано 12 точек. Это годы, в которых есть данные наблюдений на обеих реках: в 1950 г., и с 1958 по 1968 гг.
По рассеянию точек на графике видно, что существует связь между точками и она имеет линейный корреляционный характер. Сильно отклоняющихся точек нет, поэтому можно выполнять расчет коэффициента корреляции.
По рассчитанному уравнению регрессии можно будет удлинить ряд значений расходов исследуемой реки до 1940 г.
 м3/с
м3/см3/с
Рис. 6. Графическая интерпретация связи расходов двух рек
Расчет выполняется в табличной форме по образцу табл. 9. Предварительно
????=1
определим Х0 и Y0. Для этого просуммируем значения расходов на исследуемой реке ∑12
????????,и
????=1
и значения расходов на реке-аналоге ∑12 ????????,а, затем разделим на количество лет совместных
наблюдений:
12
Х0 = Qi,и/12 = 209,858, м3/с;
i1
12
Y0 = Qi,а/12= 242,258, м3/с.
i1
Остальные расчеты приведены в табл. 11.
При расчетах ∑ ???????? и ∑ ???????? должны стремиться к нулю. В данном случае расчет выполнялся с точностью до 0,001, поэтому суммы практически равны нулю.
После выполнения проверки по столбцам 3 и 4 производится дальнейший расчет с построчной проверкой, как указано в примечании к табл. 9. Например,
(434,142 + 570,742)2 = 188478,99 + 2 247782,738 + 325746,05
1009791,514 = 1009791,514.
После заполнения таблицы выполняется контроль сумм в последней строке.
Совпадение результатов говорит о правильности вычислений.
Далее рассчитывают коэффициент корреляции rпо формуле (14):
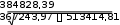 r 0,886 .
r 0,886 .Достоверность (неслучайность) значения коэффициента корреляции rоценивается по формуле (15):
 0,886 12 1
0,886 12 1
KД
13,7 .
1 0,8862
Таблица 11
Расчет коэффициента корреляции
| Хi | Yi | ∆xi | ∆yi | ∆xi∙∆yi | ∆xi² | ∆yi² | (∆xi∙∆yi)² |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 644 | 813 | 434,142 | 570,742 | 247782,738 | 188478,99 | 325746,05 | 1009790,514 |
| 78,5 | 75,5 | -131,36 | -166,76 | 21905,097 | 17255,012 | 27808,342 | 88873,547 |
| 86,6 | 145 | -123,26 | -97,258 | 11987,900 | 15192,617 | 9459,1834 | 48627,600 |
| 108 | 140 | -101,86 | -102,26 | 10415,863 | 10375,12 | 10456,767 | 41663,614 |
| 73,4 | 145 | -136,46 | -97,258 | 13271,710 | 18620,877 | 9459,1834 | 54623,480 |
| 449 | 296 | 239,142 | 53,7417 | 12851,872 | 57188,737 | 2888,1667 | 85780,647 |
| 92,8 | 135 | -117,06 | -107,26 | 12555,482 | 13702,653 | 11504,35 | 50317,967 |
| 209 | 350 | -0,8583 | 107,742 | -92,478 | 0,7367361 | 11608,267 | 11424,047 |
| 149 | 317 | -60,858 | 74,7417 | -4548,653 | 3703,7367 | 5586,3167 | 192,747 |
| 149 | 81 | -60,858 | -161,26 | 9813,913 | 3703,7367 | 26004,25 | 49335,814 |
| 103 | 17,6 | -106,86 | -224,66 | 24006,615 | 11418,703 | 50471,367 | 109903,300 |
| 376 | 392 | 166,142 | 149,742 | 24878,330 | 27603,053 | 22422,567 | 99782,280 |
| Сумма | хi = 0 | yi = 0 | 384828,389 | 367243,97 | 513414,81 | 1650315,557 | |
При Кд = 13,7 коэффициент корреляции считается достоверным. Вероятная
погрешностькоэффициента корреляции rоценивается по формуле (20):
0,674 (1 r2 )
 Er
Er ; (20)
 Er
Er 0,674 (1 0,8862 )
0,042 .
Чем меньше погрешность, тем надежнее полученное значение r.
Таким образом, значение коэффициента корреляции r= 0,886 ± 0,042, что свидетельствует о достаточно тесной связи между расходами двух рассматриваемых рек: исследуемой реки и реки-аналога (r > 0,7).
Для составления уравнений регрессии необходимо рассчитать средние квадратические отклонения расходов по формулам (18) и (19):
x
y
182,718 ;
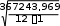
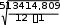 216,042 .
216,042 .Уравнения регрессии составляются по формулам (16) и (17) с учетом полученных выше значений х, y и r:
182,718
x 209,858 0,886 182,718 y 242,258.
216,042
После преобразований получим два линейных уравнения регрессии:
y 1,048 x 22,413; (21)
x 0,749 y 28,325. (22)
Средние квадратические погрешности
уравнений оцениваются по формулам:
 xy
xy yx
yx x
y
; (23)

 . (24)
. (24)Подставляя известные значения, получим:
 xy
xy yx
yx
1 ... 8 9 10 11 12 13 14 15 ... 21