Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 27.10.2023
Просмотров: 496
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Дальневосточный федеральный университет
1 ГИДРОГРАФ СТОКА И ЕГО ПОСТРОЕНИЕ
2 ХАРАКТЕРИСТИКИ СТОКА И ИХ ОПРЕДЕЛЕНИЕ
РАСЧЕТ ОРДИНАТ И ПОСТРОЕНИЕ ЭМПИРИЧЕСКОЙ И ТЕОРЕТИЧЕСКОЙ КРИВЫХ ОБЕСПЕЧЕННОСТИ РАСХОДОВ
Расчет координат теоретической кривой обеспеченности
ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ГИДРОЛОГИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ
В соответствии с СП 33-101-2003 [5] эти параметры могут быть определены одним из следующих методов:
-
методом приближенно наибольшего правдоподобия; -
методом моментов; -
графоаналитическим методом (допускается на начальных стадиях проектирования). При расчете методом приближенно наибольшего правдоподобия коэффициенты Сvи
 Сsопределяются в зависимости от статистик 2 и 3, вычисляемых по формулам:
Сsопределяются в зависимости от статистик 2 и 3, вычисляемых по формулам:
n
i1
2
lgki
(9)
n k
i1 i
3
lgki
(10)
 где ki– модульный коэффициент рассматриваемой гидрологической характеристики, определяемый по формуле:
где ki– модульный коэффициент рассматриваемой гидрологической характеристики, определяемый по формуле:
Q
ki Qi
0
, (11)
здесь Qi– погодичные расходы имеющегося ряда наблюдений.
По полученным значениям статистик 2 и 3 по номограммам (прил. А) определяют коэффициент вариации Cvи отношение коэффициента асимметрии Сsк коэффициенту вариации Cs/Cv.
С целью практического применения кривой Пирсона III типа и кривых трехпараметрического гамма-распределения были составлены унифицированные таблицы определения теоретических значений модульных коэффициентов (прил. Б). С помощью этих таблиц по основным параметрам – среднему значению, коэффициенту вариации Cvи коэффициенту асимметрии Cs– можно построить теоретическую кривую обеспеченности. После ее построения можно решить, как прямую задачу по определению величины расхода, так и обратную – по определению вероятности превышения любого наблюденного расхода.
Вместе с тем по кривой обеспеченности среднегодовых расходов можно оценить и водность года при известном расходе. СП [5] рекомендует в зависимости от продолжительности ряда наблюдений выделять три или пять групп лет разной водности.
При периоде наблюдений n от 15 до 30 лет выделяют три группы лет: многоводные годы (P< 33,3%), средние по водности годы (33,3% ≤ ???? ≤ 66,7%) и маловодные годы (P > 66,7%). При продолжительности наблюдений более 30 лет выделяют пять групп: очень многоводные годы (P< 16,7%), многоводные годы (16,7% ≤ P < 33,3%), средние по водности годы (33,3% ≤ ???? ≤ 66,7%), маловодные годы (66,7% < ???? ≤ 83,3%) и очень маловодные годы (P> 83,3%).
Пример расчета Задача 3.1
Рассчитать эмпирическую обеспеченность ряда расходов и построить кривую обеспеченности. Наблюдения проводились 30 лет – с 1957 по 1986 гг. Исходные данные приведены в табл. 5.
Таблица 5
Ежегодные максимальные расходы за период 1957–1986 гг.
| Годы | 1957 | 1958 | 1959 | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 |
| Qi | 350 | 280 | 312 | 346 | 295 | 250 | 110 | 120 | 380 | 325 |
| | ||||||||||
| Годы | 1967 | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 | 1974 | 1975 | 1976 |
| Qi | 312 | 155 | 514 | 276 | 290 | 215 | 98,6 | 104 | 480 | 203 |
| | ||||||||||
| Годы | 1977 | 1978 | 1979 | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | 1986 |
| Qi | 196 | 185 | 147 | 154 | 118 | 152 | 208 | 255 | 106 | 86,8 |
Расчет выполняют в форме, предложенной в табл. 3. В третьем столбце расходы располагают в убывающем порядке. После этого каждому расходу присваивают порядковый номер от 1 до 30 и по формуле (7) рассчитывают обеспеченность каждого расхода. Расчет
приведен в табл. 6. Для построения кривой необходимо знать модульные коэффициенты Кi
-
i
Qmax, i
Q0
, (12)
где Q0 – средний многолетний расход заданного ряда, определяемый по формуле (5):

0
???? = 7023,4 = 234 м3/с.
30
Расчет координат эмпирической кривой обеспеченности
Таблица 6
| Годы | Qmax, i, м3/с | Qmax, i, м3/с (в убывающем порядке) | m | P m100% n 1 | K Qmax,ii Q 0 |
| 1957 | 350 | 514 | 1 | 3,2 | 2,196 |
| 1958 | 280 | 480 | 2 | 6,5 | 2,050 |
| 1959 | 312 | 380 | 3 | 9,7 | 1,623 |
| 1960 | 346 | 350 | 4 | 12,9 | 1,495 |
| 1961 | 295 | 346 | 5 | 16,1 | 1,478 |
| 1962 | 250 | 325 | 6 | 19,4 | 1,388 |
| 1963 | 110 | 312 | 7 | 22,6 | 1,333 |
| 1964 | 120 | 312 | 8 | 25,8 | 1,333 |
| 1965 | 380 | 295 | 9 | 29,0 | 1,260 |
| 1966 | 325 | 290 | 10 | 32,3 | 1,239 |
| 1967 | 312 | 280 | 11 | 35,5 | 1,196 |
| 1968 | 155 | 276 | 12 | 38,7 | 1,179 |
| 1969 | 514 | 255 | 13 | 41,9 | 1,089 |
| 1970 | 276 | 250 | 14 | 45,2 | 1,068 |
| 1971 | 290 | 215 | 15 | 48,4 | 0,918 |
| 1972 | 215 | 208 | 16 | 51,6 | 0,888 |
| 1973 | 98,6 | 203 | 17 | 54,8 | 0,867 |
| 1974 | 104 | 196 | 18 | 58,1 | 0,837 |
| 1975 | 480 | 185 | 19 | 61,3 | 0,790 |
| 1976 | 203 | 155 | 20 | 64,5 | 0,662 |
| 1977 | 196 | 154 | 21 | 67,7 | 0,658 |
| 1978 | 185 | 152 | 22 | 71,0 | 0,649 |
| 1979 | 147 | 147 | 23 | 74,2 | 0,628 |
| 1980 | 154 | 120 | 24 | 77,4 | 0,513 |
| 1981 | 118 | 118 | 25 | 80,6 | 0,504 |
| 1982 | 152 | 110 | 26 | 83,9 | 0,470 |
| 1983 | 208 | 106 | 27 | 87,1 | 0,453 |
| 1984 | 255 | 104 | 28 | 90,3 | 0,444 |
| 1985 | 106 | 98,6 | 29 | 93,5 | 0,421 |
| 1986 | 86,8 | 86,8 | 30 | 96,8 | 0,371 |
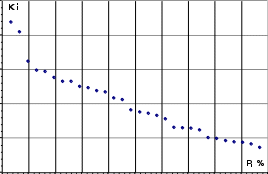
Далее строят кривую эмпирической обеспеченности по данным пятого и шестого столбцов. Обычно на графике точки эмпирической кривой не соединяют линией. На эти точки накладывают теоретическую кривую после расчета ее координат.
График эмпирической кривой приведен на рис. 3.
 2,50
2,502,00
1,50
1,00
0,50
0,00
0,0 10,0 20,0 30,0 40,0 50,0 60,0 70,0 80,0 90,0 100,0
Рис. 3. График эмпирической кривой
Задача 3.2
Построить теоретическую кривую обеспеченности и найти расход 1% вероятности превышения.
Расчет удобно выполнять в табличной форме. Для найденных по формуле (12)
модульных коэффициентов (они приведены в табл. 6) рассчитываем
lg ki, входящие в
формулу (9), и произведение
lg ki ki, входящие в формулу (10). Рассчитанные значения
записываем в столбцах3 и 4, как показано в табл. 7.
Для определения статистики 2
по формуле (9) надо просуммировать с учетом знаков
числа 3-го столбца и разделить на 29 (n = 30):
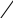 2 1,4909 30 1 0,0514 .
2 1,4909 30 1 0,0514 .Аналогично суммируют значения 4-го столбца и рассчитывают 3 :
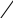 3 1,413830 1 0,0487 .
3 1,413830 1 0,0487 .На номограмме, приведенной в прил. А, по оси ординат показаны значения 2, по оси абсцисс – 3. На пересечении значений – 0,0514 и 0,0487 определяют точку О. От этой точки проводят вверх по ближайшей кривой линию до самой верхней огибающей, на которую нанесены значения коэффициента вариации Cvс точностью до 0,01. В данном примере коэффициент вариации Cv= 0,49. Чтобы определить соотношение Cs/Cv, надо провести из точки О линию (вправо, вдоль прямой) до крайней правой огибающей, на которой показаны соотношения Cs/Cvв виде Cs= n Cv.