Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx

аналогов коэффициент корреляции всегда должен быть положительным. Это вытекает из главного условия при выборе рек-аналогов – синхронности колебания стока.

Связь между величинами может быть показана графически (рис. 5).

а) б) в)

Х
Рис. 5. Графическая интерпретация связи между расходами двух рек:

а) тесная связь; б) слабая связь; в) связь отсутствует
Оценку достоверности (неслучайности) коэффициента корреляции, определенного по непродолжительному ряду наблюдений, проверяют с помощью коэффициента достоверности К_д. Он равен отношению r к его среднеквадратическому отклонению:

r n1

K_Д

1 r²

, (15)

где п– число членов ряда; r– коэффициент корреляции.

При К_д < 1 – связь отсутствует; при 1 ≤ К_д ≤ 3 существует тенденция; при К_д > 3 коэффициент корреляции считается достоверным.

Уравнениярегрессии, связывающие характеристики хи у, имеют вид:

y y

 r^^y x x

^; (16)


0 0

x

x x₀

 r^^x

 _y

 y y₀

^, (17)

где х₀ и у₀ – среднеарифметические значения членов каждого ряда; r– коэффициент корреляции; _х и

_y – среднеквадратические отклонения ряда хи ряда у.

Среднеквадратическиеотклоненияхи уопределяются по формулам:


_x
 _y

; (18)

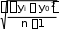, (19)

где п– число членов ряда; х_iи у_i– соответственно, наблюденные значения рассматриваемых характеристик.

Коэффициенты ???? ^^????

_????

и ???? ^^????

_????

уравнений (16) и (17) определяют угол наклона прямой

регрессии к оси ординат и оси абсцисс и называются коэффициентамирегрессии. Оба уравнения (16) и (17) имеют общую точку с координатами х₀ и у₀, т.е. пересекаются в точке, соответствующей средним значениям расхода.

Ниже приведена последовательность нахождения уравнений регрессии.

Построить график связи между значениями стока приводимого ряда наблюдений и ряда-аналога за совместный период наблюдений (графическая оценка наличия связи).
Рассчитать значение коэффициента корреляции r. Определить по его величине наличие связи между параметрами.
Сделать оценку достоверности (К_Д) коэффициента корреляции.
Определить среднеквадратические отклонения по хи у.
Рассчитать коэффициенты регрессии.
Записать уравнения регрессии.
Восстановить недостающие значения расходов в приводимом ряду. Расчет удобно вести в табличной форме (табл. 9).

Таблица 9

Расчет составляющих уравнения регрессии

x_i	y_i	∆х_i= = х_i-х₀	∆у_i= = у_i-у₀	(х_i-х₀) (у_i - у₀)	(х_i-х₀)²	(у_i-у₀)²	(∆х_i+∆у_i)²
1	2	3	4	5	6	7	8


		 = 0	 = 0				

Примечание. При расчетах делается проверка построчная и по столбцам:

2
^–_x_i 0 ^и_ y_i 0 ⁽^про^в^е^р^ка^п^о^столб^ц^а^м);

– x_i

  y_i

 x²  2  x_i

  y_i

  y² (проверка по строкам – ([3] + [4])2 = [6] + 2[5] + [7]);

i

i
^–x_i

 y_i

² x²  2  x

  y_i

  y²

– контроль сумм: берут последнюю

i

i

i
строку таблицы – [8] =  [6] + 2  [5] +  [7].

Метод корреляции широко используется в гидрологии для удлинения гидрологических рядов, определения нормы стока рек, имеющих непродолжительные ряды наблюдений.

Продолжительность периода наблюдений считают достаточной, если рассматриваемый период репрезентативен (представителен), а относительная средняя квадратическая погрешность расчетного значения исследуемой гидрологической характеристики не превышает 10% для годового и сезонного стоков и 20% – для максимального и минимального стоков.

Если относительные средние квадратические погрешности превышают указанные пределы и период наблюдений нерепрезентативен, необходимо осуществить приведение рассматриваемой гидрологической характеристики к многолетнему периоду (СП [5], раздел 6). Приведение осуществляется посредством подбора рек-аналогов и расчетом уравнений регрессии.

В соответствии с СП [5] при выборе рек-аналогов необходимо учитывать условия:

однотипность стока реки-аналога и исследуемой реки;
географическую близость расположения водосборов;
однородность условий формирования стока, сходство климатических условий, однотипность почв (грунтов) и гидрогеологических условий, близкую степень озерности, залесенности, заболоченности и распаханности водосборов;
средние высоты водосборов не должны существенно отличаться, для горных и полугорных районов следует учитывать экспозицию склона и гипсометрию;
отсутствие факторов, существенно искажающих естественный речной сток (регулирование стока, сбросы воды, изъятие стока на орошение и другие нужды).

В приведенном ниже практическом задании вопрос о выборе рек-аналогов не решается. Предлагается проверить, можно ли использовать назначенную реку в качестве реки-аналога.

Пример расчета

Проверить наличие корреляционной связи между расходами двух рек. При наличии связи составить уравнение регрессии и удлинить ряд. Исходные данные приведены в табл. 10.

Таблица 10

Среднегодовые расходы рек по данным наблюдений с 1940 по 1968 гг.

Год	^Qиссл ⁽^Xi⁾	^Qанал ⁽^Yi⁾	Год	^Qиссл ⁽^Xi⁾	^Qанал ⁽^Yi⁾
1940	–	61	1955	–	84
1941	–	206	1956	–	320
1942	–	135	1957	–	46,3
1943	–	605	1958	78,5	75,5
1944	–	46,8	1959	86,6	145
1945	–	196	1960	108	140
1946	–	356	1961	73,4	145
1947	–	109	1962	449	296
1948	–	115	1963	92,8	135
1949	–	67,5	1964	209	350
1950	644	813	1965	149	317
1951	–	300	1966	149	81
1952	–	64	1967	103	17,6
1953	–	97	1968	376	392
1954	–	47,3

Смотрите также файлы

Решение Составим таблицу решения для данной задачи (табл1) в ней будет четыре строки,так как владелец магазина может выбирать из четырех вариантов действий (закупить 1,.docx

Практических заданий по дисциплине основы организации труда.docx

Методические рекомендации по написанию, подготовке и оформлению курсовой работы по дисциплине Экономическая теория.docx

Тема рефератов.docx

Применение эффективных методов диагностики, лечения и профилактики маститов у коров.rtf

Файл: Практикум Составители Л. И. Шевелева, В. И. Максименко, А. Г. Голикова.docx

Пример расчета

Смотрите также файлы

Информация

Списки файлов

Дополнительно