Файл: Лабораторная работа за 4 семестр По дисциплине "Теория информации, данные, знания".docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 429
Скачиваний: 26
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
ФАКУЛЬТЕТ ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ
Лабораторная работа за _4_ семестр
По дисциплине “Теория информации, данные, знания”
Вариант 4
Фамилия: Сетова
Имя: Кристина
Отчество: Павловна
Курс: 2
Студ. Билет №: 2010534
Группа №: ИБ-06c
Дата сдачи работы:
Санкт-Петербург
2022
Формулировка задания
Задача 1
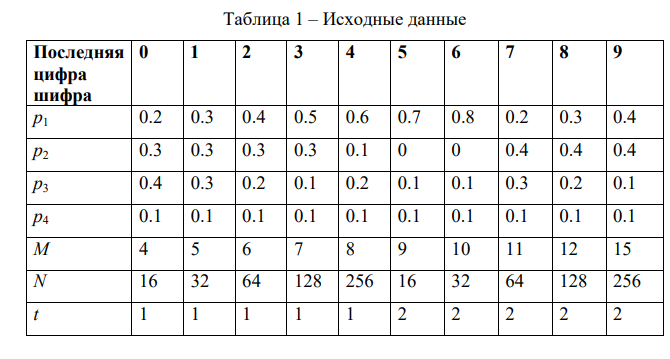
Источник сообщений выдает символы из алфавита A = {ai}, i = 1,…,4 с
вероятностями (см. таблицу 1) p1, p2, p3, p4. Найти энтропию и избыточность
источника сообщений.
Задача 2
Рассмотрим следующий процесс: мы замеряем некоторую величину ξ,
которая является количеством фотонов, которые регистрируются
фоточувствительной пластиной. Пусть источник света в единицу времени
генерирует N фотонов. Каждый фотон с вероятностью p1 может рассеяться на
частицах среды, находящейся между источником и пластиной и не достичь
фоточувствительной пластины. С вероятностью p2 фотон, достигший
фоточувствительной пластины, может быть зарегистрирован пластиной.
Какое количество информации содержится в сообщении, что
зарегистрировано M фотонов?
Задача 3
Первичный алфавит состоит из трех знаков с вероятностями p1, p2, p.
При этом p1 и p2 заданы в табл.1 и p1+p2+p=1. Для передачи по каналу без
помех используется равномерный двоичный код. Средняя длительность
передачи одного элемента сообщения в канале τ=10-6с. Определить
пропускную способность канала и скорость передачи информации. Можно
ли приблизить скорость передачи к пропускной способности данной
системы?
Задача 4
Сколько информационных и проверочных символов содержится в
двоичном коде, исправляющем ровно t ошибок при общем числе
разрешенных кодовых комбинаций, равном N (см. таблицу 1).
Задача 1
Задание: Источник сообщений выдает символы из алфавита
с вероятностями:
Найти энтропию и избыточность источника сообщений.
Решение: Энтропия находится по следующей формуле:
Подставим значения в формулу и получим значение энтропии:
H(a) = -(0.6*log(0.7, 2) + 0.1*log(0.1,2) + 0.2*log(0.2,2) + 0.1*log(0.1,2)) = 1.4375151416528
Теперь найти источник избыточности сообщений, она находится по формуле:
где 
, а M в свою очередь – это количество различных символов в алфавите, в нашем случае их 4. Посчитаем избыточность источника:
R= 1-( 1.4375151416528/2 = 0.7187575708264
Ответ: энтропия источника равна 1.4375151416528, а избыточность равна 0.7187575708264.
Задача 2
Задание: рассмотрим следующий процесс: мы замеряем некоторую величину ξ, которая является количеством фотонов, которые регистрируются фоточувствительной пластиной. Пусть источник света в единицу времени генерирует 256 фотонов. Каждый фотон с вероятностью
может рассеяться на частицах среды, находящейся между источником и пластиной и не достичь фоточувствительной пластины. С вероятностью 
фотон, достигший фоточувствительной пластины, может быть зарегистрирован пластиной. Какое количество информации содержится в сообщении, что зарегистрировано 
фотонов?
Решение: Чтобы найти количество информации в сообщении, используем формулу Хартли:
где p – вероятность интересующего нас события. Для нахождения этой вероятности поделим интересующее нас количество исходов (8) на количество всех возможных (256). Подставим значения в формулу и получим ответ:I = log(1/(8/256), 2)
Ответ: В сообщении, что зарегистрировано 8 фотонов из 256, содержится примерно 32 бит информации.
Задача 3
Задание: Первичный алфавит состоит из трех знаков с вероятностями p1 =0.6 p2 = 0.1 p. При этом
. Для передачи по каналу без помех используется равномерный двоичный код. Средняя длительность передачи одного элемента сообщения в канале 
с. Определить пропускную способность канала и скорость передачи информации. Можно ли приблизить скорость передачи к пропускной способности данной системы?Решение: Пропускная способность канала находится по следующей формуле:
где m – вторичный алфавит (для двоичных сигналов 
), 
– длительность элементарного импульса в канале, которая находится по формуле:
а T в свою очередь равняется 
. Таким образом получаем финальную формулу:
Теперь найдём скорость передачи информации по формуле:
где H – это энтропия. Так как τ уже известно, остается найти энтропию. Сделаем это:
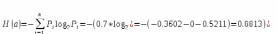
Наконец получим скорость передачи информации:
Ответ: пропускная способность канала равна 2*10-6 бит/с, а скорость передачи информации равна
.Задача 4
Задание: Сколько информационных и проверочных символов содержится в двоичном коде, исправляющем ровно
ошибок при общем числе разрешенных кодовых комбинаций, равном 
?Решение: так как число разрешенных кодовых комбинаций равняется 2k, где k число информационных символов, то получим
. Далее найдем число проверочных символов. Количество проверочных символов находится по формуле:
так как количество символов должно быть целым числом, необходимо r, полученное с помощью данного уравнения, округлить до ближайшего большего целого числа. При r=2 получим, что правая часть окажется меньше, чем левая, при r=3 получаем 2<3. Значит, число проверочных символов равно 2.Ответ: В коде содержится 4 информационных символа и 2 проверочных.
Вывод
В данной лабораторной работе мною были выполнены задания по вычислению количества информации. Данные задачи важны для понимания искомой информации и вычисления ее из других значений. В дальнейшем данные навыки могут быть применены в более глобальных работах для ускорения процессов обработки данных и улучшению взаимодействия программных элементов с данными баз данных.