Образовательное учреждение высшего образования

« Южно-Уральский институт управления и экономики»


КОНТРОЛЬНАЯ РАБОТА


По дисциплине «Эконометрика»
Вариант № 8

Выполнил(а) студент(ка)

___________________________________________________________

(Фамилия, имя, отчество)

___________________________________________________________

(Адрес проживания)
Группа ______________________
Дата отправления «__» ____201_ г.

Результат проверки____________________

Проверил преподаватель _______________

Дата проверки________________________

г. Челябинск, 2023

Содержание

Задача 1……………………………………………………………………………..	3
Задача 2……………………………………………………………………………..	12

Задача 1

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (У, млн. руб) от объема капиталовложений (Х, млн. руб).

Требуется:

1. 
   Для характеристики У от Х построить следующие модели:
   

• 
  линейную,
  
• 
  степенную,
  
• 
  показательную,
  
• 
  гиперболическую.
  

Оценить каждую модель, определив:

• 
  индекс корреляции,
  
• 
  среднюю относительную ошибку,
  
• 
  коэффициент детерминации,
  
• 
  F – критерий Фишера.
  

Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

Рассчитать прогнозное значение результативного признака, если прогнозное значение фактора увеличится на 110% относительно среднего уровня.

Результаты расчетов отобразить на графике.

Вариант 8

Таблица 1

Y	64	56	52	48	50	46	38
X	64	68	82	76	84	96	100

---

Решение:

Построение линейной модели парной регрессии.

Определим линейный коэффициент парной корреляции по следующей формуле, используя данные таблицы 2:



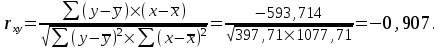
Таблица 2

t	y	x	yx	x 2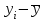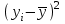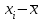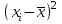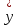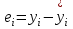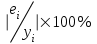
1	64	64	4096	4096	13,43	180,36	-17,4	303,8	60,2	3,84	6,000
2	56	68	3808	4642	5,43	29,485	-13,4	180,36	58,0	-1,96	3,500
3	52	82	4264	6724	1,43	2,0449	0,57	0,3249	50,3	1,74	3,346
4	48	76	3648	5776	-2,57	6,6049	-5,43	29,485	53,6	-5,56	11,583
5	50	84	4200	7056	-0,57	0,3249	2,57	6,6049	49,2	0,84	1,680
6	46	96	4416	9216	-4,57	20,885	14,57	212,28	42,6	3,44	7,478
7	38	100	3800	10000	-12,6	158,0	18,57	344,84	40,4	-2,36	6,211
Итого	354,0	570,0	28232	47492	0,01	397,71		1077,7		-0,02	39,798
Ср. знач	50,57	81,43	4033,14	6784,57							5,685

---

Можно сказать, что связь между объемом капиталовложений X и объемом выпуска продукции Y обратная, достаточно сильная.

Уравнение линейной регрессии имеет вид: .

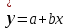Значения параметров a и b линейной модели определим, используя данные таблицы 2.



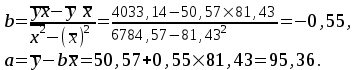
Уравнение регрессии имеет вид: .

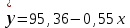С увеличением объема капиталовложений на 1 млн руб. объем выпускаемой продукции уменьшится в среднем на 550 тыс. руб. Это свидетельствует о неэффективности работы предприятий, и необходимо принять меры для выяснения причин и устранения этого недостатка.

Рассчитаем коэффициент детерминации:

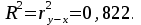
Вариация результата Y (объема выпуска продукции) на 82,2% объясняется вариацией фактора X (объемом капиталовложений).

Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:

;

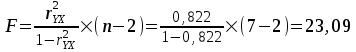FF_табл = 6,61 для =0,05; k₁ = m = 1, k₂ = n – m – 1 = 5/

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F F_табл.

Определим среднюю ошибку:

.

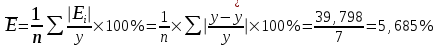В среднем расчетные значения для линейной модели отличаются от фактических значений на 5,685%.

Построение степенной модели парной регрессии

Уравнение степенной модели имеет вид: .

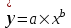Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

lg =

---

lg a +b lg x. данные приведены в таблице 3

Таблица 3

	Факт. Y(t)	lg(y)	Переменная X(t)	lg(x)
1 2 3 4 5 6 7  28	64,0 56,0 52,0 48,0 50,0 46,0 38,0 354,0	1,806 1,748 1,716 1,681 1,699 1,633 1,580 11,893	64 68 82 76 84 96 100 570	1,806 1,833 1,914 1,881 1,924 1,982 2,000 13,340
Сред. знач	50,5714	1,699	81,429	1,906

Обозначим Y = lg , X = lg x, A = lg a. тогда уравнение примет вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.

	y	Y	x	X	YX	X2		Ei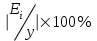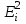
1 2 3 4 5 6 7	64 56 52 48 50 46 38	1,8062 1,7482 1,7160 1,6812 1,6990 1,6628 1,5798	64 68 82 76 84 96 100	1,8062 1,8325 1,9138 1,8808 1,9243 1,9823 2,000	3,2623 3,2036 3,2841 3,1621 3,2693 3,2960 3,1596	3,2623 3,3581 3,6627 3,5375 3,7029 3,9294 4,0000	61,294 58,066 49,133 52,580 48,088 42,686 41,159	2,706 -2,066 2,867 -4,580 1,912 3,314 -3,159	4,23 3,69 5,51 9,54 3,82 7,20 8,.31	7,322 4,270 8,220 20,976 3,657 10,982 9,980
итого	354	11,8931		13,3399	22,6370	25,4528		0,51	42,32	65,407

---

Таблица 3

---

Смотрите также файлы

• На свете есть особый шар.docx

• Интересный способ посадки огурцов.doc

• Самостоятельная работа по теме Цель занятия формирование знаний содержания учебного предмета математика.docx

• Лекции по теоретической метрологии.doc

• Литература вов, "деревенская проза", "городская проза", историческая романтика, "лагерная проза".docx