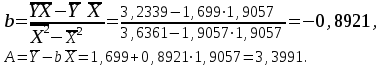
Уравнение регрессии будет иметь вид: Y = 3,3991 – 0,8921X.

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.



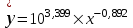
Получим уравнение степенной модели регрессии: = 2506,915  x^-0,892.

Определим индекс корреляции:



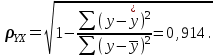
связь между показателем y и фактором x можно считать достаточно сильной.

Коэффициент детерминации равен 0,836:



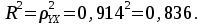
Вариация результата Y (объем выпуска продукции) на 83,6% объясняется вариацией фактора X (объемом капиталовложений).

Рассчитаем F-критерий Фишера:



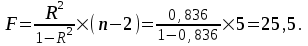
F F_табл = 6,61 для  = 0,05; k₁ = m = 1, k₂ = n –m –1 = 5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F F_табл.

Средняя относительная ошибка



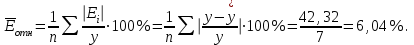
В среднем расчетные значения 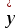для степенной модели отличаются от фактических значений на 6,04%.
Построение показательной функции

Уравнение показательной кривой: .

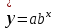Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:

.

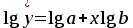Обозначим:

---

.

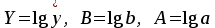
Получим линейное уравнение регрессии:

Y=A+Bx.

Рассчитаем его параметры, используя данные таблицы 4.


Таблица 4

t	y	Y	x	Yx	x2		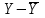		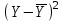		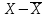	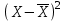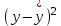Ei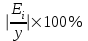
1 2 3 4 5 6 7	64 56 52 48 50 46 38	1,8062 1,7482 1,7160 1,6812 1,.6990 1,6628 1,5798	64 68 82 76 84 96 100	115,60 118,88 140,71 127,77 142,71 159,62 157,98	4096 4624 6724 5776 7056 9216 10000	0,1072 0,0492 0,0170 -0,017 0,0000 -0,036 -0,119	0,0115 0,0024 0,0003 0,0003 0,0000 0,0013 0,0142	-17,43 -13,43 0,57 -5,43 2,57 14,57 18,57	303,76 180,33 0,33 29,47 6,61 212,33 344,90	60,6 58 49,7 53,1 48,6 42,5 40,7	11,464 3,9632 5,4221 25,804 2,0031 11,933 7,3132	3,3859 -1,991 2,3285 -5,08 1,4153 3,4544 -2,704
итого	354	11,8931	550	963,28	47495		0,0300		1077,7		67,903	0,8093
сред знач	50,57	1,6990	81,4	137,61	6785

---

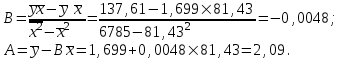
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:



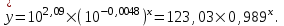
Определим индекс корреляции:

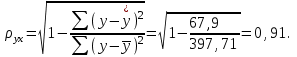
Связь между показателем y и фактором x можно считать достаточно сильной.

Индекс детерминации: R² = 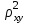= 0,91² = 0,828.

Вариация результата Y (объема выпуска продукции) на 82,8% объясняется вариацией фактора X (объемом капиталовложений).

Рассчитаем F-критерий Фишера:

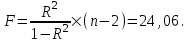
F F_табл = 6,61 для  = 0,05; k₁=m=1, k₂ = n – m – 1 = 5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F F_табл.

Средняя относительная ошибка:

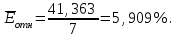
В среднем расчетные значения для показательной функции отличаются от фактических на 5,909%.

Построение гиперболической функции

Уравнение гиперболической функции:

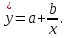
Произведем линеаризацию модели путем замены X= 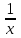. В результате получим линейное уравнение .

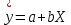Рассчитаем его параметры по данным таблицы 5.



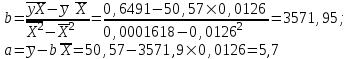
Получим следующее уравнение гиперболической модели: .

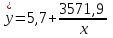Определим индекс детерминации: R² = 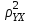= 0,914² = 0,835.

Таблица 5.

t	y	x	X	yX	X2					Ei
1 2 3 4 5 6 7	64 56 52 48 50 46 38	64 68 82 76 84 96 100	0,0156 0,0147 0,0122 0,0132 0,0119 0,0104 0,0100	1,0000 0,8235 0,6341 0,6316 0,5952 0,4792 0,3800	0,0002441 0,0002163 0,0001487 0,0001731 0,0001417 0,0001085 0,0001000	13,43 5,43 1,43 -2,57 -0,57 -4,57 -12,57	180,33 29,47 2,04 6,61 0,32563 20,90 158,04	61,5 58,2 49,3 52,7 48,2 42,9 41,4	6,1954 4,9637 7,5089 22,078 3,1591 9,5648 11,69	2,489 -2,228 2,740 -4,699 1,777 3,093 -3,419	3,889 3,978 5,270 9,789 3,555 6,723 8,997
итого	354		0,0880	4,5437	0,0011325		397,71	354,2	65,159	-0,246	42,202
сред знач	50,57		0,0126	0,6491	0,0001618						6,029

---

Вариация результата Y (объема выпуска продукции) на 83,6% объясняется вариацией фактора X (объемом капиталовложений).

F-критерий Фишера:



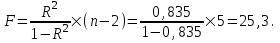
F F_табл= 6,61 для  = 0,05; k₁=m=1, k₂ = n – m – 1 = 5.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F F_табл.

Средняя относительная ошибка:

---

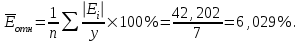
В среднем расчетные значения для гиперболической модели отличаются от фактических значений на 6,029%.

Выбор лучшей модели

Для выбора лучшей модели построим сводную таблицу 6 результатов.

Таблица 6.

Параметры Модель	Коэффициент детерминации R2	F-критерий Фишера	Индекс корреляции YX (ryx)	Средняя относительная ошибка Eотн
Линейная	0,822	23,09	0,907	5,685
Степенная	0,828	24,06	0,910	6,054
Показательная	0,828	24,06	0,910	5,909
Гиперболичская	0,835	25,30	0,914	6,029

Все модели имеют примерно одинаковые характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации R² имеет гиперболическая модель. Ее можно взять в качестве лучшей для построения прогноза.
Расчет прогнозного значения результативного показателя

Прогнозное значение результативного признака (объема выпуска продукции) определяется по уравнению гиперболической модели, подставив в него планируемую (заданную по условию) величину объема капиталовложений:

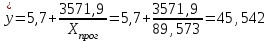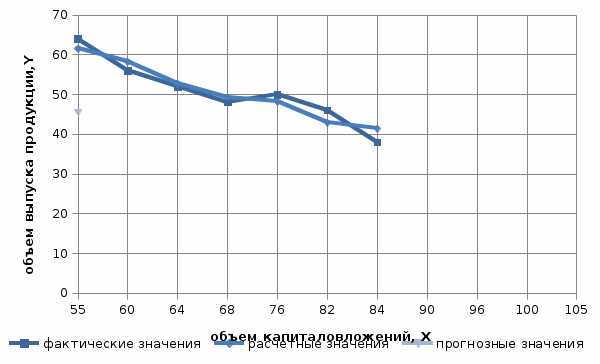
(млн руб.).

Фактические, расчетные и прогнозные значения по лучшей модели отображаются на графике.

---

Смотрите также файлы

• На свете есть особый шар.docx

• Интересный способ посадки огурцов.doc

• Самостоятельная работа по теме Цель занятия формирование знаний содержания учебного предмета математика.docx

• Лекции по теоретической метрологии.doc

• Литература вов, "деревенская проза", "городская проза", историческая романтика, "лагерная проза".docx