Рисунок 1  Прогноз по лучшей модели


Задача 2

По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам (X₁), ставки по депозитам (X₂) и размера внутрибанковских расходов (X₃).

Требуется:

1. 
   Построить множественную модель и оценить ее.
   
2. 
   Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.
   
3. 
   Рассчитать параметры модели.
   
4. 
   Для характеристики модели определить:
   

• 
  линейный коэффициент множественной корреляции,
  
• 
  коэффициент детерминации,
  
• 
  средние коэффициенты эластичности, бетта –, дельта – коэффициенты.
  

Дать их интерпретацию.

5. 
   Осуществить оценку надежности уравнения регрессии.
   
6. 
   Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
   
7. 
   Построить точечный и интервальный прогнозы результирующего показателя.
   
8. 
   Отразить результаты расчетов на графике.
   

Выполнение задач отразить в аналитической записке, приложить компьютерные распечатки расчетов.

Вариант 8

Таблица 7

Y	X1	X2	X3
150	86	60	56
154	94	68	48
146	100	64	52
134	96	72	58
132	134	78	66
126	114	88	62
134	122	90	48
126	118	82	66
88	130	92	70
120	108	94	68

---

Решение:

Выбор факторных признаков для построения модели осуществляется с помощью матрицы коэффициентов парной корреляции. Для её построения необходимо:

• 
  выбрать Сервис->Анализ данных->Корреляция
  
• 
  заполнить необходимые поля диалогового меню (рисунок 2)
  

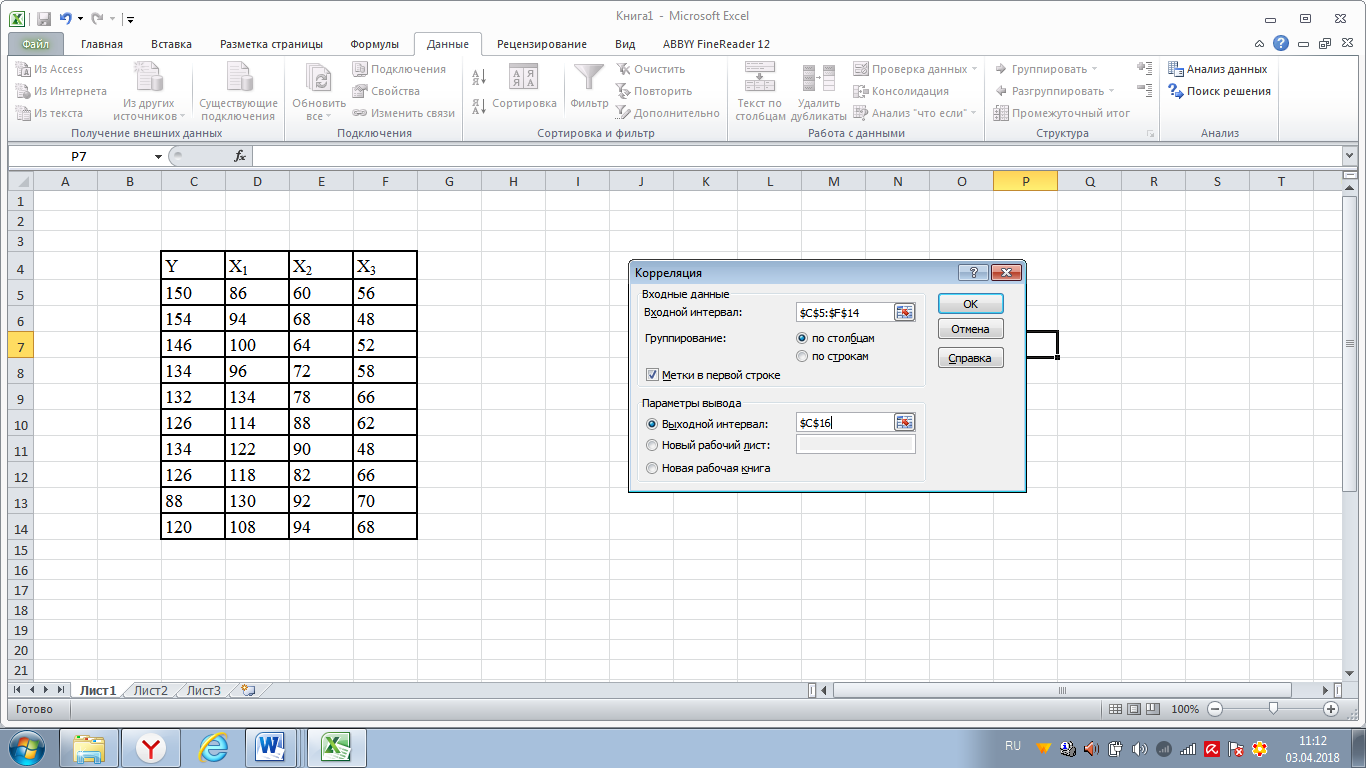
Рисунок 2  Ввод параметров инструмента «Корреляция»
Таблица 8  Коэффициенты парных корреляций

	Y	X1	X2	X3
Y	1
X1	-0,68368	1
X2	-0,77787	0,717489	1
X3	-0,76954	0,535	0,537046	1

---

Для выявления явления мультиколлинеарности необходимо проанализировать коэффициенты парной корреляции между факторными признаками. Если имеют место коэффициенты, значение которых по модулю больше 0,8, то, следовательно, мультиколлинеарность присутствует, и это явление необходимо устранять. Если же значения коэффициентов парной корреляции между факторными признаками, взятые по модулю, меньше величины 0,8, то явление мультиколлинеарности отсутствует, и, следовательно, все факторные признаки можно включать в модель множественной регрессии. Таким образом, в нашем случае все факторы можно включать в модель множественной регрессии (рисунок 3).

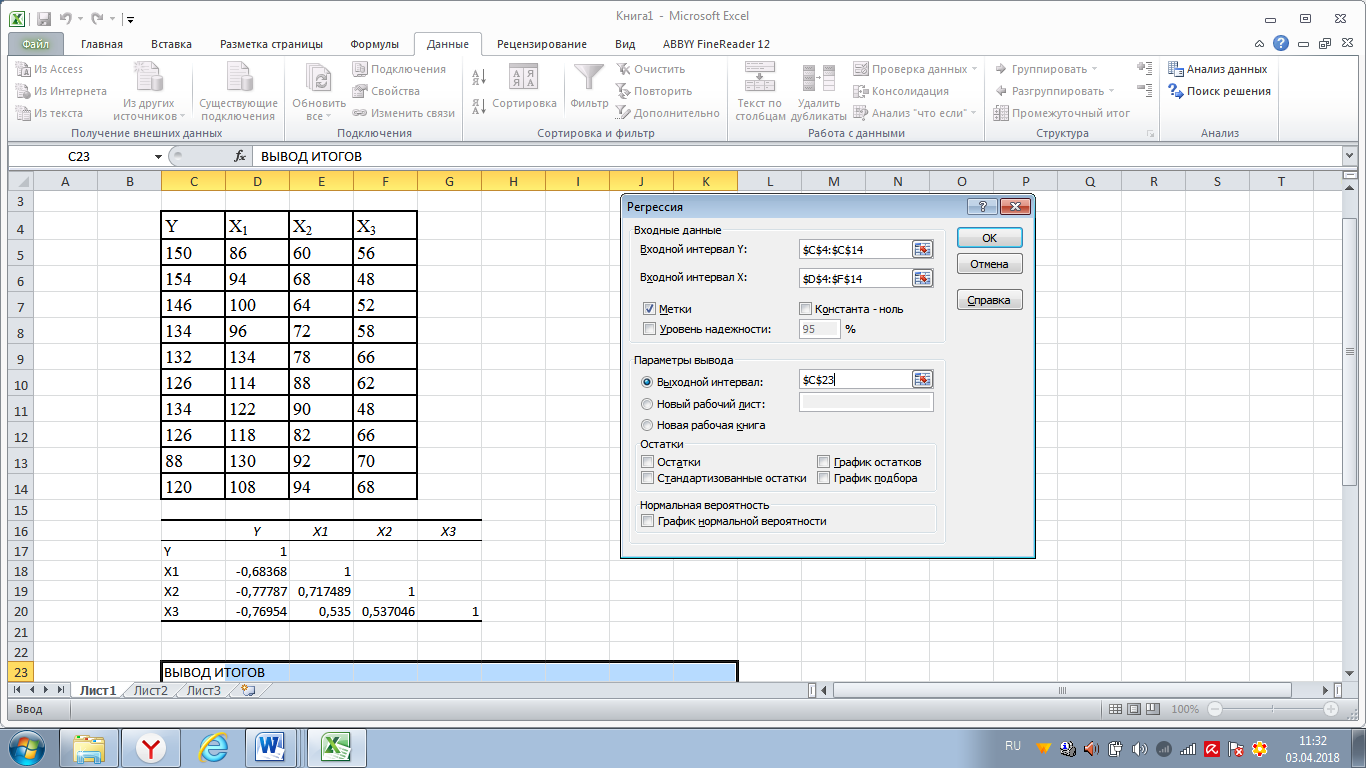
Рисунок 3  Ввод параметров регрессии
Результаты построение множественной регрессии представлены в таблице 9.

Таблица 9  Результаты построение множественной регрессии

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R		0,885925
R-квадрат		0,784863
Нормированный R-квадрат		0,677294
Стандартная ошибка		10,6344
Наблюдения		10
Дисперсионный анализ
	df				SS			MS			F			Значимость F
Регрессия	3				2475,457			825,1523			7,29639			0,019941
Остаток	6				678,543			113,0905
Итого	9				3154
	Коэффициенты		Стандартная ошибка			t-статистика			P-Значение			Нижние 95%			Верхние 95%			Нижние 95,0%			Верхние 95,0%
Y-пересечение	262,4049		28,95598			9,062201			0,000101			191,5522			333,2576			191,5522			333,2576
X1	-0,13218		0,326956			-0,40429			0,700017			-0,93222			0,667847			-0,93222			0,667847
X2	-0,67525		0,428508			-1,57581			0,166139			-1,72377			0,373273			-1,72377			0,373273
X3	-1,07119		0,528535			-2,02671			0,089069			-2,36447			0,222092			-2,36447			0,222092

---

На основании полученных данных можно записать уравнение множественной регрессии

Y=262,4-0,1222*X1-0,6753Х2-1,0712*X3
Оценим качество построенной модели множественной регрессии по следующим направлениям:

• 
  Коэффициент детерминации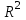 = 0,7849 достаточно близок к 1, следовательно, качество модели можно признать высоким.
  
• 
  Критерий Фишера F = 7,2964 > Fтабл = 4,74 , следовательно, уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования экономических процессов.
  

Для вычисления Fтабл необходимо определить:

- степень свободы числителя m=2 (число факторных признаков);

- степень свободы знаменателя n-m-1=10-2-1=7;

- уровень значимости 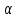=0,05.

Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности,  - и  - коэффициентов.

Коэффициент эластичности определяется:

,

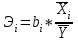где 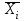- среднее значение соответствующего факторного признака,

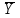- среднее значение результативного признака.

b_i – коэффициенты регрессии соответствующих факторных признаков.

ß-коэффициент определяется по следующей формуле:

---

,

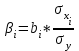где 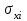- среднеквадратическое отклонение (СКО) соответствующего факторного признака (рассчитывается как корень квадратный из дисперсии признака),

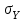- СКО результативного признака.

∆-коэффициент определяется по следующей формуле:

,

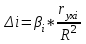где 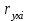- коэффициент парной корреляции результативного и соответствующего факторного признаков,

- коэффициент детерминации.

На рисунке 4 представлены формулы расчетов описанных выше коэффициентов
Таблица 10

	Y	X1	X2	X3
	150	86	60	56
	154	94	68	48
	146	100	64	52
	134	96	72	58
	132	134	78	66
	126	114	88	62
	134	122	90	48
	126	118	82	66
	88	130	92	70
	120	108	94	68
ср. зн.	131	110,2	78,8	59,4
эласт		-0,1112	-0,40618	-0,48571
дисп	350,4444	259,0667	151,2889	67,6
ско	18,72016	16,09555	12,29995	8,221922
bi		-0,13218	-0,67525	-1,07119
Bi		-0,11365	-0,44367	-0,47047
ryxi		-0,68368	-0,77787	-0,76954
deltai		0,099	0,439717	0,461283
R	0,784863

---

Смотрите также файлы

• На свете есть особый шар.docx

• Интересный способ посадки огурцов.doc

• Самостоятельная работа по теме Цель занятия формирование знаний содержания учебного предмета математика.docx

• Лекции по теоретической метрологии.doc

• Литература вов, "деревенская проза", "городская проза", историческая романтика, "лагерная проза".docx