Файл: Отчет по лабораторной работе 100 Измерение электронным секундомером интервалов времени, задаваемых по механическому секундомеру.docx
Добавлен: 29.10.2023
Просмотров: 472
Скачиваний: 38
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство железнодорожного транспорта
Федеральное государственное бюджетное
образовательное учреждение высшего образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВО ПГУПС)
Кафедра «Физика»
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 100
«Измерение электронным секундомером интервалов времени,
задаваемых по механическому секундомеру»
Выполнил студент: курса
группа:
зачетная книжка:
Преподаватель:
г. Санкт – Петербург
2021 г.
Цель работы – освоение алгоритма обработки результатов прямых многократных измерений, построение гистограммы экспериментальных значений определяемой величины и оценка параметров распределения Гаусса по кривой закона распределения.
Теоретическая часть:
В зависимости от способа получения числового значения измеряемой величины измерения делятся на прямые, косвенные, невоспроизводимые косвенные.
Прямыми называются измерения, при которых искомое значение величины получают из опытных данных. При прямых измерениях экспериментальные операции производятся над самой измеряемой величиной. Числовое значение измеряемой величины получают в экспериментальном сравнении с мерой или по показаниям приборов. Например, измерение тока амперметром, напряжения вольтметром, температуры термометром, массы на весах.
Косвенными называют такие измерения, при которых числовое значение измеряемой величины определяется по известной функциональной зависимости через другие величины, которые можно прямо измерить. При косвенных измерениях числовое значение измеряемой величины получают с участием оператора на основе прямых измерений – решением одного уравнения. К косвенным измерениям прибегают в тех случаях, когда неудобно или невозможно осуществить автоматическое вычисление известной зависимости между одной или несколькими входными величинами и измеряемой величиной. Например, мощность в цепях постоянного тока определяет оператор, умножая напряжение на ток, измеренные прямым измерением с помощью амперметра и вольтметра.
Невоспроизводимые косвенные измерения – это когда при выполнении косвенных измерений невозможно повторить наблюдения в тождественных условиях относительно одного или нескольких аргументов измеряемой функции.
При выполнении каких-либо расчетов, всегда существует погрешность этих измерений.
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Выяснить с абсолютной точностью истинное значение измеряемой величины, как правило, невозможно, поэтому невозможно и указать величину отклонения измеренного значения от истинного. Это отклонение принято называть ошибкой измерения.
В погрешность определяемой величины входят две составляющие: случайная (статистическая) и систематическая (приборная). Грубый прибор характеризуется погрешностью значительно больше случайной, поэтому при многократных измерениях результат получается практически один и тот же. Точный прибор характеризуется меньшей систематической (приборной) погрешностью по сравнению со случайной, поэтому на распределении полученных результатов измерений сказывается случайный разброс.
Исходные данные:
Таблица 1 – Характеристика приборов
| № прибора | Название | Диапазон секундомера | Цена деления | Погрешность прибора |
| 1 | Механический секундомер | 0-1800 с. | 0,2 с. | 0,1 с. |
| 2 | Электронный секундомер | 0-999,999 с. | 0,001 с. | 0,001 с. |
Таблица 2 – Таблица измерений
| № измерения (предварительный) | Алфавит | № измерения (окончательный) | ti | Δti | Δti2 |
| 1 | А | | 4,791 | | |
| 2 | Б | 1 | 4,913 | 0.064 | 0,00410 |
| 3 | В | | 5,246 | | |
| 4 | Г | 2 | 4,992 | -0,015 | 0,00022 |
| 5 | Д | | 4,814 | | |
| 6 | Е | 3 | 4,869 | 0.108 | 0,01167 |
| 7 | Ё | 4 | 4,747 | 0,230 | 0,05292 |
| 8 | Ж | 5 | 5,258 | -0,281 | 0,07894 |
| 9 | З | 6 | 5,034 | -0,057 | 0,00324 |
| 10 | И | | 5,128 | | |
| 11 | Й | 7 | 5,045 | -0,068 | 0,00462 |
| 12 | К | | 5,001 | | |
| 13 | Л | | 4,928 | | |
| 14 | М | 8 | 4,915 | 0,062 | 0,00385 |
| 15 | Н | 9 | 5,003 | -0,026 | 0,00067 |
| 16 | О | | 4,812 | | |
| 17 | П | | 4,686 | | |
| 18 | Р | | 5,241 | | |
| 19 | С | | 5,144 | | |
| 20 | Т | 10 | 4,166 | 0,811 | 0,65779 |
| 21 | У | 11 | 4,938 | 0,039 | 0,00152 |
| 22 | Ф | 12 | 4,850 | 0,127 | 0,01614 |
| 23 | Х | 13 | 5,015 | -0,038 | 0,00144 |
| 24 | Ц | 14 | 5,228 | -0,251 | 0,06298 |
| 25 | Ч | 15 | 5,161 | -0,184 | 0,03384 |
| 26 | Ш | 16 | 5,156 | -0,179 | 0,03202 |
| 27 | Щ | 17 | 5,009 | -0,032 | 0,00102 |
| 28 | Ъ | 18 | 5,078 | -0,101 | 0,01019 |
| 29 | Ы | 19 | 4,978 | -0,001 | 0,00000 |
| 30 | Ь | 20 | 4,865 | 0,112 | 0,01255 |
| 31 | Э | 21 | 4,772 | 0,205 | 0,04204 |
| 32 | Ю | 22 | 4,911 | 0,066 | 0,00436 |
| 33 | Я | | 4,960 | | |
| 34 | А | | 5,231 | | |
| 35 | Б | 23 | 5,181 | -0,204 | 0,04160 |
| 36 | В | | 4,894 | | |
| 37 | Г | 24 | 5,123 | -0,146 | 0,02130 |
| 38 | Д | | 4,891 | | |
| 39 | Е | 25 | 4,633 | 0,344 | 0,11837 |
| 40 | Ё | 26 | 4,930 | 0,047 | 0,00221 |
| 41 | Ж | 27 | 5,159 | -0,182 | 0,03311 |
| 42 | З | 28 | 5,092 | -0,115 | 0,01321 |
| 43 | И | | 5,086 | | |
| 44 | Й | 29 | 4,959 | 0,018 | 0,00033 |
| 45 | К | | 5,382 | | |
| 46 | Л | | 4,909 | | |
| 47 | М | 30 | 5,003 | -0,026 | 0,00067 |
| 48 | Н | 31 | 4,901 | 0,076 | 0,00578 |
| 49 | О | | 5,048 | | |
| 50 | П | | 5,259 | | |
| 51 | Р | | 4,765 | | |
| 52 | С | | 5,244 | | |
| 53 | Т | 32 | 4,851 | 0,126 | 0,01589 |
| 54 | У | 33 | 5,048 | -0,071 | 0,00503 |
| 55 | Ф | 34 | 5,186 | -0,209 | 0,04366 |
| 56 | Х | 35 | 4,981 | -0,004 | 0,00002 |
| 57 | Ц | 36 | 4,982 | -0,005 | 0,00002 |
| 58 | Ч | 37 | 5,027 | -0,050 | 0,00250 |
| 59 | Ш | 38 | 4,954 | 0,023 | 0,00053 |
| 60 | Щ | 39 | 5,060 | -0,083 | 0,00688 |
| 61 | Ъ | 40 | 5,137 | -0,160 | 0,02559 |
| 62 | Ы | 41 | 5,147 | -0,170 | 0,02888 |
| 63 | Ь | 42 | 4,909 | 0,068 | 0,00463 |
| 64 | Э | 43 | 4,703 | 0,274 | 0,07510 |
| 65 | Ю | 44 | 4,962 | 0,015 | 0,00023 |
| 66 | Я | | 4,936 | | |
| 67 | А | | 4,670 | | |
| 68 | Б | 45 | 5,133 | -0,156 | 0,02432 |
| 69 | В | | 4,992 | | |
| 70 | Г | 46 | 4,846 | 0,131 | 0,01717 |
| 71 | Д | | 4,917 | | |
| 72 | Е | 47 | 5,009 | -0,032 | 0,00102 |
| 73 | Ё | 48 | 5,108 | -0,131 | 0,01715 |
| 74 | Ж | 49 | 4,848 | 0,129 | 0,01665 |
| 75 | З | 50 | 4,821 | 0,156 | 0,02435 |
| 76 | И | | 5,175 | | |
| 77 | Й | 51 | 4,903 | 0,074 | 0,00548 |
| 78 | К | | 5,066 | | |
| 79 | Л | | 4,971 | | |
| 80 | М | 52 | 5,148 | -0,089 | 0,00791 |
| 81 | Н | 53 | 5,010 | 0,006 | 0,00004 |
| 82 | О | | 5,065 | | |
| 83 | П | | 4,953 | | |
| 84 | Р | | 5,093 | | |
| 85 | С | | 4,805 | | |
| 86 | Т | 54 | 4,814 | -0,171 | 0,02923 |
| 87 | У | 55 | 5,066 | -0,033 | 0,00109 |
| 88 | Ф | 56 | 5,021 | -0,044 | 0,00193 |
| 89 | Х | 57 | 4,943 | 0,034 | 0,00116 |
| 90 | Ц | 58 | 5,012 | -0,035 | 0,00122 |
| 91 | Ч | 59 | 5,043 | -0,066 | 0,00435 |
| 92 | Ш | 60 | 5,229 | -0,252 | 0,06348 |
| 93 | Щ | 61 | 4,810 | 0,167 | 0,02790 |
| 94 | Ъ | 62 | 5,031 | -0,054 | 0,00291 |
| 95 | Ы | 63 | 4,988 | -0,011 | 0,00012 |
| 96 | Ь | 64 | 4,774 | 0,203 | 0,04123 |
| 97 | Э | 65 | 5,129 | -0,152 | 0,02309 |
| 98 | Ю | 66 | 4,811 | 0,166 | 0,02757 |
| 99 | Я | | 4,999 | | |
| 100 | А | | 5,126 | | |
Расчётные формулы:
-
выборочное среднее значение: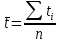
,
где ti – результат наблюдения; n – количество измерений.
-
отклонения отдельных результатов наблюдений от среднего:
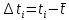,где i- номер измерения; ti – результат наблюдения;
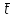– среднее значение результатов.-
расчет среднеквадратичной погрешности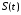
отдельного результата наблюдения: 
,
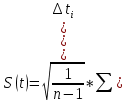где n – количество измерений;
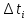-отклонение от среднего результата.-
среднеквадратичную погрешность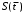
среднего арифметического результата измерений по формуле: 
,
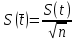где
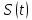- среднеквадратичной погрешности отдельного результата; n – количество измерений -
случайная погрешность: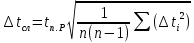
,
где
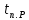- коэффициент Стьюдента; n – количество измерений; 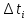-отклонение от среднего результата.-
ширина интервала: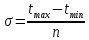
где tmax – максимальное значение времени; tmin – минимальное значение времени; n – число ячеек массива.
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
-
Для начала исследуем дрейф: для этого построим график зависимости результатов наблюдений от порядкового номера наблюдения:
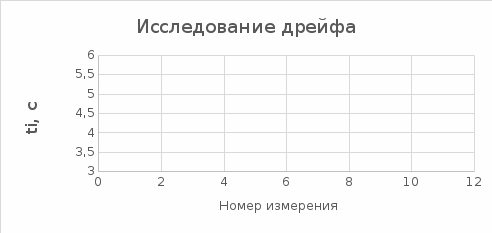
По графику определяем, что дрейф отсутствует.
-
Статистический анализ выборки
Выборочное среднее значение:
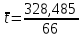= 4,977 с Отклонение отдельных результатов наблюдений от среднего:
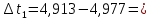0,064 с
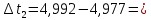-0,015 с 
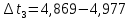= 0,108 с…
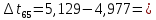- 0,152 с 
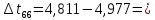0,166 с Результаты записываем в таблицу 2 и проверяем выполнение равенства
.
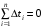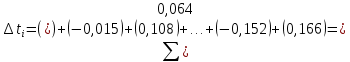0.Вычисляем значения
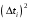и сумму 
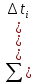. Результаты записываем в таблицу 2.Среднеквадратичная погрешность отдельного результата наблюдения:
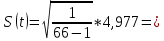0,617 сСреднеквадратичная погрешность среднего арифметического результата измерений:
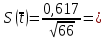0,759 сВычисляем случайную погрешность: (для нашего количества измерений при доверительной вероятности Р = 0,95, коэффициент Стьюдента
= 1,96.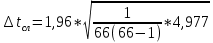
= 0,034 с Приборная погрешность электронного секундомера ∆х прибора = 0,001с. Она меньше случайной более чем в два раза. Тогда доверительную погрешность результата измерений приравниваем к случайной: ∆t = tсл= 0,034
Окончательный результат измерений: t = 4,977 ± 0,034 с; P = 0,95.
-
Оценим параметры закона распределения вероятностей с помощью гистограммы
По результатам измерений: tmax =5,258 с; tmin = 4,166 с, тогда ширина интервала:
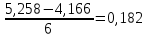с.Разобьем массив по ячейкам и результат занесем в таблицу 3.
Таблица 3 – Массив данных
| № | tmin | tmax | Δn | Δn/n |
| 1 | 4,166 | 4,348 | 1 | 0,015 |
| 2 | 4,348 | 4,530 | 0 | 0 |
| 3 | 4,530 | 4,712 | 2 | 0,030 |
| 4 | 4,712 | 4,894 | 13 | 0,20 |
| 5 | 4,894 | 5,076 | 33 | 0,50 |
| 6 | 5,076 | 5,258 | 17 | 0,26 |
;
;
;
;
;
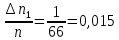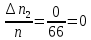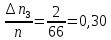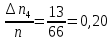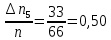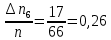
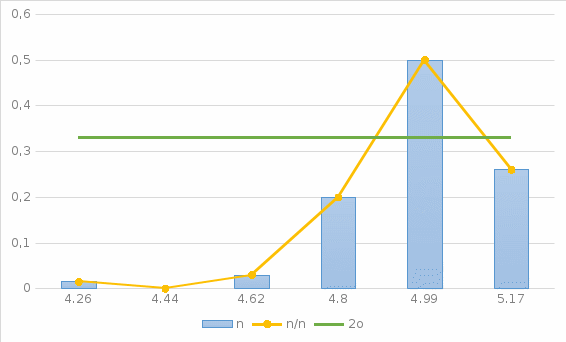
Приступаем к построению гистограммы экспериментальных значений и кривой закона распределения:
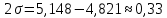, тогда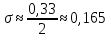 
Сравним величину
со значением σ, полученным при построении гистограммы и кривой закона распределения: = 0,617, а σ = 0,165. Из этого сравнения видно, что расчетное значение более чем в 4 раза больше чем найденное значение σ.Вывод: при выполнении данной лабораторной работы мною были получены практические навыки в освоении алгоритма обработки результатов прямых многократных прямых измерений, построена гистограммы экспериментальных значений определяемой величины и произведена оценка параметров распределения Гаусса из кривой закона распределения. По данной оценке можно сделать вывод, что расчетное значение
= 0,617 более чем в 4 раза превышает найденное по гистограмме σ = 0,165. Возможно, такое расхождение получилось из–за некорректные работы оператора, снимающего показания.Список литературы
1. Зайдель А. Н. Ошибки измерений физических величин: учеб. пособие А. Н. Зайдель. – СПб.: Лань, 2005. – 112 с.
2. Деденко Л. Г. Математическая обработка и оформление результатов эксперимента / Л. Г. Деденко, В. В. Керженцев. – М.: МГУ, 1977.
3. Измерения физических величин и обработка результатов измерений: метод. указания к лабораторной работе № 100. – СПб., 2000. – 30 с.
4. Руководство к лабораторным занятиям по физике / Под ред. Л. Л. Гольдина. – М.: Наука, 1973.