ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 111
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
09.03.03 Прикладная информатика
Физика
Лабораторная работа 1
На тему: "Механические колебания"
Выполнил : студент 1 курса
Проверил :
Профессор
1.Цель работы: Изучение механических колебаний.
2. Задачи : Приобретение навыков проведения физических измерений, умения обработки полученных данных.
3.Теоретическая часть:
Колебания механических систем, или механические колебания - это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия - это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Пружинный маятник - это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими. Груз имеет массу m, жёсткость пружины равна k.
Координате x=0 отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
Закон Гука — утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком.
Закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между силой и деформацией становится нелинейной.
F= -kx,
где
F- сила упругости [H]
k- коэффициент жесткости [H/m]
x- изменение длинны (деформация) [m]
В вертикальном направлении на груз действует только сила упругости F со стороны пружины. Ньютон установил связь между ускорением и силой, где F – сила, действующая на тело массой m, вызывает ускорение тела равное – a. Второй закон Ньютона для груза в проекции на ось x имеет вид:
F=ma
где
m — масса материальной точки
a — ускорение тела
F— сила действующая на тело/ускорение материальной точки
Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение, причем направления силы и ускорения совпадают.
Если на тело действует сила, то оно приобретает ускорение.
Ускорение, приобретаемое материальной точкой :
-
Прямо пропорционально действующей на точку силе; -
Обратно пропорционально массе точки; -
Направлено в сторону действия силы.
Перемещение – изменение положения тела в пространстве с течением времени .
Скорость векторная величина, характеризующая быстроту перемещения.4.Экспериментальная часть
Для работы нам потребуется следующее: штатив, соотвеисивующая измерительная установка – система координат, груз массой в 32 грамма, пружина, а также смартфон для фиксации движения груза на пружине. Работа выполняется на установке. Установка представляет собой стойку, состоящую из основания и несущей штанги, на которой крепятся кронштейн с прикрепленной к нему пружиной, к пружине прикреплен груз, к штанге прикреплена миллиметровая шкала.
Выводим пружинный маятник из положения равновесия
на 20 мм, чтобы придать ему ускорение и измеряем время 20 колебаний. Настраиваем смартфон в режим видеосъемки с 60 кадрами в секунду и фиксируем показания. После фиксации разбиваем видео на кадры и привязываем каждый кадр по времени положению грузика на координатной плоскости. (Фото.1)
Фото. 1 Полоение грузика относительно оси координат.
Исходя из полученных данных , выполняем расчеты :
| Время (t) | Положение груза по x | Δt | Δx | Скорость (V) | ΔV | a | Eк | Еп |
| 0 | 0 | | | | | | 0 | 0 |
| 1 | 4 | 1 | 4 | 4,0 | | | 256 | 1254,4 |
| 2 | -2 | 1 | -6 | -1,0 | -5 | -5 | 16 | -627,2 |
| 3 | 2 | 1 | 4 | 0,7 | 1,7 | 1,7 | 7,1 | 627,2 |
| 4 | -4 | 1 | -6 | -1,0 | -1,7 | -1,7 | 16 | -1254,4 |
| 5 | -6 | 1 | -2 | -1,2 | -0,2 | -0,2 | 23 | -1881,6 |
| 6 | 3 | 1 | 9 | 0,5 | 1,7 | 1,7 | 4 | 940,8 |
| 7 | 2 | 1 | -1 | 0,3 | -0,2 | -0,2 | 1,3 | 627,2 |
| 8 | 1 | 1 | -1 | 0,1 | -0,2 | -0,2 | 0,3 | 313,6 |
| 9 | -1 | 1 | -2 | -0,1 | -0,2 | -0,2 | 0,2 | -313,6 |
| 10 | 4 | 1 | 5 | 0,4 | 0,5 | 0,5 | 2,6 | 1254,4 |
| 11 | 1 | 1 | -3 | 0,1 | -0,3 | -0,3 | 0,1 | 313,6 |
| 12 | -2 | 1 | -3 | -0,2 | -0,3 | -0,3 | 0,4 | -627,2 |
| 13 | 5 | 1 | 7 | 0,4 | 0,6 | 0,6 | 2,4 | 1568 |
| 14 | -3 | 1 | -8 | -0,2 | -0,6 | -0,6 | 0,7 | -940,8 |
| 15 | 4 | 1 | 7 | 0,3 | 0,5 | 0,5 | 1,1 | 1254,4 |
| 16 | -2 | 1 | -6 | -0,1 | -0,4 | -0,4 | 0,3 | -627,2 |
| 17 | 1 | 1 | 3 | 0,1 | 0,2 | 0,2 | 0,1 | 313,6 |
| 18 | 2 | 1 | 1 | 0,1 | 0,1 | 0,1 | 0,2 | 627,2 |
| 19 | -1 | 1 | -3 | -0,1 | -0,2 | -0,2 | 0,04 | -313,6 |
| 20 | 4 | 1 | 5 | 0,2 | 0,3 | 0,3 | 0,6 | 1254,4 |
и получаем следующие графики (Рисунки 1-4)
Рис. 1 График потенциальной энергии.
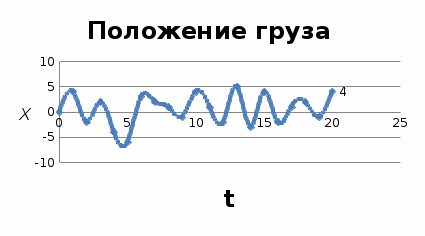Рис. 2 График положения груза на оси координат
Рис. 3 График кинетической энергии.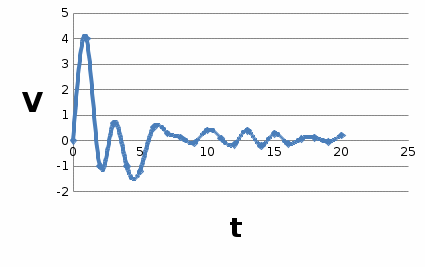
Рис.4 График изменения скорости.Вывод : проделав данную лабораторную работу и проведя проделанные исследования я увидела, как меняется кинетическая энергия и потенциальная энергия груза в зависимости от того, как меняется его положение в пространстве вследствие уменьшения скорости собственных колебаний.
Список литературы
1. Савельев И. В. Курс физики. Т. 2. – СПб.: Издательство «Лань», 2016.
2. Детлаф А. Н., Яворский Б. М. Курс физики. – М.: Academia, 2015.
3. Трофимова Т. И. Курс физики. – М.: Academia, 2016.