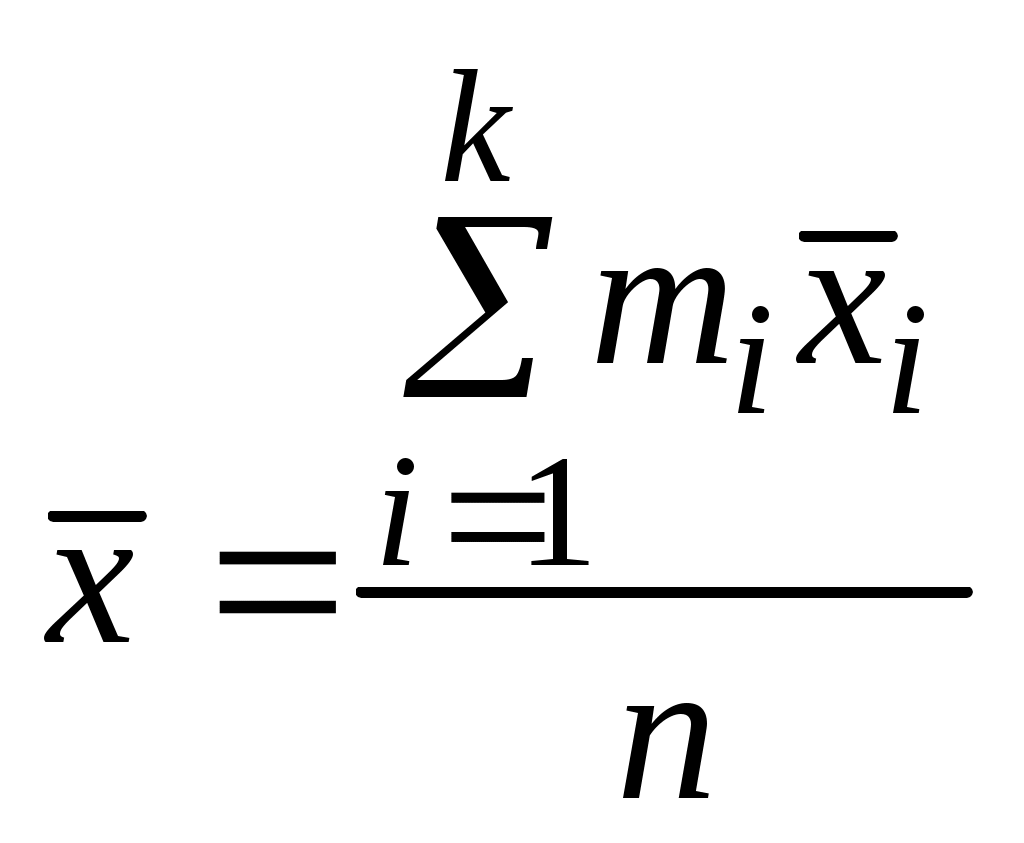Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 153
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Ивановский государственный энергетический
университет имени В.И. Ленина»
Кафедра тепловых электрических станций
Инженерные методы обработки результатов эксперимента
Методические указания к лабораторным работам
для студентов специальности 140101
«Тепловые электрические станции»
Иваново 2007
Составители: С.И. Шувалов
А.А. Андреев
Редактор А. В. Мошкарин
В методических указаниях изложены основные сведения о статистической обработке результатов эксперимента, представлены варианты индивидуальных заданий на лабораторные работы, приведены варианты их выполнения.
Методические указания к лабораторным работам для студентов специальности 140101 «Тепловые электрические станции» разработаны на основе ГОС (2004 г.).
Утверждены цикловой методической комиссией ТЭФ
Рецензент: кафедра тепловых электрических станций ИГЭУ
Вниманию студентов
Данные методические указания предназначены для выполнения лабораторных работ по курсу «Инженерные методы обработки результатов эксперимента» с помощью электронных таблиц Excel.
Исходные данные для лабораторной работы №1 формируются с помощью генератора случайных чисел, лабораторная работа №2 выполняется по данным работы №1, исходные данные для работ №3,4,5 представлены в приложении 1. Номер варианта задается преподавателем.
Статистические таблицы, необходимые для выполнения задания, приведены в приложении 2.
Лабораторная работа №1
Исследование распределения случайных величин на основе опытных данных
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем заранее неизвестно, какое именно. Признаком случайной величины является то, что при повторении опытов при видимых неизменных условиях получаются несколько различающиеся результаты. Отсюда следует, что представление результатов измерений случайной величины в виде единственного числа дает мало информации об истинных характеристиках исследуемого процесса.
Наиболее полной характеристикой случайной величины является закон распределения, связывающий возможное значение величины с вероятностью появления этого значения. Закон распределения может быть представлен или в виде таблицы, в которой указываются все возможные значения и соответствующие им вероятности, или в виде интегральной характеристики – функции распределения
F(x), или дифференциальной характеристики (только для непрерывных величин) – плотности распределения f(x). Функция и плотность распределения относятся к теоретическим характеристикам и могут быть точно определены по данным генеральной совокупности.
В действительности мы всегда имеем дело с ограниченным числом наблюдений, представляющих отдельные реализации случайной величины и образующих выборочную совокупность. Характеристики выборочной совокупности представляют приближенную оценку характеристик генеральной совокупности и могут несколько отличаться от характеристик генеральной совокупности.
Опытные данные, полученные в результате эксперимента, представляют собой первичный статистический материал, подлежащий обработке и анализу. Эта совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». Обычно простая статистическая совокупность оформляется в виде таблицы, в первом столбце которой стоит номер опыта, а во втором – наблюдаемое значение случайной величины. Если порядок проведения опытов не имеет принципиального значения, то более удобно поместить в таблицу значения случайной величины не в порядке их появления, а разместить по возрастанию, т.е. на первое место поставить наименьшее, а на последнее – наибольшее значение. Такой ряд называется упорядоченным.
Более информативным является представление опытных данных в виде функции распределения. По аналогии с теорией вероятности статистической функцией распределения F*(хi) случайной величины X называется частота события появления значений величины X<xi:
Для того чтобы найти значение статистической функции распределения при данном xi, необходимо подсчитать число опытов, в которых случайная величина X приняла значение, меньшее, чем xi, и разделить это количество на общее число произведенных опытов.
Статистическая функция распределения любой случайной величины (прерывной или непрерывной) представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюдаемым значениям случайной величины и по величине равны частотам этих значений. Если каждое отдельное значение случайной величины наблюдалось только один раз, то скачок статистической функции распределения в каждом наблюденном значении будет равен 1/
n, где
n – число наблюдений.
Согласно теореме Бернулли при увеличении числа опытов n частота события X < xi для любого xi сходится по вероятности к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения будет приближаться к подлинной функции распределения F(хi) случайной величины Х. Если X – непрерывная случайная величина, то при увеличении числа наблюдений n число скачков функции F*(хi) будет увеличиваться, а сами скачки уменьшаться. График функции F*(хi) приблизится к плавной кривой F(x).
При большом числе наблюдений простая статистическая совокупность становится слишком громоздкой, поэтому на основании первичных наблюдений строится так называемый «статистический ряд». Для этого весь диапазон полученных значений сначала X разбивается на k интервалов. Число интервалов, на которых группируется статистический материал, не должно быть ни слишком большим (тогда частоты будут случайным образом колебаться), ни слишком малым, чтобы не было слишком грубой оценки. Обычно ограничиваются количеством интервалов k = 10…20. Длины интервалов могут быть одинаковыми или различными. Если плотность распределения очень неравномерна, то удобно выбирать в области высокой плотности более узкие интервалы, а в области низкой плотности – более широкие.
Далее подсчитывается количество значений mi случайной величины X, попавших в каждый i-й интервал. При группировке значения величины X, попавшие точно на границы интервала, относят с половиной частоты попадания в каждый сопряженный интервал, наименьшее и наибольшее значения относят полностью соответственно в первый и последний интервалы. Сумма попаданий во все интервалы должна быть точно равна количеству результатов:
При группировке значений по интервалам принимается, что случайная величина, попавшая в i-й интервал, приняла значение, равное среднему арифметическому границ интервала:
Частота попаданий величины в каждый из интервалов вычисляется по формуле
Сумма частот всех разрядов равна единице:
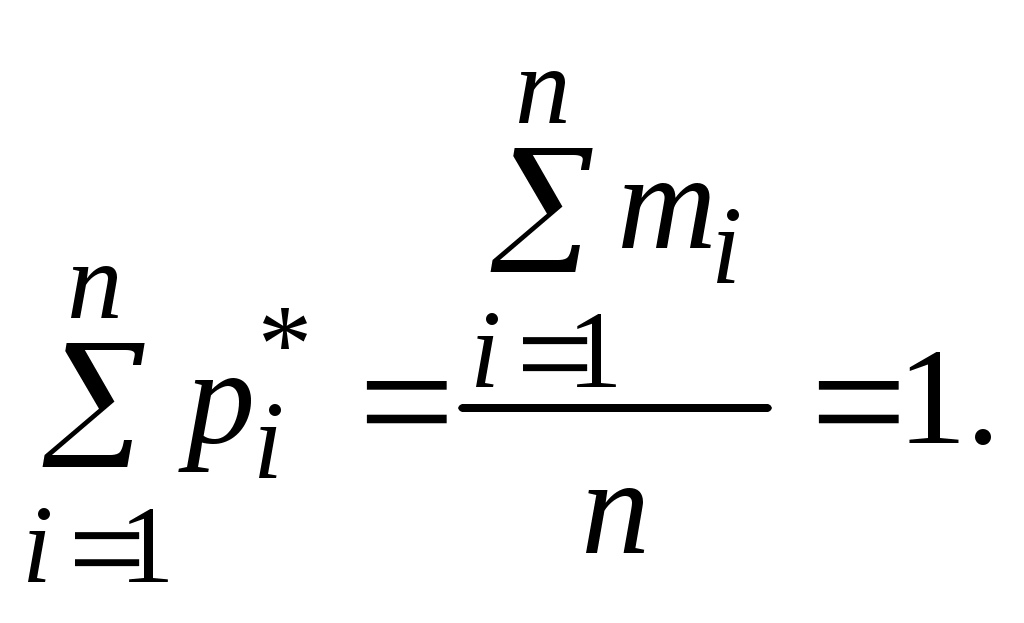 (1.4)
(1.4)Таблица, в которой приведены разряды в порядке их расположения вдоль оси X и соответствующие им частоты, называется статистическим рядом (табл. 1.1).
Таблица 1.1 Общий вид статистического ряда в табличной форме
| № интервала | 1 | 2 | | i | | k |
| Ширина интервала | x1…x2 | x2…x3 | | xi…xi+1 | | xk…xk+1 |
| Среднее значение | | | | | | |
| Частота попадания в интервал | | | | | | |
Частота попаданий случайной величины в интервал является приближенной оценкой вероятности попадания величины в этот интервал. По полученным данным можно построить график статистической функции распределения величины Х.
Согласно принятым допущениям в опытах не наблюдались значения менее
происходит скачок функции распределения на величину
В ряде случаев более наглядным и удобным является описание случайной величины с помощью плотности распределения, аналогом которой для опытных данных является гистограмма распределения. Следует отметить, что если плотность распределения существует только для непрерывных случайных величин, то гистограмму можно построить также и для дискретных величин.
Гистограмма строится следующим образом. На оси абсцисс наносятся границы интервалов, и на этих интервалах строятся прямоугольники, площадь которых равна частоте попадания случайной величины в данный интервал. Высота прямоугольников рассчитывается по формуле
В тех случаях, когда не требуется полной информации о законе распределения случайной величины, бывает достаточно ограничиться некоторыми численными характеристиками. По аналогии с теорией вероятности в математической статистике для представления о поведении случайной величины наиболее часто применяются характеристика положения (среднее арифметическое – аналог математическому ожиданию) и характеристики разброса значений случайной величины относительного среднего положения (выборочные дисперсия и среднеквадратичное отклонение – аналоги дисперсии и среднеквадратичного отклонения генеральной совокупности).
Среднее арифметическое наблюдаемой величины рассчитывается по формуле