Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 154
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. (1.6)
Выборочные дисперсия и среднеквадратичные отклонения рассчитываются по формулам:
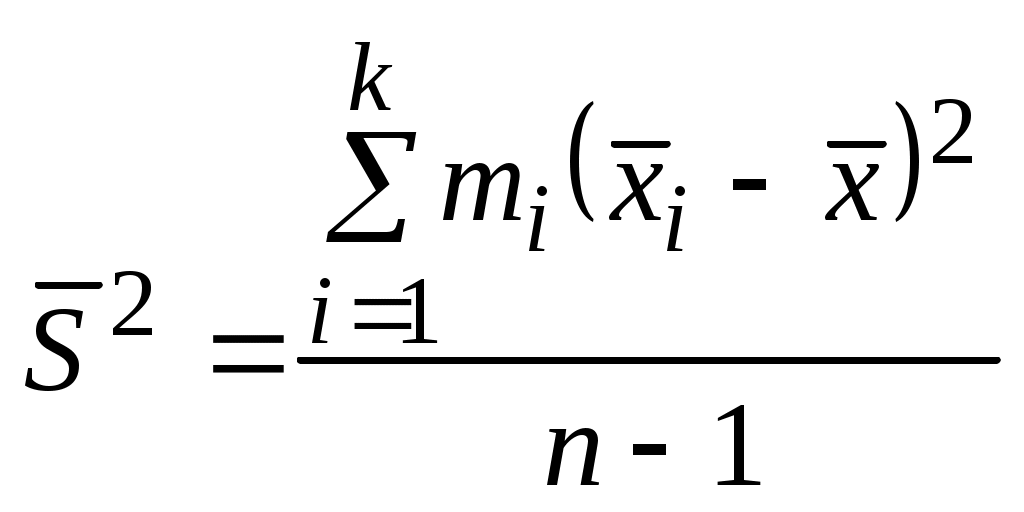, (1.7)
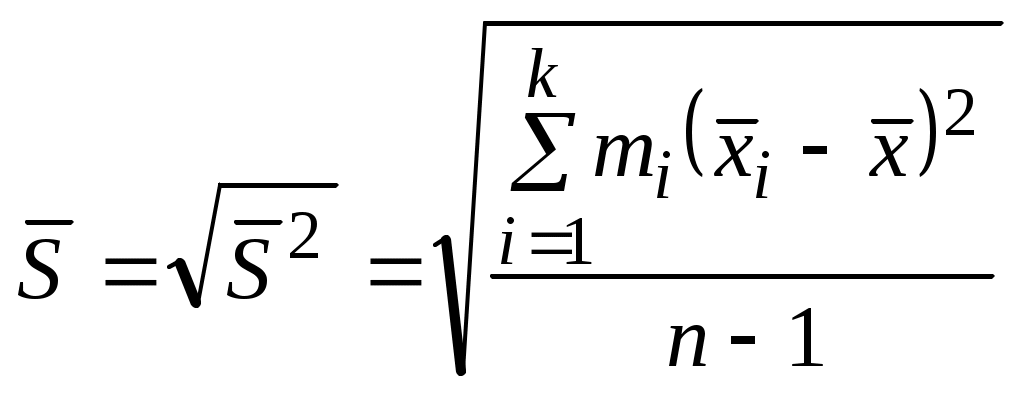. (1.8)
Задание на лабораторную работу
С помощью генератора случайных чисел сформировать массив из 60 чисел, распределенных по нормальному закону с параметрами m=5 и =10. Разделить диапазон изменения значений чисел на 10 интервалов, распределить числа по интервалам. Для сгруппированных данных построить график функции распределения и гистограмму плотности распределения, вычислить среднее арифметическое, дисперсию и среднеквадратичное отклонение. Все расчеты и графики выполнить с помощью электронных таблиц EXCEL.
Пример выполнения лабораторной работы
Формирование массива данных
Электронные таблицы EXCEL содержат встроенную функцию СЛЧИС, при обращении к которой генерируется случайное число, равномерно распределенное в интервале [0, 1]. Для того чтобы получить нормальное распределение, воспользуемся зависимостью
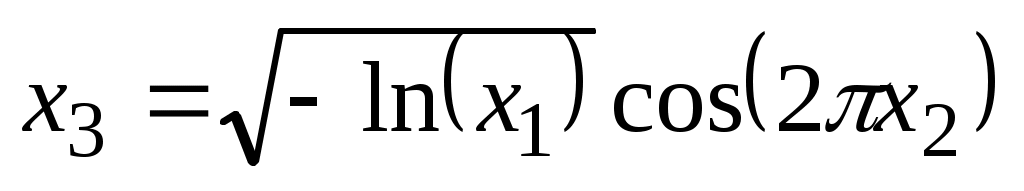. (1.9)
Здесь х3 – случайное число, обладающее нормальным распределением в диапазоне [0, 1]; х1, х2 – случайные числа, равномерно распределенные в этом же диапазоне. Выражение (1.9) будем использовать в виде
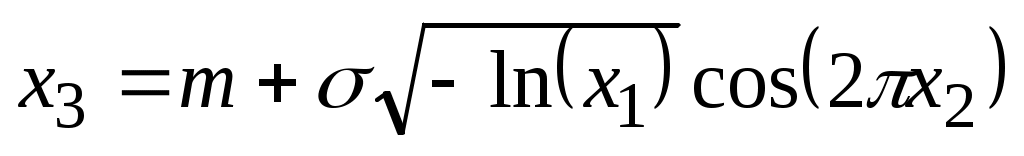, (1.10)
обеспечивающем генерацию случайных чисел, распределенных по нормальному закону с параметрами m и .
Откроем программу MicrosoftExcel и выберем рабочий лист, предназначенный для выполнения данной лабораторной работы. Для того чтобы при последующем обращении к документу было ясно, какая информация содержится на данном рабочем листе, активизируем ячейку А1 и запишем заголовок Лабораторная работа №1. Затем в ячейках А3:С3 укажем заголовки столбцов таблицы исходных данных №, х1, х2. Далее в ячейки А4:А63 введем порядковые номера случайных величин от 1 до 60, т.е. заполним первый столбик таблицы.
Активизируем ячейку В4. Из меню Вставка в главном меню выберем команду Функция или на панели инструментов щелкнем по значку
. Появится окно Мастера функций. Из категории Математические выберем функцию СЛЧИС, которая задает случайное число. После нажатия клавиши ОК в ячейке В4 появится случайное число между 0 и 1. Растянем ячейку В4 до ячейки В63 и затем до С63. В результате этих операций в столбцах В и С получим случайные числа, равномерно распределенные между 0 и 1.
Обратите внимание, что при вводе новых случайных чисел ранее введенные величины меняют свое значение. Чтобы зафиксировать значения случайных чисел, выполним следующие операции:
После этих операций в ячейках F4:G63 появится новая таблица с зафиксированными значениями случайных чисел.
Приступим к формированию массива случайных чисел, распределенных по нормальному закону. В ячейке Н3 запишем заголовок столбца х3, а в ячейках А65 и А66 имена параметров m= и сигма=.В ячейки В65 и В66 введем значения параметров соответственно 5 и 10.
Активизируем ячейку Н4 и введем в нее формулу (1.10) в виде
=$B$65+$B$66*КОРЕНЬ(-LN(F4))*COS(2*ПИ()*G4)
Следует обратить внимание на следующие особенности записи:
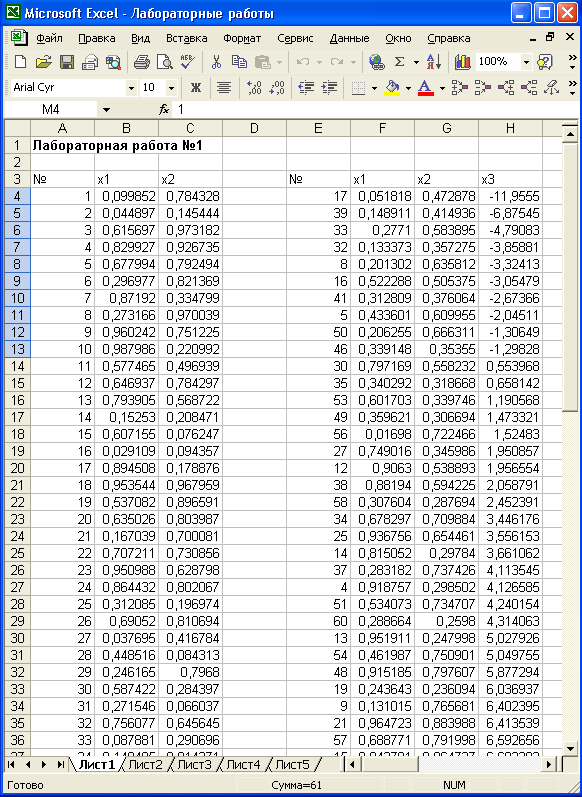
После ввода формулы растянем ячейку Н4 до Н63, в результате чего получим требуемый массив чисел. Общий вид листа с таблицей исходных данных показан на рис.1.1.
Рис. 1.1. Общий вид таблицы исходных данных
Группировка данных по интервалам
Чтобы разделить исходные данные по интервалам, их необходимо сначала расставить в порядке возрастания значений. Для этого выделим диапазон значений Н4:Н63 и воспользуемся иконкой
панели инструментов. Сортировку также можно производить с помощью команды Сортровка в меню Данные главного меню.
После сортировки в нашем случае на первом месте оказалось число -11,955, на последнем – число 17,77649. Примем с небольшим запасом, что все наблюдаемые значения случайной величины находятся внутри диапазона [-12, 18].
Разделим этот диапазон на 10 равных по длине интервалов. Для группировки и обработки данных составим новую таблицу. В ячейки J3:P3 запишем заголовки столбцов: №, x (номер границы диапазона), xcp (среднее значение случайной величины внутри диапазона), m (количество попаданий величины в дианазон), р (частота попаданий), F (значение статичтической функции распределения),h (высота прямоугольников гистограммы).
Далее в ячейки J4:J14 введем номера границ интервалов от 1 до 11, а в ячейки K4:K14 границы интервалов. В ячейках L4:L13 запишем средние значения случайной величины внутри интервала. Для этого активизируем ячейку L4, введем туда формулу =(K4+K5)/2 и растянем эту ячейку до L13.
В ряду Н4:Н63 подсчитаем количество попаданий случайной величины в каждый интервал и занесем результаты в ячейки М4:М13. Для контроля расчета вычислим сумму попаданий, для чего выделим ячейки М4:М13 и на панели инструментов щелкнем мышкой по иконке . Результат суммирования, который появится в ячейке М14, должен быть равен количеству значений случайной величины. Для нашего случая там должно быть число 60.
В ячейках N4:N13 подсчитаем частоту попаданий случайной величины в интервалы, для чего активизируем ячейку N4, запишем в нее формулу =M4/$M$14 и растянем ячейку до N13. Сумма частот, приведенная в ячейке N14, должна быть точно равна 1.
В ячейках О4:О13 вычислим значение статистической функции распределения случайной величины. Внутри каждого интервала при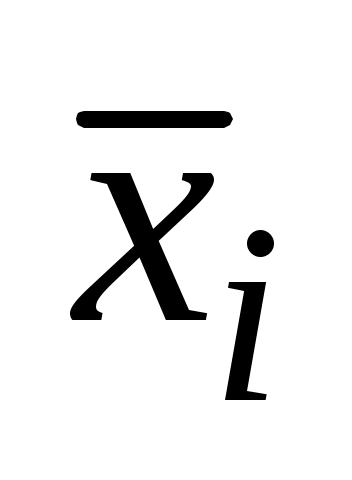
происходит скачок функции распределения на величину, равную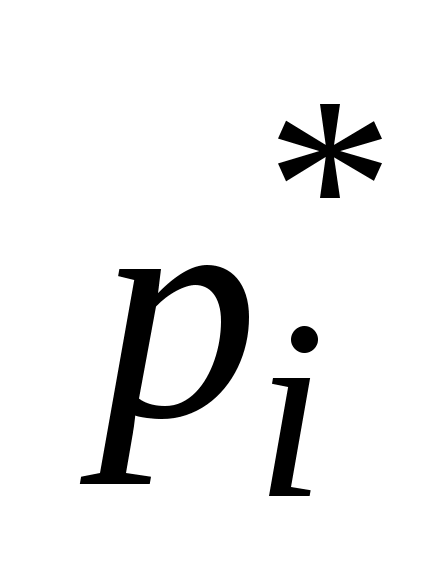 
. Условимся записывать в ячейки значения функции распределения после скачка. Для этого в ячейку О4 запишем данные ячейки N4, в ячейку О5 введем формулу =O4+N5 и растянем эту ячейку до О13.
В ячейках Р4:Р13 вычислим высоты прямоугольников для гистограммы плотности распределения случайной величины. Активизируем ячейку Р4, запишем туда формулу =N4/(K5-K4) и растянем ячейку до Р13.
Массив данных J3:P14 представляет собой статистический ряд, дополненный значениями статистической функции распределения и высот прямоугольников для гистограммы. Общий вид статистического ряда для наших исходных данных представлен на рис.1.2.
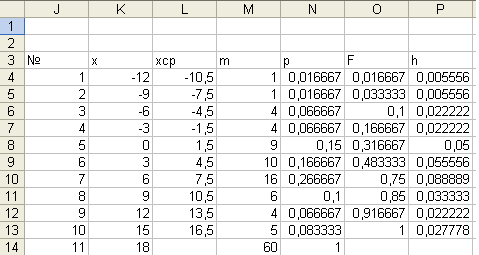
Рис. 1.2. Общий вид статистического ряда
Построение графиков функции и гистограммы распределения
Для построения графиков и диаграмм EXCEL использует подпрограмму Мастер диаграмм, вызываемую пиктограммой
на панели инструментов. Мастер диаграмм располагает набором из девяти плоских и шести объемных типов диаграмм, каждая из которых имеет еще несколько вариантов. Для нашей задачи необходимо взять плоскую диаграмму типа Точечная, которая строит графики по координатам точек, указанных в двух рядах данных.
Для построения графика функции распределения построим ряды данных следующим образом. В ячейки U3 и V3 запишем заголовки столбцов соответственно x и F. На основании принятых при группировке данных допущений в опытах не наблюдалось появление значений случайной величины менее среднего арифметического границ первого интервала. Поэтому до этого значения функция распределения должна быть равной нулю. Этот факт графически изображается прямой линией, проведенной по оси абсцисс до середины первого интервала. Не имеет значения, с какой точки начать эту линию. Для определенности в качестве начальной точки возьмем начало первого интервала и запишем в ячейки U4 и V4 значения -12 и 0. Для завершения этой линии в ячейках U5 и V5 укажем координаты середины первого интервала, введя соответственно -10,5 и 0.
В этой точке функция распределения скачком увеличивается до 0,016667. Для изображения вертикальной прямой в ячейки U6 и V6 введем значения -10,5 и 0,016667. Продолжая эту процедуру, мы дойдем до середины последнего интервала, в которой функция распределения достигает максимального значения, равного единице. В нашем случае этой точке соответствуют координаты 16,5 и 1.
Для сгруппированных данных предполагается, что все наблюдаемые значения меньше середины последнего интервала. Поэтому для всех значений, больше этой величины, функция распределения остается постоянной и равной единице. Проведем эту линию до конца последнего интервала, для чего запишем в последнюю строчку ряда U25 и V25 координаты 18 и 1.
Аналогичным образом строим ряды данных для построения гистограммы. Вид рядов на листе EXCEL показан на рис.1.3.
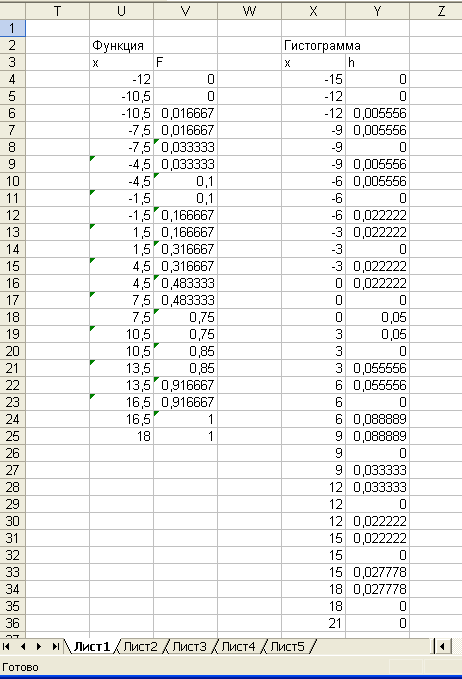
Рис. 1.3. Исходные данные для построения диаграммы типа Точечная
Для построения графика функции распределения необходимо выделить массив U4:V25, щелкнуть мышкой по пиктограмме
, выбрать тип диаграммы Точечная, выбрать вид рисования прямыми линиями без маркеров, нажать кнопку Готово и переместить появившийся на экране график на свободное место.
После настройки изображения (корректировка размеров графика, заливки области построения, шкал, толщины линий, подписи осей и заголовка) строится гистограмма распределения. Рекомендуется располагать один график под другим таким образом, чтобы оси случайной величины х соответствовали друг другу. В этом случае достаточно легко сопоставить информацию, получаемую с одного и другого графиков. Окончательный вид графиков функции распределения и гистограммы показан на рис. 1.4, 1.5.
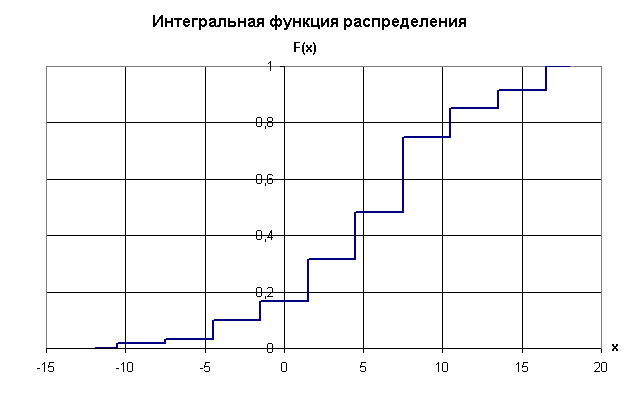
Рис. 1.4. График функции распределения
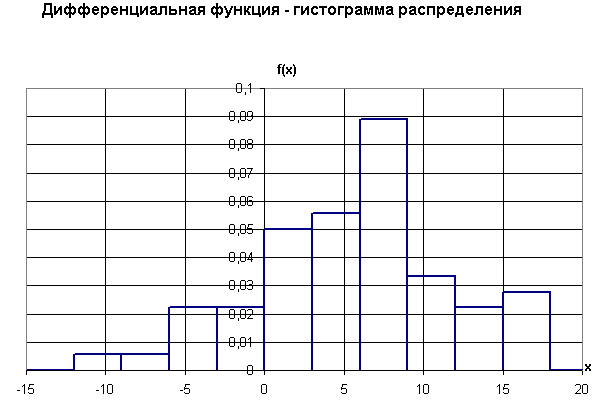
Рис. 1.5. Гистограмма распределения
Расчет численных характеристик распределения
Для расчета среднего арифметического и дисперсии по формулам (1.6) и (1.7) необходимо вычислить суммы произведений:
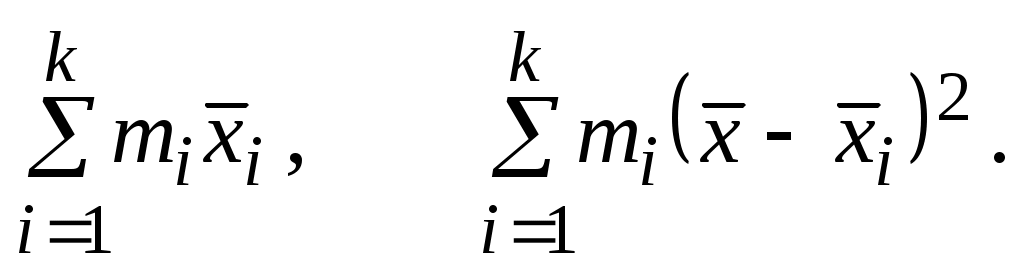
Запишем в ячейки R3 и S3 заголовки столбцов mx и m(x-xcp)^2. Затем в ячейку R4 введем формулу =L4*M4, а в ячейку S4 – формулу =M4*(L4-$R$15)^2, затем растянем ячейки до R13 и S13. В ячейках R14 и S14 подсчитаем соответствующие суммы, а в ячейках R15, S16 и S17 – соответственно среднее арифметическое, дисперсию и среднеквадратическое отклонение. Общий вид таблицы с расчетом этих параметров показан на рис.1.6.
На этом лабораторная работа №1 завершена.
Выборочные дисперсия и среднеквадратичные отклонения рассчитываются по формулам:
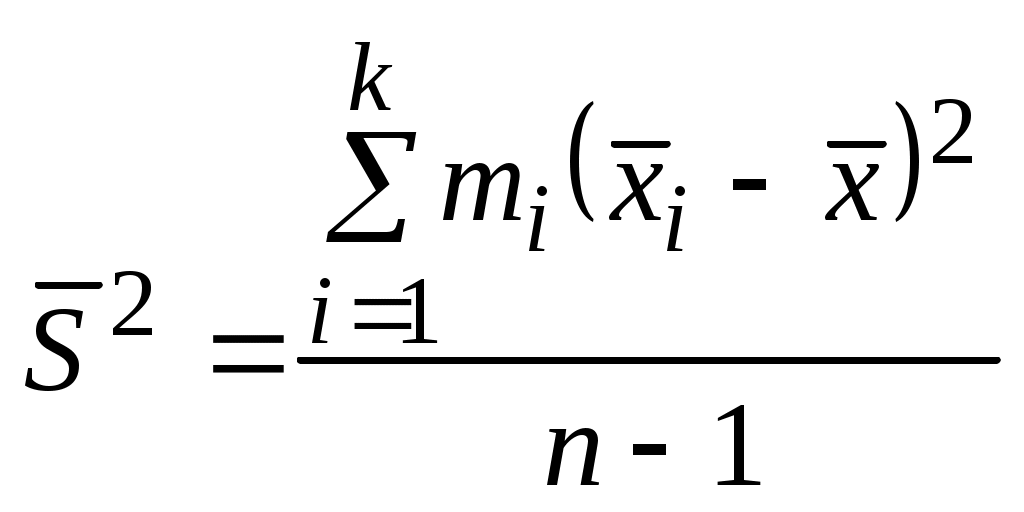, (1.7) 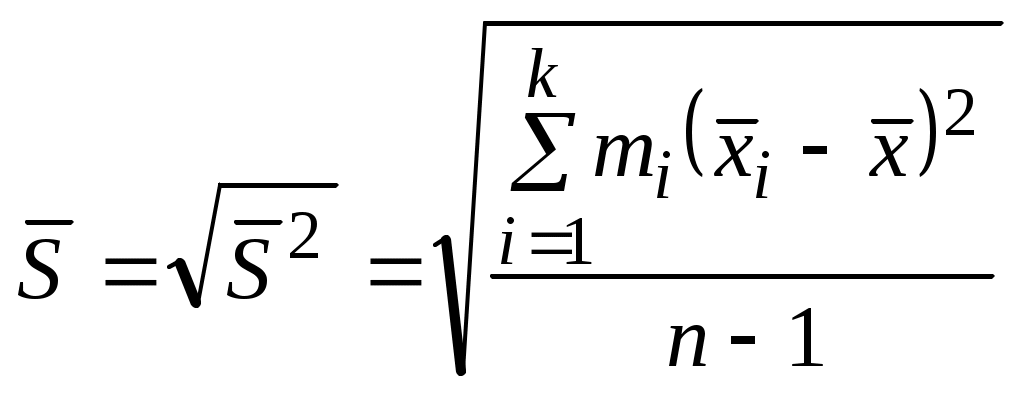. (1.8)Задание на лабораторную работу
С помощью генератора случайных чисел сформировать массив из 60 чисел, распределенных по нормальному закону с параметрами m=5 и =10. Разделить диапазон изменения значений чисел на 10 интервалов, распределить числа по интервалам. Для сгруппированных данных построить график функции распределения и гистограмму плотности распределения, вычислить среднее арифметическое, дисперсию и среднеквадратичное отклонение. Все расчеты и графики выполнить с помощью электронных таблиц EXCEL.
Пример выполнения лабораторной работы
Формирование массива данных
Электронные таблицы EXCEL содержат встроенную функцию СЛЧИС, при обращении к которой генерируется случайное число, равномерно распределенное в интервале [0, 1]. Для того чтобы получить нормальное распределение, воспользуемся зависимостью
. (1.9)Здесь х3 – случайное число, обладающее нормальным распределением в диапазоне [0, 1]; х1, х2 – случайные числа, равномерно распределенные в этом же диапазоне. Выражение (1.9) будем использовать в виде
, (1.10)обеспечивающем генерацию случайных чисел, распределенных по нормальному закону с параметрами m и .
Откроем программу MicrosoftExcel и выберем рабочий лист, предназначенный для выполнения данной лабораторной работы. Для того чтобы при последующем обращении к документу было ясно, какая информация содержится на данном рабочем листе, активизируем ячейку А1 и запишем заголовок Лабораторная работа №1. Затем в ячейках А3:С3 укажем заголовки столбцов таблицы исходных данных №, х1, х2. Далее в ячейки А4:А63 введем порядковые номера случайных величин от 1 до 60, т.е. заполним первый столбик таблицы.
Активизируем ячейку В4. Из меню Вставка в главном меню выберем команду Функция или на панели инструментов щелкнем по значку
. Появится окно Мастера функций. Из категории Математические выберем функцию СЛЧИС, которая задает случайное число. После нажатия клавиши ОК в ячейке В4 появится случайное число между 0 и 1. Растянем ячейку В4 до ячейки В63 и затем до С63. В результате этих операций в столбцах В и С получим случайные числа, равномерно распределенные между 0 и 1.
Обратите внимание, что при вводе новых случайных чисел ранее введенные величины меняют свое значение. Чтобы зафиксировать значения случайных чисел, выполним следующие операции:
-
Выделим таблицу, т.е. диапазон ячеек А3:С63. -
Скопируем содержимое выделенного диапазона в буфер обмена. Для этого в меню Правка главного меню выберем команду Копировать. -
Активируем ячейку Е3 и с помощью команды Специальная вставка меню Правка вставим значения выделенного диапазона.
После этих операций в ячейках F4:G63 появится новая таблица с зафиксированными значениями случайных чисел.
Приступим к формированию массива случайных чисел, распределенных по нормальному закону. В ячейке Н3 запишем заголовок столбца х3, а в ячейках А65 и А66 имена параметров m= и сигма=.В ячейки В65 и В66 введем значения параметров соответственно 5 и 10.
Активизируем ячейку Н4 и введем в нее формулу (1.10) в виде
=$B$65+$B$66*КОРЕНЬ(-LN(F4))*COS(2*ПИ()*G4)
Следует обратить внимание на следующие особенности записи:
-
ввод формулы начинается со знака «=»; -
при ссылке на параметры указываются адреса ячеек, где хранятся значения параметров, а не их имена; в частности, здесь указаны ячейки В65 и В66, а не А65 и А66; -
так как при пересчете значений случайной величины для других ячеек значения параметров должны оставаться постоянными, а значения величин х1 и х2 должны меняться соответственно каждой строке, то при вводе адреса параметров фиксируются, а адреса величин х1 и х2 указываются без фиксации; -
значение =3,14159… является встроенной функцией EXCEL;хотя эта функция параметров не имеет, при ее вводе после имени функции необходимо поставить открывающую и закрывающую круглые скобки.
После ввода формулы растянем ячейку Н4 до Н63, в результате чего получим требуемый массив чисел. Общий вид листа с таблицей исходных данных показан на рис.1.1.
Рис. 1.1. Общий вид таблицы исходных данных
Группировка данных по интервалам
Чтобы разделить исходные данные по интервалам, их необходимо сначала расставить в порядке возрастания значений. Для этого выделим диапазон значений Н4:Н63 и воспользуемся иконкой
панели инструментов. Сортировку также можно производить с помощью команды Сортровка в меню Данные главного меню.После сортировки в нашем случае на первом месте оказалось число -11,955, на последнем – число 17,77649. Примем с небольшим запасом, что все наблюдаемые значения случайной величины находятся внутри диапазона [-12, 18].
Разделим этот диапазон на 10 равных по длине интервалов. Для группировки и обработки данных составим новую таблицу. В ячейки J3:P3 запишем заголовки столбцов: №, x (номер границы диапазона), xcp (среднее значение случайной величины внутри диапазона), m (количество попаданий величины в дианазон), р (частота попаданий), F (значение статичтической функции распределения),h (высота прямоугольников гистограммы).
Далее в ячейки J4:J14 введем номера границ интервалов от 1 до 11, а в ячейки K4:K14 границы интервалов. В ячейках L4:L13 запишем средние значения случайной величины внутри интервала. Для этого активизируем ячейку L4, введем туда формулу =(K4+K5)/2 и растянем эту ячейку до L13.
В ряду Н4:Н63 подсчитаем количество попаданий случайной величины в каждый интервал и занесем результаты в ячейки М4:М13. Для контроля расчета вычислим сумму попаданий, для чего выделим ячейки М4:М13 и на панели инструментов щелкнем мышкой по иконке . Результат суммирования, который появится в ячейке М14, должен быть равен количеству значений случайной величины. Для нашего случая там должно быть число 60.
В ячейках N4:N13 подсчитаем частоту попаданий случайной величины в интервалы, для чего активизируем ячейку N4, запишем в нее формулу =M4/$M$14 и растянем ячейку до N13. Сумма частот, приведенная в ячейке N14, должна быть точно равна 1.
В ячейках О4:О13 вычислим значение статистической функции распределения случайной величины. Внутри каждого интервала при
происходит скачок функции распределения на величину, равную
. Условимся записывать в ячейки значения функции распределения после скачка. Для этого в ячейку О4 запишем данные ячейки N4, в ячейку О5 введем формулу =O4+N5 и растянем эту ячейку до О13.
В ячейках Р4:Р13 вычислим высоты прямоугольников для гистограммы плотности распределения случайной величины. Активизируем ячейку Р4, запишем туда формулу =N4/(K5-K4) и растянем ячейку до Р13.
Массив данных J3:P14 представляет собой статистический ряд, дополненный значениями статистической функции распределения и высот прямоугольников для гистограммы. Общий вид статистического ряда для наших исходных данных представлен на рис.1.2.
Рис. 1.2. Общий вид статистического ряда
Построение графиков функции и гистограммы распределения
Для построения графиков и диаграмм EXCEL использует подпрограмму Мастер диаграмм, вызываемую пиктограммой
на панели инструментов. Мастер диаграмм располагает набором из девяти плоских и шести объемных типов диаграмм, каждая из которых имеет еще несколько вариантов. Для нашей задачи необходимо взять плоскую диаграмму типа Точечная, которая строит графики по координатам точек, указанных в двух рядах данных. Для построения графика функции распределения построим ряды данных следующим образом. В ячейки U3 и V3 запишем заголовки столбцов соответственно x и F. На основании принятых при группировке данных допущений в опытах не наблюдалось появление значений случайной величины менее среднего арифметического границ первого интервала. Поэтому до этого значения функция распределения должна быть равной нулю. Этот факт графически изображается прямой линией, проведенной по оси абсцисс до середины первого интервала. Не имеет значения, с какой точки начать эту линию. Для определенности в качестве начальной точки возьмем начало первого интервала и запишем в ячейки U4 и V4 значения -12 и 0. Для завершения этой линии в ячейках U5 и V5 укажем координаты середины первого интервала, введя соответственно -10,5 и 0.
В этой точке функция распределения скачком увеличивается до 0,016667. Для изображения вертикальной прямой в ячейки U6 и V6 введем значения -10,5 и 0,016667. Продолжая эту процедуру, мы дойдем до середины последнего интервала, в которой функция распределения достигает максимального значения, равного единице. В нашем случае этой точке соответствуют координаты 16,5 и 1.
Для сгруппированных данных предполагается, что все наблюдаемые значения меньше середины последнего интервала. Поэтому для всех значений, больше этой величины, функция распределения остается постоянной и равной единице. Проведем эту линию до конца последнего интервала, для чего запишем в последнюю строчку ряда U25 и V25 координаты 18 и 1.
Аналогичным образом строим ряды данных для построения гистограммы. Вид рядов на листе EXCEL показан на рис.1.3.
Рис. 1.3. Исходные данные для построения диаграммы типа Точечная
Для построения графика функции распределения необходимо выделить массив U4:V25, щелкнуть мышкой по пиктограмме
, выбрать тип диаграммы Точечная, выбрать вид рисования прямыми линиями без маркеров, нажать кнопку Готово и переместить появившийся на экране график на свободное место. После настройки изображения (корректировка размеров графика, заливки области построения, шкал, толщины линий, подписи осей и заголовка) строится гистограмма распределения. Рекомендуется располагать один график под другим таким образом, чтобы оси случайной величины х соответствовали друг другу. В этом случае достаточно легко сопоставить информацию, получаемую с одного и другого графиков. Окончательный вид графиков функции распределения и гистограммы показан на рис. 1.4, 1.5.
Рис. 1.4. График функции распределения
Рис. 1.5. Гистограмма распределения
Расчет численных характеристик распределения
Для расчета среднего арифметического и дисперсии по формулам (1.6) и (1.7) необходимо вычислить суммы произведений:
Запишем в ячейки R3 и S3 заголовки столбцов mx и m(x-xcp)^2. Затем в ячейку R4 введем формулу =L4*M4, а в ячейку S4 – формулу =M4*(L4-$R$15)^2, затем растянем ячейки до R13 и S13. В ячейках R14 и S14 подсчитаем соответствующие суммы, а в ячейках R15, S16 и S17 – соответственно среднее арифметическое, дисперсию и среднеквадратическое отклонение. Общий вид таблицы с расчетом этих параметров показан на рис.1.6.
На этом лабораторная работа №1 завершена.