Файл: Методические указания к лабораторным работам для студентов специальности 140101.doc

Лабораторная работа №2

Проверка распределения статистических данных

по закону Гаусса
При обработке статистического материала приходится решать вопрос, как подобрать для данного статистического ряда теоретическую кривую распределения. Такая задача называется выравниванием или сглаживанием статистических рядов.

Аналитическое выражение для описания любого теоретического распределения содержит численные коэффициенты, с помощью которых можно изменять конкретный вид распределения и согласовывать теоретическое распределение с экспериментальными данными. Эти коэффициенты называются параметрами распределения.

Один из методов выбора коэффициентов заключается в следующем: параметры выбираются таким образом, чтобы наиболее важные числовые характеристики совпадали у теоретического и статистического распределений. Например, если теоретическое распределение имеет один параметр, то подбираются равными математическое ожидание теоретического распределения и среднее арифметическое экспериментальных данных; если два параметра, то должны совпадать математическое ожидание и дисперсия генеральной совокупности со средним арифметическим и выборочной дисперсией и т.д.

Во многих технических приложениях используется распределение Гаусса (нормальное распределение), плотность которого определяется выражением

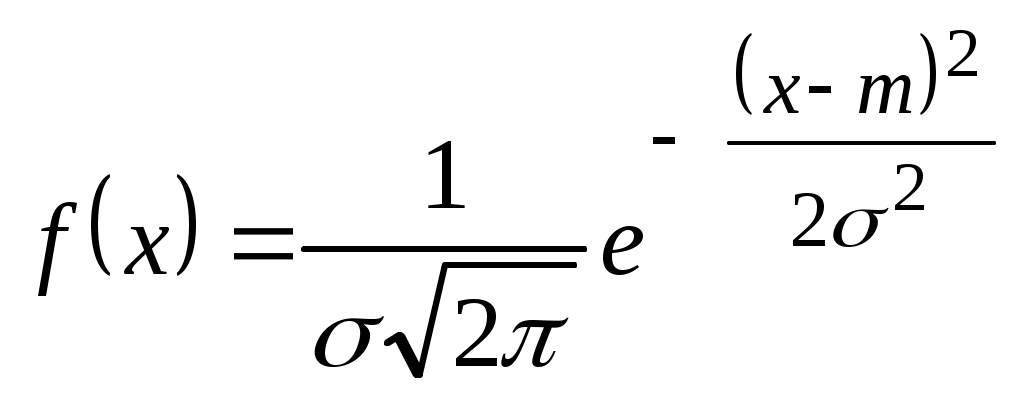. (2.1)

Распределение имеет два параметра: mи . Параметр m соответствует математическому ожиданию случайной величины, а  – среднеквадратическому отклонению генеральной совокупности.

На основании опытных данных можно рассчитать характеристики выборочной совокупности: среднее арифметическое и среднеквадратическое отклонение , являющиеся приближенной оценкой параметров генеральной совокупности. Тогда для расчета вероятности распределения случайной величины можно использовать (2.1) в виде

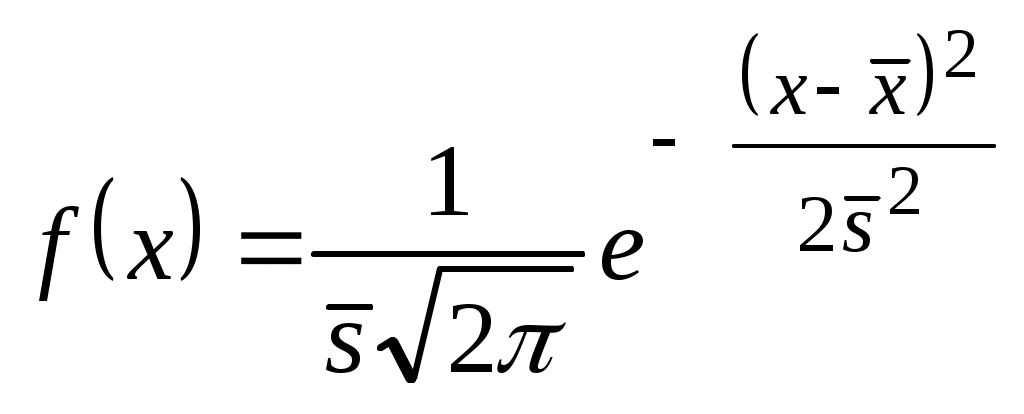. (2.2)

Однако простая замена mи  на и не гарантирует того, что теоретическое распределение будет соответствовать реально наблюдаемому. Проверка соответствия проводится следующим образом. Предположим, что произведено

---

n опытов, в каждом из которых случайная величина Х приняла определенное значение. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда:

№	1	2	…	i	…	k
xmin	x1,min	x2,min		xi,min		xk,min
xmax	x1,max	x2,max		xi,max		Xk,max
m	m1	m2		mi		mk

Требуется проверить, согласуются ли экспериментальные данные с тем, что случайная величина Х имеет закон распределения, заданный функцией распределения F(x) или плотностью распределения f(x).

На основании опытных данных можно по (1.3) вычислить частоту попадания случайной величины в каждый из интервалов р^*_i. Зная теоретический закон распределения, можно найти вероятности попадания случайной величины в каждый из интервалов p₁, p₂,…, p_k. Частота попаданий является приближенной оценкой вероятности, поэтому при правильном выборе теоретического закона для описания реального процесса разница между этими величинами будет невелика. В том случае, если исследуемая случайная величина имеет принципиально другое распределение, различия между частотами и вероятностями будут существенными.

В качестве количественной оценки соответствия теоретического и экспериментального законов распределения возьмем сумму квадратов разностей частот и вероятностей, взятых с некоторыми весовыми коэффициентами:

(2.3)

Коэффициенты c_i вводятся потому, что в общем случае отклонения, относящиеся к различным разрядам, нельзя считать равноценными по значимости. Одно и то же по абсолютной величине отклонение можно считать малым, если значение

---

p_i велико, или очень большим, если p_i мало.

Пирсон показал, что если взять , то при больших n закон распределения величины U практически не зависит от функции распределения F(x) и от числа опытов n, а будет определяться только числом разрядов k. Выражение (2.3) принимает вид

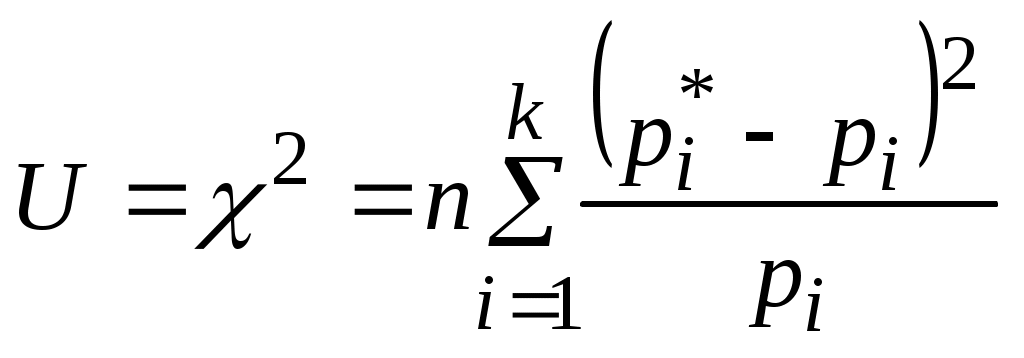. (2.4)

Сама функция в этом случае обозначается как U= ² и называется «хи-квадрат критерий Пирсона». Для удобства вычислений (2.4) приводят к виду

. (2.5)

Здесь m_i – количество попаданий случайной величины в i-й интервал.

При увеличении n закон распределения ² приближается к предельному распределению, которое зависит только от параметра , называемого «числом степеней свободы» распределения. Величина  равна

, (2.6)

где s – число независимых условий (связей), наложенных на частоты p^*_i. Примерами таких связей могут быть:

1) {это должно быть всегда};

2) {среднее арифметическое должно совпадать с математическим ожиданием};

3) {должны совпадать теоретическая и выборочная дисперсии}.

Могут быть другие связи.

Для распределения ² составлены специальные таблицы. Пользуясь ими, можно для каждого значения ² и числа степеней свободы  найти вероятность p того, что величина, распределенная по закону ², превзойдет это значение.

Распределение ² дает возможность оценить степень согласованности теоретического и статистического распределений. Будем исходить из того, что случайная величина X действительно распределена по закону F(x). Тогда вероятность p, определенная по таблице, есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического распределений будет не меньше, чем полученное значение ². Если эта вероятность мала, то результат опыта следует считать противоречащим гипотезе о том, что закон распределения случайной величины

---

Х есть F(x).

Соответствие теоретического и статистического распределений проводится в следующей последовательности:

1) Определяется мера расхождения

.

2) Определяется число степеней свободы

.

3) По  и ² по таблице определяется вероятность того, что величина, имеющая распределение ² с  степенями свободы, будет иметь отклонение, большее, чем наблюдаемое в опыте ² .

Насколько мала должна быть вероятность р для того, чтобы отвергнуть гипотезу о совпадении распределений, является предметом соглашения. Обычно принимают, что при p < 0,1 наблюдаемое расхождение является принципиальным, поэтому следует попытаться подобрать другой закон распределения.

Следует отметить, что с помощью критерия ² можно только лишь опровергнуть гипотезу, что распределения совпадают. Если вероятность р велика, то этот факт свидетельствует только о том, что наблюдаемое статистическое распределение не противоречит теоретическому распределению. Однако при этом может быть другое распределение, которое также не противоречит наблюдаемым данным.

Если вероятность р, определенная по таблице, очень велика, то здесь следует обратить внимание на другую сторону проблемы. Если получили табличную вероятность р = 0,99, то это будет означать, что с вероятностью 0,99 расхождения должны быть больше, чем наблюдаемые в опытах. Тогда можно предположить, что расхождение является не случайным, а вызвано другими причинами, например подчисткой данных, когда не все результаты вносятся в протокол измерений. По такой схеме проверяются результаты выборов, опросов и т.д.

---

Задание на лабораторную работу
По данным лабораторной работы №1 проверить, соответствует ли распределение случайной величины х закону Гаусса.
Пример выполнения лабораторной работы
Выделим для выполнения работы Лист2 электронной таблицы EXCEL и на этом листе в ячейку А1 введем заголовок Лабораторная работа №2. Далее с листа1 скопируем статистический ряд, причем данные из столбцов перенесем в строки. На Листе1 выделим ячейки J3:J13, скопируем их в буфер обмена, активизируем на Листе2 ячейку А3, в меню Правка выберем команду Специальная вставка, установим опции транспонировать и значения и введем данные в ячейки А3:К3. В ячейки А4 и А5 запишем заголовки строк xminи xmax. Скопируем на Листе1 ячейки К4:К13 и аналогичным образом введем значения в строку В4:К4 листа2. Затем скопируем ячейки К5:К14 и вставим их значения в строку В5:К5. Далее скопируем ячейки М4:N13, активизируем ячейку В6 листа2 и с помощью команды Специальная вставка введем данные в ячейки В6:К7.

Для последующих вычислений потребуются значения среднеарифметического, дисперсии и среднеквадратичного отклонения случайной величины. При проведении вычислений на Листе2 в формулах можно ссылаться на ячейки, находящиеся на Листе1. Однако для удобства вычислений и большей наглядности перенесем эти характеристики на Лист2, в ячейках M3:M5 разместим заголовки величин, а в ячейках N3:N5 – их значения.

Далее найдем вероятности попадания случайной величины, распределенной по закону Гаусса, в каждый из интервалов. В ячейки А8 и А9 запишем заголовки строк значений функции распределения Ф и вероятности р. Для расчета значений функции распределения Гаусса воспользуемся встроенной функцией EXCELНОРМРАСП. Активизируем ячейку В8 и с помощью Мастера функций из раздела статистические вызовем эту функцию. На экране появится меню функции, показанное на рис.2.1.



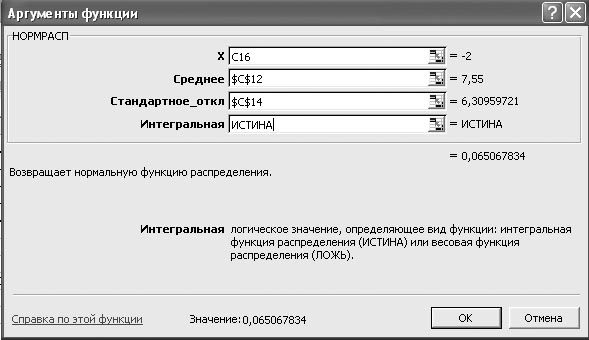
Рис. 2.1. Меню функции НОРМРАСП
Для всех интервалов за исключением первого функция распределения соответствует вероятности того, что случайная величина примет значение меньше верхней границы интервала. Поэтому в первой строчке меню укажем адрес верхней границы первого интервала В5. Во вторую ячейку введем адрес среднего арифметического N$3$,

---