Файл: Тема устойчивость сау. Алгебраические и частотные критерии устойчивости практика 5 (4 часа). Анализ устойчивости сау с помощью алгебраических и частотных критериев Пример 16.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 30.10.2023

Просмотров: 23

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Тема 6. УСТОЙЧИВОСТЬ САУ. АЛГЕБРАИЧЕСКИЕ И ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Практика 5 (4 часа).

Анализ устойчивости САУ с помощью

алгебраических и частотных критериев
Пример 16. На основании критерия Рауса-Гурвица получить условия устойчивости системы стабилизации частоты синхронного генератора. Определить критический коэффициент передачи системы 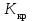из условия нахождения системы на колебательной границе устойчивости и провести её моделирование.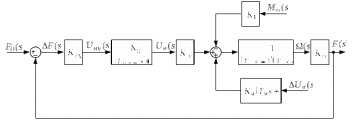



Рис. 31. ССДМ системы стабилизации частоты синхронного генератора
(Для примера расчета приняты следующие значения исходных данных:

Kиу = 5 В/Гц; Ku = 4,22; Ту.с.п. = 0,0125 с; Kдв = 1,706 рад/Вс; Тм = 0,4 с; Тв = 0,02 с;Kсг = 0,48 Гцс/рад; K1 = 10 1/Нмс; Kя = 227 рад/Вс; Мн = 0,2 Нм; f0 = 500 Гц; Uя = 2 В.)
Решение

Передаточная функция разомкнутой ССЧСГ



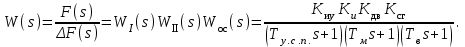
Характеристическое уравнение ССЧСГ



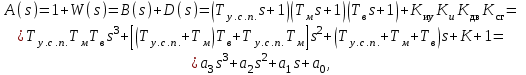
где

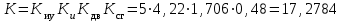
Определитель Гурвица для ССЧСГ

.

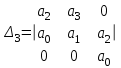Необходимое условие устойчивости:

, .

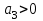
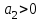
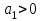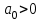Достаточное условие устойчивости: 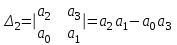 0.



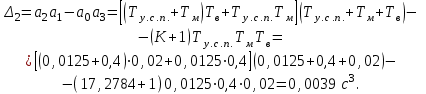
Так как полученное число является положительным, то достаточное условие устойчивости выполняется и ССЧСГ в целом является устойчивой.

Значение критического коэффициента передачи ССЧСГ определится из условия

=

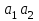
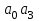
или

.

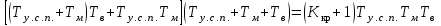Тогда

.

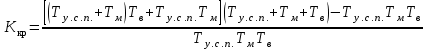Подставив в полученное выражение необходимые значения постоянных времени, найдём критический коэффициент передачи ССЧСГ



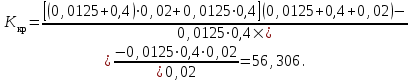
Проведём моделирование ССЧСГ с критическим значением коэффициента передачи ( 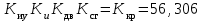) в системе MATLAB Simulink согласно ССДМ, представленной на рис. 45. Результаты моделирования представлены на рис. 47.



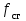, Гц

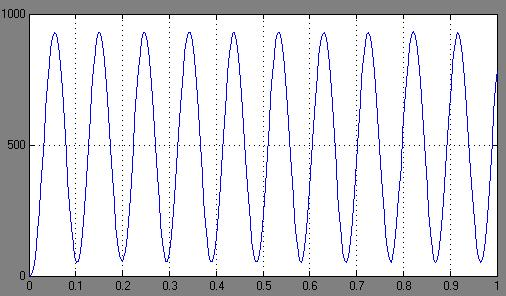t, c
Рис. 47. Переходная характеристика системы стабилизации частоты

синхронного генератора при критическом значении коэффициента передачи
Из графика видно, что переходный процесс в системе характеризуется незатухающими колебаниями, то есть она находится на колебательной границе устойчивости.
Расчетные задания для самостоятельной работы

Исходные данные по вариантам (см. таблица 7) согласно ССДМ ССЧСГ (см. рис. 31).
Контрольные вопросы

1. Поясните, что означает критический коэффициент передачи САУ

2. Расскажите, что является необходимым условием устойчивости САУ 3. Запишите достаточное условие устойчивости САУ

Таблица 7

П араметры
Вариант
Kиу,

В/Гц
Ku
Ту.с.п.,

с
Kдв,

рад/Вс
Тм,

с
Тв,

с
Kсг,

Гцс/рад
K1,

1/Нмс
Kя,

рад/Вс
Мн,

Нм
f0,

Гц
Uя,

В

1
3
3,11
0,0105
1,205
0,2
0,01
0,41
5
200
0,1
300
1

2
4
4,22
0,0115
1,304
0,3
0,02
0,42
6
210
0,2
400
2

3
5
5,33
0,0120
1,408
0,4
0,03
0,43
7
220
0,3
500
3

4
6
3,11
0,0105
1,205
0,2
0,01
0,44
8
230
0,4
600
4

5
7
4,22
0,0115
1,304
0,3
0,02
0,45
9
200
0,2
300
1

6
3
5,33
0,0120
1,408
0,4
0,03
0,46
10
210
0,1
400
2

7
4
3,11
0,0105
1,205
0,2
0,01
0,47
11
220
0,2
500
3

8
5
4,22
0,0115
1,304
0,3
0,02
0,49
12
230
0,3
600
4

9
6
5,33
0,0120
1,408
0,4
0,03
0,41
13
200
0,4
300
1

10
7
3,11
0,0105
1,205
0,2
0,01
0,42
14
210
0,2
400
2

11
3
4,22
0,0115
1,304
0,3
0,02
0,43
15
220
0,1
500
3

12
4
5,33
0,0120
1,408
0,4
0,03
0,44
14
230
0,2
600
4

13
5
3,11
0,0105
1,205
0,2
0,01
0,45
13
200
0,3
300
1

14
6
4,22
0,0115
1,304
0,3
0,02
0,46
12
210
0,4
400
2

15
7
5,33
0,0120
1,408
0,4
0,03
0,47
11
220
0,2
500
3

16
3
3,11
0,0105
1,205
0,2
0,01
0,49
10
230
0,1
600
4

17
4
4,22
0,0115
1,304
0,3
0,02
0,41
9
200
0,2
300
1

18
5
5,33
0,0120
1,408
0,4
0,03
0,42
8
210
0,3
400
2

19
6
3,11
0,0105
1,205
0,2
0,01
0,43
7
220
0,4
500
3

20
7
4,22
0,0115
1,304
0,3
0,02
0,44
6
230
0,2
600
4

21
3
5,33
0,0120
1,408
0,4
0,03
0,45
5
200
0,1
300
1

22
4
3,11
0,0105
1,205
0,2
0,01
0,46
4
210
0,2
400
2

23
5
4,22
0,0115
1,304
0,3
0,02
0,47
3
220
0,3
500
3

24
6
5,33
0,0120
1,408
0,4
0,03
0,49
2
230
0,4
600
4

25
5
4,22
0,0125
1,706
0,4
0,02
0,48
10
227
0,2
500
2

26
4
5,33
0,0130
1.805
0,3
0,03
0,45
6
210
0,3
400
3

27
3
3,11
0,0135
1,304
0,2
0,47
0,44
4
220
0,1
300
1

Пример 17. На основании критерия устойчивости Найквиста оценить устойчивость ССЧСГ с помощью АФЧХ.

Решение

Определяем передаточную функцию разомкнутой системы



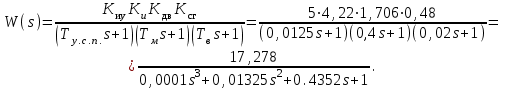
Для построения АФЧХ запишем следующую программу:

%исходные данные

R = 1; %радиус

% координаты начала

x0 = 0;

y0 = 0;

 % задаем окружность в параметрическом виде

 t = 0:0.001:2*pi;

x = x0 + R.*cos(t);

y = y0 + R.*sin(t);

 % строим график

 plot(x,y,'r:')

hold on

 

num=[17.278];

den=[0.0001 0.01325 0.4352 1];

sys=tf(num, den);

nyquist(sys)
Результаты моделирования представлены на рис. 48.

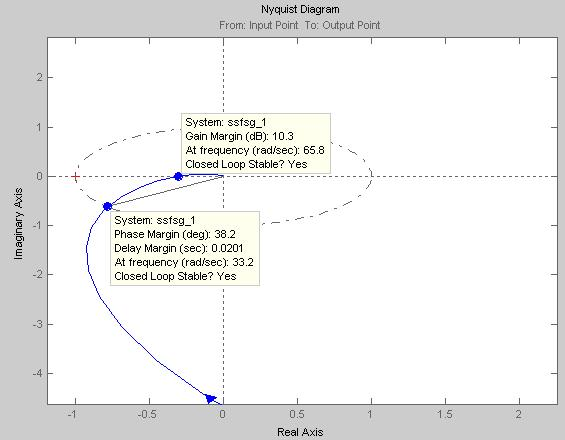
Рис. 48. АФЧХ ССЧСГ
На графике штрихпунктирной линией показана окружность единичного радиуса. При изменении частоты от нуля до бесконечности АФЧХ вначале пересекает окружность, а затем отрицательную вещественную полуось, следовательно, АФЧХ не охватывает точку с координатами – 1; j0 и система является устойчивой.
Расчетные задания для самостоятельной работы

Исходные данные по вариантам (см. таблица 7) согласно ССДМ ССЧСГ (см. рис. 31).
Контрольные вопросы

1. Назовите необходимые и достаточные условия для определения устойчивости замкнутой линейной стационарной минимально-фазовой системы по АФХ

2. Поясните, как определить запас устойчивости по фазе по АФЧХ

3. Поясните, как определить запас устойчивости по амплитуде по АФЧХ

Пример 18. На основании критерия Найквиста оценить устойчивость САУ по АФЧХ и ЛЧХ, если передаточная функция разомкнутой системы имеет вид

.
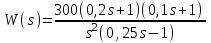Решение

Система имеет два интегрирующих звена, то есть 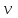= 2 и при ω = 0 аргумент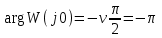
. Характеристический многочлен системы имеет два нулевых корня 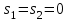и один вещественный положительный корень 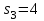, следовательно, l = 1.

Для построения АФЧХ преобразуем передаточную функцию

.

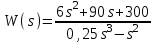Составляем программу для построения АФЧХ:
num=[6 90 300];

den=[0.25 -1 0 0];

sys=tf(num,den);

nyquist(sys)
Результаты моделирования представлены на рис. 49.

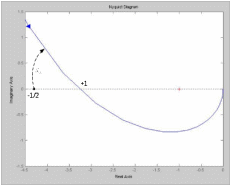
Рис. 49. АФЧХ исследуемой системы
Поскольку l = 1, то АФЧХ необходимо дополнить дугой бесконечно большого радиуса по часовой стрелке от вещественной отрицательной полуоси, как показано на рис. 49. В результате имеем отрицательный полупереход 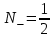и один положительный переход 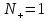. Разность между числом положительных и отрицательных переходов 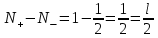, то есть замкнутая САУ будет устойчивой.

Для построения ЛЧХ необходимо записать следующую программу:
num=[6 90 300];

den=[0.25 -1 0 0];

sys=tf(num,den);

bode(sys)
На рис. 50 представлены ЛЧХ исследуемой системы.

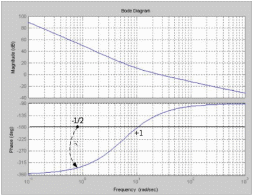
Рис. 50. ЛЧХ исследуемой системы
Из сравнительного анализа полученных графиков с графиком АФЧХ (см. рис. 49) следует, что дуга бесконечно большого радиуса будет начинаться на линии –180° и даст отрицательный полупереход 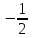. Положительный переход определяется при пересечении ЛФЧХ линии –180° снизу вверх до частоты среза ωс (частоты, при которой ЛАЧХ переходит через линию 0 дБ).
Расчетные задания для самостоятельной работы

















































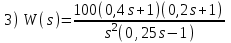
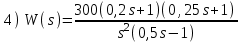
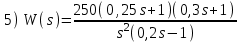
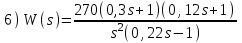
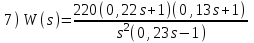
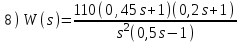
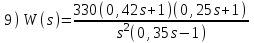
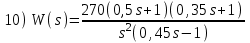
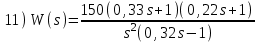
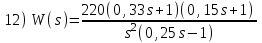
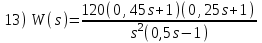
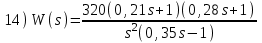
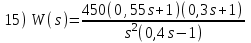
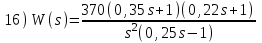
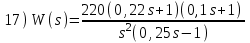
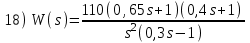
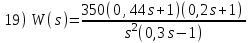
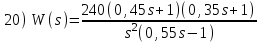
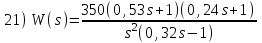
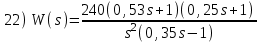
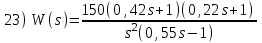
Контрольные вопросы

1. Поясните особенности анализа устойчивости астатических систем.

2. Сформулируйте правило переходов.

Смотрите также файлы