Файл: Задача 1 14 1,1 6,9 19 1,1 19 4890 19 34,1 19 390 19 1,4 19 4020 19 27,7 19 1489 19 1,6 19 11960 19.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 47

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Значения параметров a и b линейной модели определим, используя данные расчетной таблицы.
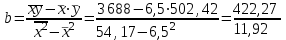= 35,4.

= 502,42 – 35,46,5 = 272,32.
Уравнение регрессии имеет вид: .

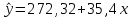Рассчитаем на основе полученного уравнения регрессии теоретические значения товарной продукции.


Условный год, x
Добыча газа, y
Теоретические значения y

1
287
307,72

2
325
343,12

3
364
378,52

4
413
413,92

5
462
449,32

6
503
484,72

7
544
520,12

8
590
555,52

9
616
590,92

10
641
626,32

11
643
661,72

12
641
697,12


Нанесем эти значения на график.

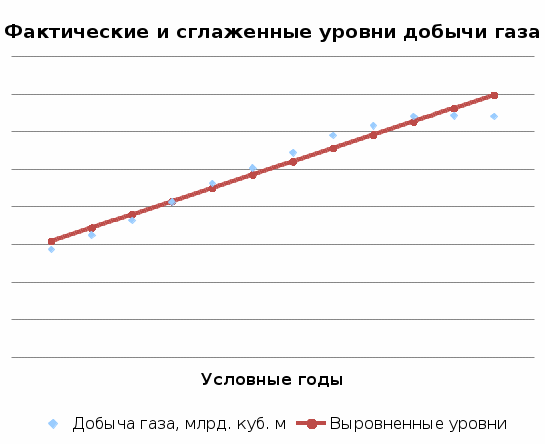
Анализ полученных результатов показывает, что в рассмотренный период наблюдалось увеличение добычи газа, хотя к концу рассматриваемого периода темп роста значительно снизился.
Задача 10
По данным Вашего варианта выполнить следующее:

а) исчислить индивидуальные цепные индексы цен;

б) исчислить сводные цепные индексы цен;

в) исчислить сводные цепные индексы товарооборота и физического объема проданных товаров;

г) исчислить сводный индекс цен в среднегармонической форме;

д) проверить правильность расчетов, используя взаимосвязи индексов
;

е) исчислить сводные базисные и цепные индексы цен с постоянными и переменными весами.

Решение: Рассчитаем цены за каждый период, разделив стоимость оборота на количество проданных товаров, выразив результат в рублях.

Например, найдем цену лука в январе:

302  1000 : 754,6 = 400,2 руб.

Полученные значения поместим в таблицу.


Наименование товара
Январь
Февраль
Март
Апрель
Май

Количество проданных товаров, ц
Цена, руб.
Количество проданных товаров, ц
Цена, руб.
Количество проданных товаров, ц
Цена, руб.
Количество проданных товаров, ц
Цена, руб.
Количество проданных товаров, ц
Цена, руб.

Лук
754,6
400,2
827,1
599,7
578,4
700,2
654,3
690,8
458,3
650,2

Свекла
319,9
250,1
355,9
283,8
274,9
301,9
364,1
348,8
255,7
348,1

Морковь
221,9
667,0
294,5
848,9
226,2
981,4
288,6
1001,4
227,1
999,6

Вычислим индивидуальные индексы цен в феврале по сравнению с январем:

Лук: ip = 599,7 : 400,2 = 1,499;

Свекла: ip = 283,8 : 250,1 = 1,135;

Морковь: ip = 848,9 : 667,0 = 1,273.

Определим сводный индекс цен.

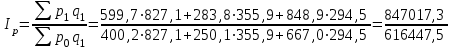= 1,374 = 137,4%.

Определим сводный индекс товарооборота.

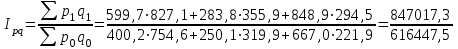= 1,598 = 159,8%.

Определим сводный индекс физического объема проданных товаров.

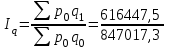= 1,163 = 116,3%.

Вычислим сводный индекс цен в среднегармонической форме.

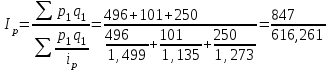
= 1,374 = 137,4%.

Проверим правильность расчетов, используя взаимосвязи индексов.

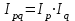= 1,374  1,163 = 1,598.

Вычислим индивидуальные индексы цен в марте по сравнению с февралем:

Лук: ip = 700,2 : 599,7 = 1,168;

Свекла: ip = 301,9 : 283,8 = 1,064;

Морковь: ip = 981,4 : 848,9 = 1,156.

Определим сводный индекс цен.

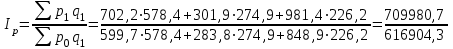= 1,151 = 115,1%.

Определим сводный индекс товарооборота.

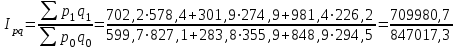= 0,838 = 83,8%.

Определим сводный индекс физического объема проданных товаров.

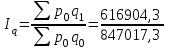= 0,728 = 72,8%.

Вычислим сводный индекс цен в среднегармонической форме.

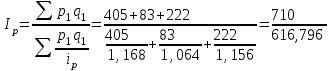= 1,151 = 115,1%.

Проверим правильность расчетов, используя взаимосвязи индексов.

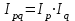= 1,151  0,728 = 0,838.

Вычислим индивидуальные индексы цен в апреле по сравнению с мартом:

Лук: ip = 690,8 : 700,2 = 0,987;

Свекла: ip = 348,8 : 301,9 = 1,155;

Морковь: ip = 1001,4 : 981,4 = 1,02.

Определим сводный индекс цен.

=

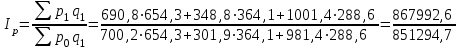= 1,02 = 102%.

Определим сводный индекс товарооборота.

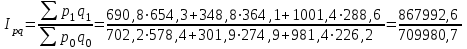=1,223=122,3%.

Определим сводный индекс физического объема проданных товаров.

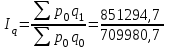= 1,199 = 119,9%.

Вычислим сводный индекс цен в среднегармонической форме.

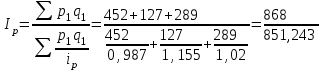= 1,02 = 102%.

Проверим правильность расчетов, используя взаимосвязи индексов.

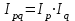= 1,02  1,199 = 1,223.

Вычислим индивидуальные индексы цен в мае по сравнению с апрелем:

Лук: ip = 650,2 : 690,8 = 0,941;

Свекла: ip = 348,1 : 348,8 = 0,998;

Морковь: ip = 999,6 : 1001,4 = 0,998.

Определим сводный индекс цен.

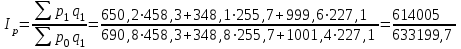= 0,97 = 97%.

Определим сводный индекс товарооборота.

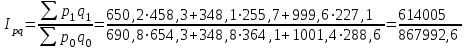=0,707= 70,7%.

Определим сводный индекс физического объема проданных товаров.

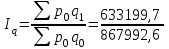
= 0,729 = 72,9%.

Вычислим сводный индекс цен в среднегармонической форме.

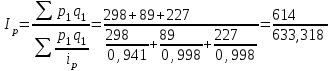= 0,969 = 96,9%.

Проверим правильность расчетов, используя взаимосвязи индексов.

= 0,97  0,729 = 0,707.

Вычислим сводные базисные индексы цен с постоянными весами.

Определим сводный индекс цен за февраль.

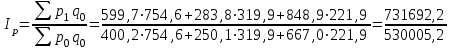= 1,38 = 138%.

Определим сводный индекс цен за март.

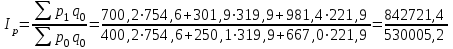= 1,59 = 159%.

Определим сводный индекс цен за апрель.

=

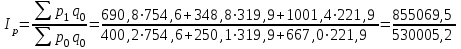= 1,613 = 161,3%.

Определим сводный индекс цен за май.

=

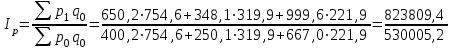= 1,554 = 155,4%.

Вычислим сводные базисные индексы цен с переменными весами.

Определим сводный индекс цен за февраль.

= 1,374 = 137,4%.

Определим сводный индекс цен за март.

=

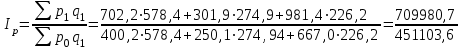= 1,574 = 157,4%.

Определим сводный индекс цен за апрель.

=

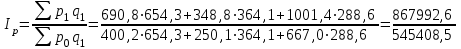= 1,591 = 159,1%.

Определим сводный индекс цен за май.

=

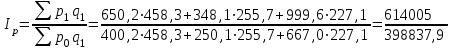= 1,539 = 153,9%.

Задача 11
На основе выборочного метода из 30 предприятий Вашего варианта произвести отбор 10 предприятий, укажите способ отбора и рассчитайте по отобранным предприятиям:

1) среднюю стоимость промышленно-производственных основных фондов;

2) предельную ошибку этой средней и пределы, в которых можно полагать генеральную среднюю с вероятностью 0,954;

3) генеральную среднюю;

4) сравните результаты расчетов, полученных в пункте 1,2,3 и сформулируйте выводы.

Решение: Произведем отбор 10 предприятий и вычислим среднюю стоимость промышленно-производственных основных фондов, дисперсию и среднее квадратичное отклонение.

Составим вспомогательную таблицу.

№ п/п
Стоимость ОПФ, xi
(x – )2

1
1,1
4,5369

2
1,4
3,3489

3
1,6
2,6569

4
2,8
0,1849

5
3,3
0,0049

6
4,1
0,7569

7
4,2
0,9409

8
4,5
1,6129

9
4,6
1,8769

10
4,7
2,1609

Итого
32,3
18,081

Получим: = 32,3 : 10 = 3,23 млн. р.

Dв =18,081 : 10  1,8.

Вычислим среднее квадратичное отклонение:

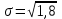= 1,34.

Определим с вероятностью 0,954 предельную ошибку средней.

Используем для этого формулу: 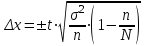, где σ – среднее квадратичное отклонение, n – объем выборки, 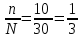. Значение t найдем по таблице значений функции Лапласа. Для вероятности 0,954 значение t составляет 2.

Получаем: 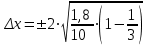= 0,69.

Запишем пределы для генеральной средней.



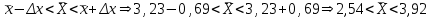
Точечной оценкой генеральной средней является выборочная средняя, т.е.

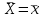= 3,23 млн. р.

Таким образом, с вероятностью 0,954 можно утверждать, что средняя стоимость промышленно-производственных основных фондов в генеральной совокупности находится в пределах от 2,54 млн. р. до 3,92 млн. р.




Список использованной литературы

  1. Теория статистики /Под ред. Р.А.Шмойловой.-М., Финансы и статистика, 2000.

  2. Долгова В.Н. Статистика: учебник и практикум / В.Н. Долгова, Т.Ю. Медведева. – М.: Юрайт, 2017.

  3. Елисеева И.И., Юзбашев М.М. Общая теория статистики. - М., Финансы и статистика, 2000.

  4. Ефимова М.Р. Практикум по общей теории статистики: учеб. пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова. – М.: Финансы и статистика, 2011.

  5. Общая теория статистики /Под ред. А.А.Спирина и О.Э.Башиной. - М., Финансы и статистика, 2000.

  6. Гусынин А.Б., Минашкин В.Г., Садовникова Н.А., Шмойлова Р.А. Теория статистики: Учебно-практ. Пособие для системы дистанционного образования М.: МЭСИ, 2000

  7. Минашкин В.Г. Статистика: учебник для бакалавров / В.Г. Ми- нашкин. – М.: Юрайт, 2016.

  8. Практикум по теории статистики /Под ред. Р.А.Шмойловой - М., Финансы и статистика,2000.

  9. Султанова С.М. Статистика. Учебник. – Ташкент, 2021 г.

Смотрите также файлы