Файл: Задача 1 14 1,1 6,9 19 1,1 19 4890 19 34,1 19 390 19 1,4 19 4020 19 27,7 19 1489 19 1,6 19 11960 19.docx
Добавлен: 06.11.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Получим:
= 20433 : 30 = 681,1 чел.Dв =3091783 : 30 = 103059,4.
Вычислим среднее квадратичное отклонение:
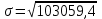= 321 чел.Вычислим коэффициент вариации.
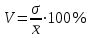= 321 : 681,1 100 = 47,1%.Определим моду. Модальный интервал - это интервал с наибольшей частотой. В нашем случае это интервал (291; 540). Значение моды определим по формуле:
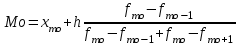
где
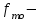частота в модальном интервале, 
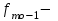частота в интервале, предшествующем модальному, 
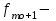частота в интервале, следующим за модальным, 
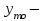нижняя граница модального интервала, h - величина модального интервала. В нашем случае: 
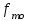= 13, 
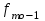= 0,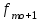 
= 10, h = 249.Получим:
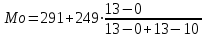= 493,3 чел.Определим медиану. Медианный интервал - это интервал, в котором значение накопленной частоты достигает значения, равного половине суммы частот, т.е.
30 : 2 = 15. Вычислим накопленные частоты.
S1 = 13; S2 = 13 + 10 = 23.
Таким образом, медианный интервал: (540 ; 789). Значение медианы определим по формуле:
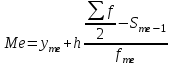
где
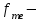частота медианного интервала, 
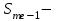накопленная частота в интервале, предшествующем медианному, 
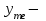нижняя граница медианного интервала, h - величина медианного интервала. В нашем случае:
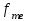
= 10,
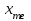= 540, 
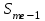= 13.Получим:
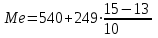= 589,8 чел.| Интервалы | Частоты, ni | Относительные частоты | Накопленные частоты | Середина интервала, xi | xini | (x – )2ni |
| 291 - 540 | 13 | 0,43 | 13 | 415,5 | 5401,5 | 917063,7 |
| 540 - 789 | 10 | 0,33 | 23 | 664,5 | 6645 | 2755,6 |
| 789 - 1038 | 2 | 0,07 | 25 | 913,5 | 1827 | 108019,5 |
| 1038 - 1287 | 2 | 0,07 | 27 | 1162,5 | 2325 | 463491,9 |
| 1287 - 1536 | 3 | 0,10 | 30 | 1411,5 | 4234,5 | 1600452 |
| | 30 | | | | 20433 | 3091783 |
Для расчета квартилей воспользуемся формулами:
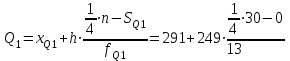= 434,7 чел.
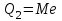= 589,8 чел.
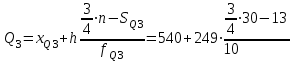= 776,6 чел.
Задача 7
По данным любого статистического ежегодника органов госстатистики или по данным периодических изданий построить диаграммы: столбиковую, круговую, секторную, фигур-знаков, знак варзара, линейную, радиальную и картограмму.
Решение: Используем следующие статистические данные (Российский статистический сборник 2006).
14.27. ВАЛОВОЙ СБОР ЗЕРНА ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ (в хозяйствах всех категорий; тысяч тонн)
| | В среднем за год | 2001 | 2002 | 2003 | 2004 | 2005 | |||||||||
| 1976- 1980 | 1981 - 1985 | 1986- 1990 | 1991- 1995 | 1996- 2000 | | | | | | ||||||
| Центральный федеральный округ | | | | | 120367 | 13964 | 15720 | 12653 | 13438 | 14709 | |||||
| Белгородская область | 1758 | 1408 | 2099 | 1697 | 1237 | 1733 | 1950 | 1310 | 1698 | 2031 | |||||
| Брянская область | 833,5 | 735,6 | 1019 | 911,0 | 453,3 | 452,7 | 518,2 | 393,3 | 492,3 | 492,3 | |||||
| Владимирская область | 481,3 | 441,1 | 489,6 | 368,6 | 223,1 | 236,6 | 248,0 | 180,1 | 171,5 | 172,4 | |||||
| Воронежская область | 3146 | 2305 | 3638 | 2727 | 1906 | 2463 | 2582 | 2283 | 2356 | 2414 | |||||
| Ивановская область | 378,5 | 335,0 | 390,1 | 328,5 | 180,7 | 165,4 | 115,9 | 99,6 | 102,7 | 92,9 | |||||
| Калужская область | 472,1 | 435,7 | 540,0 | 439,6 | 201,1 | 148,1 | 166,1 | 136,9 | 145,0 | 121,0 | |||||
| Костромская область | 298,8 | 292,7 | 278,3 | 239,6 | 154,6 | 143,4 | 95,8 | 82,7 | 69,9 | 73,8 | |||||
| Курская область | 1962 | 1728 | 2445 | 2047 | 1363 | 1573 | 1957 | 1346 | 1599 | 1900 | |||||
| Липецкая область | 1355 | 1159 | 1827 | 1638 | 1093 | 1403 | 1621 | 1497 | 1498 | 1908 | |||||
| Московская область | 772,8 | 677,0 | 734,5 | 502,5 | 326,0 | 305,0 | 349,7 | 252,2 | 285,2 | 210,4 | |||||
| Орловская область | 1225 | 1155 | 1794 | 1744 | 1192 | 1614 | 1967 | 1512 | 1577 | 1664 | |||||
| Рязанская область | 1351 | 1161 | 1641 | 1359 | 847,3 | 823,9 | 946,9 | 751,9 | 811,7 | 873,9 | |||||
| Смоленская область | 707,8 | 724,9 | 712,1 | 599,8 | 286,5 | 195,0 | 198,6 | 162,4 | 195,1 | 148,6 | |||||
| Тамбовская область | 2063 | 1682 | 2196 | 1804 | 1271 | 1521 | 1704 | 1568 | 1315 | 1581 | |||||
| Тверская область | 656,9 | 733,5 | 704,8 | 475,4 | 267,6 | 206,4 | 180,2 | 160,2 | 169,7 | 128,7 | |||||
| Тульская область | 1210 | 1300 | 1596 | 1478 | 873,0 | 809,3 | 1006 | 816,8 | 861,6 | 827,7 | |||||
| Ярославская область | 346,2 | 344,2 | 301,0 | 225,2 | 162,2 | 172,1 | 113,8 | 101,0 | 90,5 | 69,7 | |||||
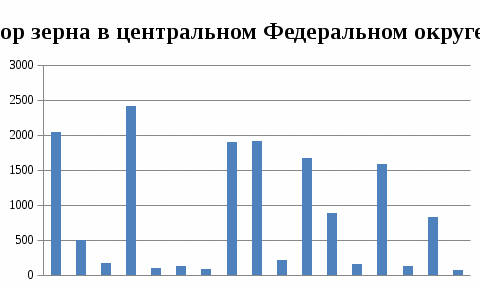
Построим по данным о валовом сборе зерна за 2005 год столбиковую, круговую, секторную, фигурную, линейную и радиальную диаграмму.
Фигурные диаграммы (диаграммы фигур — знаков) отображают размер изучаемого объекта в соответствии с размером своей площади. Рисунки, фигуры отличаются друг от друга размером (соответственно величине показателя), либо величины статистических показателей изображаются на рисунках определенным количеством одинаковых по размеру и типу фигур.
Столбиковая диаграмма
Круговая диаграмма
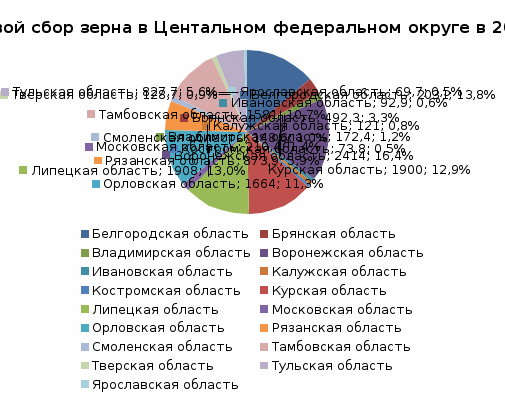
Секторная диаграмма
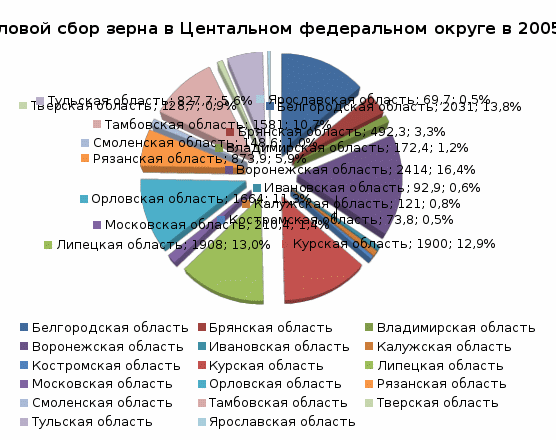
Линейная диаграмма
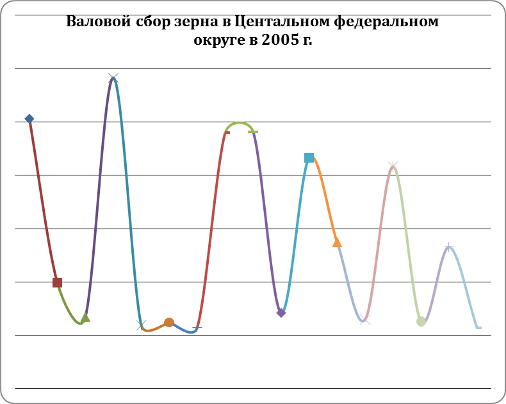
Радиальная диаграмма
Изобразим показатели посевной площади, урожайности и валового сбора с помощью знаков Варзара. Для этого построим прямоугольники, у которых ширина пропорциональна урожайности, а высота – посевной площади.
Изобразим с помощью картограммы среднюю месячную температуру воздуха в Российской Федерации в январе 2005 г.
| СРЕДНЯЯ МЕСЯЧНАЯ ТЕМПЕРАТУРА ВОЗДУХА В РОССИЙСКОЙ ФЕДЕРАЦИИ в январе 2005 г. |    Средняя месячная температура воздуха (0С) 2005 год  |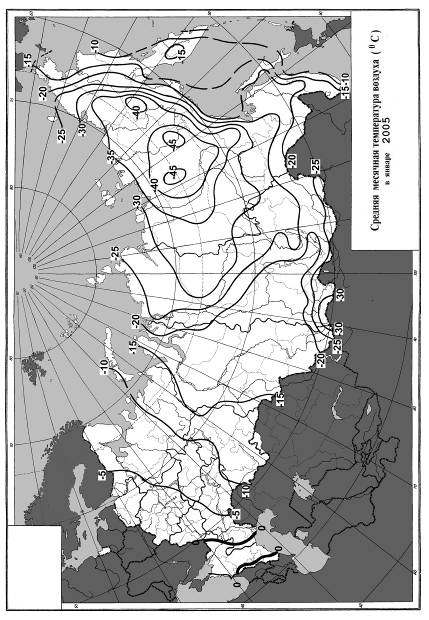
Задача 8
По данным о среднегодовой стоимости промышленно-производственных основных фондов и товарной продукции (возьмите 15 вариантов Вашего варианта из таблицы 1) выполните следующее:
1) построить по этим показателям ряд параллельных данных; определите наличие связи, изобразив графически парную связь между результативным и факторным признаками;
2) рассчитайте парный линейный коэффициенты корреляции связи между изучаемыми признаками, а также ранговый коэффициент корреляции;
3) выберите уравнение связи и вычислите параметры уравнения регрессии, рассчитайте на его основе теоретические значения товарной продукции и нанесите эти значения на построенный в пункте 1 график;
4) Дайте экономическую интерпретацию уравнения связи;
5) Все промежуточные расчеты изложите в табличной форме.
Решение: Для анализа выберем следующие показатели: x – стоимость основных производственных фондов – факторный признак и y – объем производства изделий – результативный признак.
Изобразим зависимость объема производства от среднегодовой стоимости ОПФ в виде точечной диаграммы.
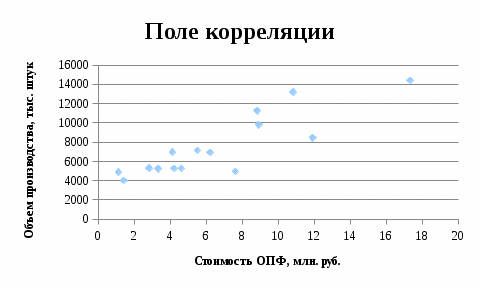
Точки на приведенном графике располагаются вблизи некоторой прямой, что позволяет предположить, что между указанными показателями существует линейная зависимость.
Измерим степень тесноты связи между факторным и результативным признаками.
Определим линейный коэффициент парной корреляции по следующей формуле:
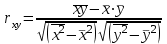
Составим вспомогательную таблицу.
| № предприятия | x | y | x2 | y2 | xy |
| 1 | 7,6 | 4970 | 57,76 | 24700900 | 37772 |
| 2 | 4,1 | 6960 | 16,81 | 48441600 | 28536 |
| 3 | 1,4 | 4020 | 1,96 | 16160400 | 5628 |
| 4 | 17,3 | 14410 | 299,29 | 207648100 | 249293 |
| 5 | 8,9 | 9780 | 79,21 | 95648400 | 87042 |
| 6 | 4,2 | 5250 | 17,64 | 27562500 | 22050 |
| 7 | 4,6 | 5260 | 21,16 | 27667600 | 24196 |
| 8 | 1,1 | 4890 | 1,21 | 23912100 | 5379 |
| 9 | 6,2 | 6915 | 38,44 | 47817225 | 42873 |
| 10 | 2,8 | 5290 | 7,84 | 27984100 | 14812 |
| 11 | 11,9 | 8450 | 141,61 | 71402500 | 100555 |
| 12 | 5,5 | 7145 | 30,25 | 51051025 | 39297,5 |
| 13 | 3,3 | 5215 | 10,89 | 27196225 | 17209,5 |
| 14 | 10,8 | 13170 | 116,64 | 173448900 | 142236 |
| 15 | 8,8 | 11250 | 77,44 | 126562500 | 99000 |
| Сумма | 98,5 | 112975,0 | 918,2 | 997204075,0 | 915879,0 |
| Среднее | 6,6 | 7531,7 | 61,2 | 66480271,7 | 61058,6 |