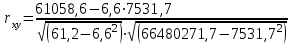= 0,8725.
По значению линейного коэффициента парной корреляции можно заключить, что между рассматриваемыми признаками существует тесная прямая корреляционная связь.

Вычислим выборочный коэффициент ранговой корреляции Спирмена.

Расположим значения x в порядке возрастания. Пронумеруем значения строки значений x от 1 до 15. Пронумеруем также значения строки y от 1 до 15, учитывая порядок их расположения.
Получим следующую таблицу:

Ранг	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
x	1,1	1,4	2,8	3,3	4,1	4,2	4,6	5,5	6,2	7,6	8,8	8,9	10,8	11,9	17,3
Ранг	2	1	7	4	9	5	6	10	8	3	13	12	14	11	15
y	4890	4020	5290	5215	6960	5250	5260	7145	6915	4970	11250	9780	13170	8450	14410

Вычислим значения d_i.

d₁ = 1 – 2 = -1; d₂ = 2 – 1 = 1; d₃ = 3 – 7 = -4;

d₄ = 4 – 4 = 0; d₅ = 5 – 9 = -4; d₆ = 6 – 5 = -1;

d₇ = 7 – 6 = 1; d₈ = 8 – 10 = -2; d₉ = 9 – 8 = 1;

d₁₀ = 10 – 3 = 7; d₁₁ = 11 – 13 = -3; d₁₂ = 11 – 12 = 0;

d₁₃ = 13 – 14 = -1; d₁₄ = 14 – 11 = 3; d₁₅ = 15 – 15 = 0.
Вычислим

---

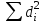
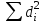
= (-1)² + 1² + (-4)² + 0² + (-4)² + (-1)² + 1² + (-2)² + 1² + 7²+ (-3)² + 0² + (-1)² + 3² + 0² = 104.
Выборочный коэффициент ранговой корреляции Спирмена найдем по формуле:
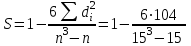= 0,8143.
Составим уравнение линейной регрессии в виде: .

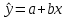Значения параметров a и b линейной модели определим, используя данные расчетной таблицы.
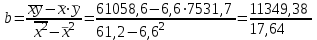= 643,4.

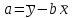= 7531,7 – 643,46,6 = 3285,3.
Уравнение регрессии имеет вид: .

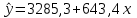Таким образом, с увеличением стоимости ОПФ на 1 млн. р. выпуск продукции в целом возрастает на 643,4 шт.

Рассчитаем на основе полученного уравнения регрессии теоретические значения товарной продукции.

Стоимость основных производственных фондов, млн. руб.	Объем производства изделий, тыс. шт.	Теоретические значения y
7,6	4970	8175,14
4,1	6960	5923,24
1,4	4020	4186,06
17,3	14410	14416,12
8,9	9780	9011,56
4,2	5250	5987,58
4,6	5260	6244,94
1,1	4890	3993,04
6,2	6915	7274,38
2,8	5290	5086,82
11,9	8450	10941,76
5,5	7145	6824,00
3,3	5215	5408,52
10,8	13170	10234,02
8,8	11250	8947,22

Нанесем эти значения на построенный в пункте 1 график.


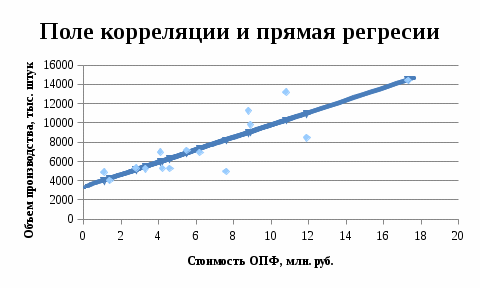
Полученное уравнение регрессии 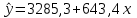показывает, что с увеличением стоимости ОПФ на 1 млн. р. выпуск продукции в целом возрастает на 643,4 шт.

---

Индивидуальная работа 3
Задача 9
По данным Вашего варианта выполнить следующее:

1. Изобразите графически динамику ряда с помощью статистической кривой.

2. Вычислите по данным этого ряда аналитические показатели: абсолютные, относительные средние; результаты расчетов изложите в табличной форме.

3. Произвести сглаживание ряда динамики с помощью скользящей средней и аналитического выравнивания. Полученные данные нанесите на график (см. пункт 1).

4. Сформулируйте выводы относительно основной тенденции развития ряда динамики.

Решение: Изобразите графически динамику ряда с помощью статистической кривой.

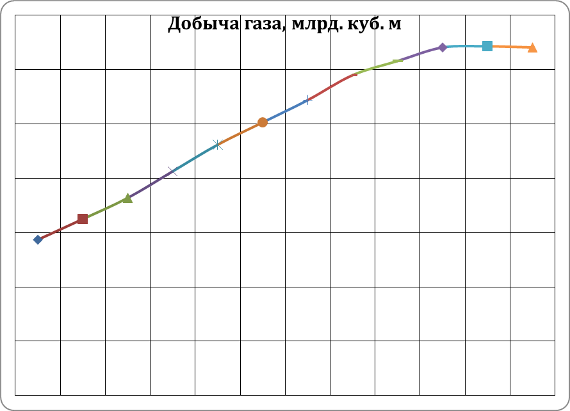
Абсолютные приросты вычислим по формуле A_t = x_t - x₀ (по базисной схеме) и a_t = x_t – x_t-1 (по цепной схеме). Темпы роста вычислим по формуле 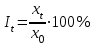(по базисной схеме) 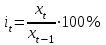(по цепной схеме). Темпы прироста вычислим по формуле 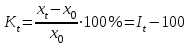(по базисной схеме), 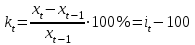(по цепной схеме).

Полученные значения поместим в таблицу

Годы	Добыча газа, млрд. куб. м	Абсолютные приросты, млрд. куб. м		Темпы роста, %		Темпы прироста, %
		Базисн.	Цепные	Базисн.	Цепные	Базисн.	Цепные
2010	287	-	-	-	-	-	-
2011	325	38	38	113,2	113,2	13,2	13,2
2012	364	77	39	126,8	112,0	26,8	12,0
2013	413	126	49	143,9	113,5	43,9	13,5
2014	462	175	49	161,0	111,9	61,0	11,9
2015	503	216	41	175,3	108,9	75,3	8,9
2016	544	257	41	189,5	108,2	89,5	8,2
2017	590	303	46	205,6	108,5	105,6	8,5
2018	616	329	26	214,6	104,4	114,6	4,4
2019	641	354	25	223,3	104,1	123,3	4,1
2021	643	356	2	224,0	100,3	124,0	0,3
2022	641	354	-2	223,3	99,7	123,3	-0,3
Сумма	6029

---

Вычислим среднегодовой уровень ряда динамики.
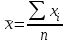= 6029 : 12 = 502,4 млрд. куб. м
Определим среднегодовые абсолютный прирост, темпы роста и прироста добычи газа.
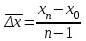= (641  287) : (12  1) = 32,2 млрд. куб. м.
Вычислим средние темпы роста и прироста
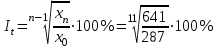= 1,0758 = 107,6%

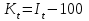= 107,6  100 = 7,6%
Произведем сглаживание ряда динамики трехзвенной скользящей средней.

Используем для этого формулы

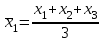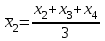, и т.д.

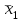= (287 + 325 + 364) : 3 = 325,3;

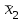= (325 + 364 + 413) : 3 = 367,3;

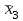= (364 + 413 + 462) : 3 = 413,0 и т.д.

Полученные данные представим в виде таблицы:

Годы	Добыча газа, млрд. куб. м	Выровненные уровни
2010	287	-
2011	325	325,3
2012	364	367,3
2013	413	413,0
2014	462	459,3
2015	503	503,0
2016	544	545,7
2017	590	583,3
2018	616	615,7
2019	641	633,3
2021	643	641,7
2022	641	-

---

Построим графическое изображение полученных рядов.


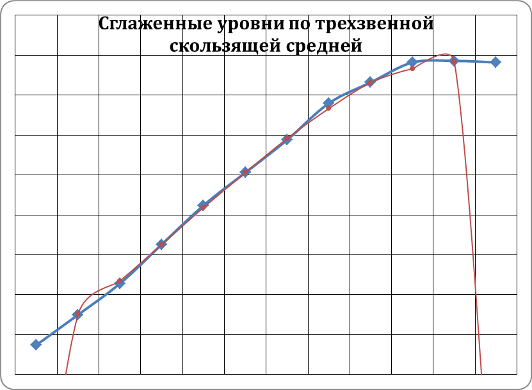
Произведем сглаживание ряда динамики с помощью аналитического выравнивания.
Составим вспомогательную таблицу.

№ п/п	Условный год, x	Добыча газа, y	x2	y2	xy
1	1	287	1	82369	287
2	2	325	4	105625	650
3	3	364	9	132496	1092
4	4	413	16	170569	1652
5	5	462	25	213444	2310
6	6	503	36	253009	3018
7	7	544	49	295936	3808
8	8	590	64	348100	4720
9	9	616	81	379456	5544
10	10	641	100	410881	6410
11	11	643	121	413449	7073
12	12	641	144	410881	7692
Сумма	78	6029	650	3216215	44256
Среднее	6,5	502,42	54,17	268017,92	3688,00

---

Смотрите также файлы

• Практическая работа 3 Маркировка углеродистых сталей и чугунов.docx

• 16. Опишите отряд приматы и этапы развития древних людей. 36. Охарактеризуйте особенности развития земной коры в докембрии.doc

• Образовательное учереждение.docx

• Общая характеристика работы 4 Глава.rtf

• 7. Опишите типы черви, членистоногие, мшанки. Их геологическое значение.doc