7. В чем сущность температурного режима при измерении размеров, как на него влияют величины измеряемых размеров?

Литература
1. ГОСТ 8.051-81. Государственная система обеспечения единства измерений. Погрешности, допускаемые при измерении линейных размеров до 500 мм.– Режим доступа: http://gostexpert.ru/gost/gost-8.051-81 (доступ свободный).

2. РД 50–98–86. Методические указания. Выбор универсальных средств измерения линейных размеров до 500 мм (по применению ГОСТ 8.051–81). – Режим доступа:http://www.gosthelp.ru/text/RD509886Metodicheskieukaz.html.

3. Санцевич, В. И. Допуски и технические измерения [Текст]: учебное пособие / В.И. Санцевич. – Мн.: ООО «Оракул», 1995.– 270 с.

4. ГОСТ 25347–82. Основные нормы взаимозаменяемости. Единая система допусков и посадок. Поля допусков и рекомендуемые посадки.– Режим доступа: http://gostexpert.ru/gost/gost-25347-82 (доступ свободный).
Практическая работа №2
Статистическая обработка результатов многократных измерений размера в партии деталей

Цель работы
Изучить и освоить методы статистической обработки результатов многократных измерений размеров
Комплектующие практической работы

1. 
   Партия контролируемых деталей.
   
2. 
   Чертеж детали.
   
3. 
   Микрометр с цифровым отсчетом и ценой деления 0,001 мм.
   
4. 
   Струбцина.
   
5. 
   Таблица статистических характеристик нормального распределения.
   

Методикаизмерений
Методика измерений сводится к проведению nнаблюдений (единичных измерений) и фиксированию nрезультатов многократных равноточных измерений одного и того же значения физической величины (линейного размера): Х₁, Х₂, … Х_n.

При этом принимается упрощение, заключающееся в том, что систематические погрешности результатов исключаются за счет настройки микрометра на номинальный размер по концевым мерам длины, измерений в узком диапазоне шкалы, закрепления микрометра в струбцине для исключения теплового воздействия рук экспериментатора, соблюдения постоянных условий измерений и т.п.

Таким образом, получается исправленная совокупность результатов измерений Х₁, Х₂, … Х_n.
Пояснение к условию проведения измерений
Задание является коллективным, т. е. одновариантным. Группа студентов выполняет измерение одного и того же диаметрального размера в партии деталей из 30 шт. Предполагается, что детали выполнены обработкой на одном станке одним рабочим. Измерение проводится одним студентом с использованием одного измерительного средства – микрометра с цифровой индикацией и ценой деления 0,001 мм, установленного в специальном приспособлении – струбцине, чтобы стабилизировать условия измерения и, прежде всего, избежать влияния температурного фактора нагрева микрометра от рук оператора. Такие измерения можно отнести к равноточным.

---

Схема измерения представлена на рисунке 1,эскиз детали – на рисунке 2.

Предполагается, что погрешности результатов измерений должны иметь нормальное распределение, это подтверждает практика контроля размеров деталей, обработанных резанием на металлорежущих станках. Данное предположение должно быть подтверждено формой гистограммы, построенной по результатам измерений.


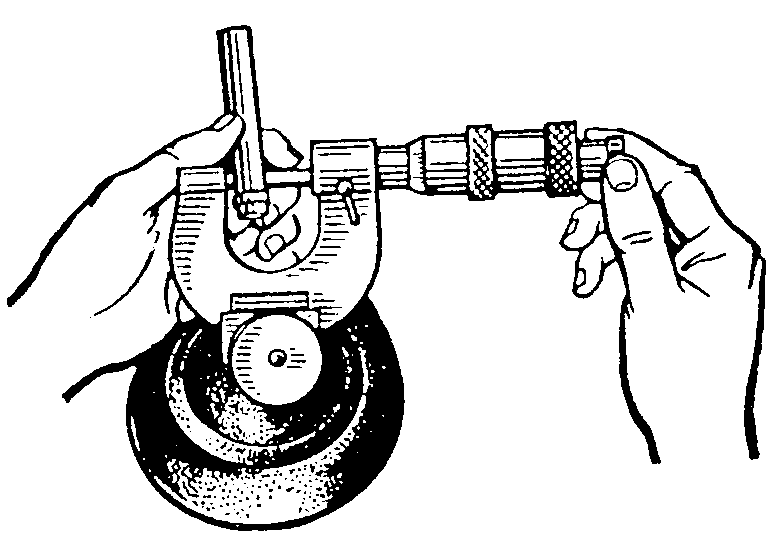
Рисунок 1 – Схема измерения



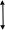
Рисунок 2 – Измеряемый размер детали

---

Построение гистограммы
Результаты многократных n измерений одной и той же величины можно представить диаграммой, которая показывает, как часто при измерениях получаются те или иные значения. Для этого весь диапазон измеренных значений, отложенных по оси Х, разбивают на равные интервалы, ширина которых ∆Х выбирается так, как это удобно. Затем подсчитывают число m значений измеряемой величины, попавших в каждый интервал, строят прямоугольники с основанием, равным выбранной ширине интервала и высотой, равной числу m значений измеренной величины в каждом интервале.

В результате в случае распределения погрешностей по нормальному закону получается диаграмма, изображенная на рисунке 3, называемая гистограммой. Для такого вида гистограммы целесообразно принимать нечетное число интервалов, чтобы получить островершинную диаграмму, и соответственно кривую.

Рисунок 3 – Типовая гистограмма нормального распределения результатов измерений

Если по оси ординат откладывать значения m/n, т. е. относительное число значений Х, попавших в интервал ∆Х, то вид гистограммы сохранится. В пределе, уменьшая величину ∆Х и увеличивая n, вместо гистограммы получают плавную кривую, называемую кривой распределения случайной величины, а функция, описывающая эту кривую – плотностью вероятности данного распределения или плотностью распределения данной величины.
Методика статистической обработки
Полученные результаты измерений обрабатываются в соответствии с положениями ГОСТ 8.207–76 [1] и материалами учебного пособия [2] в следующей последовательности:

1. 
   записывается исправленная совокупность результатов измерений: Х₁, Х₂, …, Х_n;
   
2. 
   определяется эмпирическое среднее математическое ожидание как среднее арифметическое исправленных результатов и принимается как оценка действительного значения размера
   

---

M[X] = X_дст ≈ X = 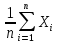(1)

3. 
   вычисляется оценка средней квадратической погрешности результата единичного измерения в ряду равноточных измерений в последовательности:
   

а) находится отклонение каждого результата от среднего арифметического Х₁–X, Х₂–X, …,Х_n–X;

б) проверяется правильность вычислений и, если они верны, то сумма отклонений равна нулю, т. е. Σ_i=1ⁿ (Х_i–X) = 0;

в) определяется оценка средней квадратической погрешности результата единичного измерения


σ[Х] ≈ S_x = 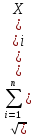/ (n – 1); (2)

4. 
   вычисляется оценка средней квадратической погрешности среднего арифметического (степень разброса величины Xотносительно М(Х))
   

S_x = 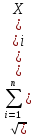/ n (n – 1) = S_x/n; (3)

5. 
   находятся границы доверительного интервала
   

Х – t·S_x<Х<Х+ t·S_x (4)
с двусторонней доверительной вероятностью Р_дов = 0,95 и Р_дов = 0,99, достаточной для большинства случаев технических измерений.

---

С учетом того, что количество измерений достаточно велико (n> 20), для определения значения безразмерного коэффициента t используется интеграл вероятности
Р( 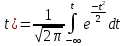. (5)
Интеграл табулирован и приводится в справочниках. В условиях настоящей лабораторной работы можно воспользоваться сокращенным вариантом таблицы интеграла вероятности в интервале его значений от 0,9 до 0,99 (таблица 1).
Таблица 1 – Выборка из таблицы интеграла вероятности(5)

t	1,65	1,70	1,75	1,81	1,88	1,96	2,05	2,20	2,35	2,60
Р(t)	0,901	0,911	0,920	0,930	0,940	0,950	0,960	0,972	0,981	0,991

Обнаружение и исключение грубых погрешностей
Для того, чтобы грубые погрешности измерения не искажали результат измерений, их следует исключить до того, как будет определяться оценка S_x и доверительный интервал ∆Х_р (или∆Х_р.n).

Разработан статистический критерий обнаружения грубых погрешностей для случая, когда группа обрабатываемых данных подчиняется нормальному закону распределения. В этом случае теория вероятностей позволяет при выбранной доверительной вероятности Р_дов рассчитать теоретически допустимые границы максимальных (по модулю) нормированных отклонений для выборки из n наблюдений[2]:
β_r ≈ max (X_i – X) / S_x (6)
Теоретически допустимые границы β_r табулированы для различных значений n при разных уровнях доверительной вероятности Р_дов (или разных уровнях значимости g, где g = 1 – Р_дов).

Применение статистического критерия обнаружения грубых погрешностей состоит в следующем. Вычислив

---

Смотрите также файлы

• 1Понятие продуктивной деятельности и особенности организации занятий по аппликации во второй младшей группе. 5.docx

• Европы христианские философы и богословы Фома Аквинский 1225 1274 xiiiв.docx

• Задание Норма права.docx

• Лабораторная работа 11 Исследование трехфазного синхронного генератора Цель работы.docx

• Задание Норма права.docx