Файл: Учебнометодическое пособие к практическим работам Волгодонск 2013 удк 006 621. 713 (076. 5) Ббк 34 М54.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 272
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
X и Sx, для некоторого результата Xk, имеющий наибольшее по модулю отклонение, определяют относительную величину нормированного отклонения
β*r =(Xk – X) / Sx. (7)
Задав уровень доверительной вероятностиРдов находят табличное значениеβr для числа n, соответствующего обрабатываемой выборке. Если β*r>βr, то результат Xk можно отбросить, в противном случае результат должен быть оставлен.
После исключения результата, содержащего грубую погрешность, значения X и Sx уточняются, так как число результатов в выборке уменьшилось. Затем выполняется описанная выше процедура для результата выборки, имеющего наибольшее по модулю отклонение от уточненного значения X.
Описанный порядок действия повторяется до тех пор, пока при проверке очередного результата не будет получено условие β*r≤ βr.
Если обрабатываемая выборка содержит большое количество результатов (n>> 20), когда при определении доверительного интервала используются табличные значения интеграла вероятности, то критерием для определения результатов, содержащих грубые погрешности, может быть, например, критерий β*r ≤ 3[2, 3].Таким образом, за границы допускаемых нормированных отклонений случайной погрешности в этом случае принимают границы максимальной случайной погрешности, а доверительная вероятность, при которой осуществляется исключение грубых погрешностей, Рдов = 0,997.
Последовательность выполнения работы
1. Вычертить эскиз детали с указанием контролируемого размера.
2. Выполнить измерения заданного размера в партии (30 шт.) деталей, полученные размеры занести в таблицу формы 1 с двумя столбцами: порядковый номер измерения; результат измерения.
3. Построить гистограмму по результатам измерений, оценить по виду гистограммы ее близость к закону нормального распределения.
4. Определить:
– оценку математического ожидания результата измерений X по формуле (1);
– оценку средней квадратической погрешности единичного измерения Sx по формуле (2).
5. Последовательно исключить резко выделяющиеся результаты измерений (с грубыми погрешностями), используя формулу (7) и условие β*r ≤ 3 при доверительной вероятности осуществления исключения грубых погрешностей Рдов = 0,997.
6. После каждого исключения единичной грубой погрешности выполнить перерасчет статистических оценок по п. 4.
7. Определить оценку средней квадратической погрешности оценки математического ожидания Sx по формуле (3).
8. Определить по формуле (4) границы симметричного доверительного интервала ±∆Хр, за границы которого с заданной доверительной вероятностью Рдов = 0,95 и Рдов = 0,99 не выходит случайная погрешность результата измерений. Значение безразмерного коэффициента t в формуле (4) при заданных вероятностях получить из таблицы 1 интеграла вероятности, задаваемого зависимостью (5)).
9. Представить действительное значение размера в виде
(X – ∆Хр) ≤ Xдст ≤ [(X + ∆Хр)]
или Xдст = X±∆Хр= X ±tрSx
10. Составить и защитить отчет по практической работе.
Форма 1 – Таблица результатов измерений
Содержание отчета по практической работе
Контрольные вопросы
Литература
1. ГОСТ 8.207–76. Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.– Режим доступа: http://gostexpert.ru/gost/gost-8207-76 (доступ свободный)
2. Эрастов, В.Э. Метрология, стандартизация и сертификация[Текст]: Учебн. пособие/ В.Э. Эрастов. – М.: ФОРУМ, 2008. – 205 с.
Практическая работа №3
Изучение и составление схем измерения погрешностей формы
и расположения поверхностей деталей
Цель работы
1. Закрепить теоретические знания по нормированию точности формы и расположения поверхностей деталей.
2. Изучить схемы измерений отклонений формы и расположения поверхностей деталей.
3. Получить навыки разработки схем измерения погрешности формы и расположения поверхностей деталей.
Пояснение к условию практической работы
В ходе выполнения практической работы изучаются приведенные в пособии схемы измерений отклонений формы и расположения, уровень изучения должен обеспечить самостоятельное объяснение каждой из приведенных схем.
Задание по теме практического занятия выдается на группу студентов из 3–4-х человек, оно включает выполнение и описание 3-4-х схем измерения отклонений формы и расположения из числа представленных ниже по тексту, а также чертеж детали достаточной сложности с нормируемыми по точности размерами, отклонениями формы и расположения поверхностей. Чертеж изучается, выявляются требования по точности размера и допускаемым отклонениям формы и расположения каждой из поверхностей детали. При этом должны быть учтены требования, размещенные на поле чертежа непосредственно на контуре детали, и требования приведенные в технических требованиях чертежа (над основной надписью).
Изучение и разработка схем измерения отклонений формы и расположения необходимы для осознанного понимания сущности решения точностных задач в технологии машиностроения и будущей профессиональной деятельности в этой области.
В описании настоящей практической работы приведен ряд применяемых способов и схем измерения отклонений форм и расположения (таких схем и способов их реализации в практике множество), что будет полезно для освоения этого весьма сложного материала в разделе «Нормирование точности» изучаемой дисциплины.
Практическая работа выполняется в соответствии с порядком, представленным ниже.
Для сознательного и качественного выполнения практической работы необходимо повторить материалы лекции по данной теме и внимательно изучить материалы, представленные ниже в рамках настоящего пособия.
Общие понятия нормирования точности формы и расположения поверхностей деталей
Для нормирования допусков на отклонения формы и расположения поверхностей введены ГОСТ 24642–81 [1] и ГОСТ 24643–81 [2].
В ГОСТ 24642–81 включены: пять видов отклонений (допусков) формы, семь видов отклонений (допусков) расположения и семь видов отклонений (допусков) суммарных отклонений формы и расположения. ГОСТ 24643–81 представляет числовые значения допусков формы и расположения, распределенных по 16 степеням точности и построенных по геометрической прогрессии с знаменателем 1,6 (ряд R5).
В основу нормирования и количественной оценки отклонений формы и расположения поверхностей положен принцип прилегающих прямых, поверхностей и профилей. При этом, как правило, шероховатость поверхности, полученная в результате механической обработки, не учитывается. При оценке отклонений расположения исключаются отклонения формы, в то же время при оценке суммарных отклонений формы и расположения они учитываются.
Прилегающая прямая – прямая соприкасающаяся с реальным профилем и расположенная вне материала детали так, чтобы отклонениеЕот нее наиболее удаленной точки реального профиля в пределах нормируемого участка имело минимальное значение (рисунок 1).
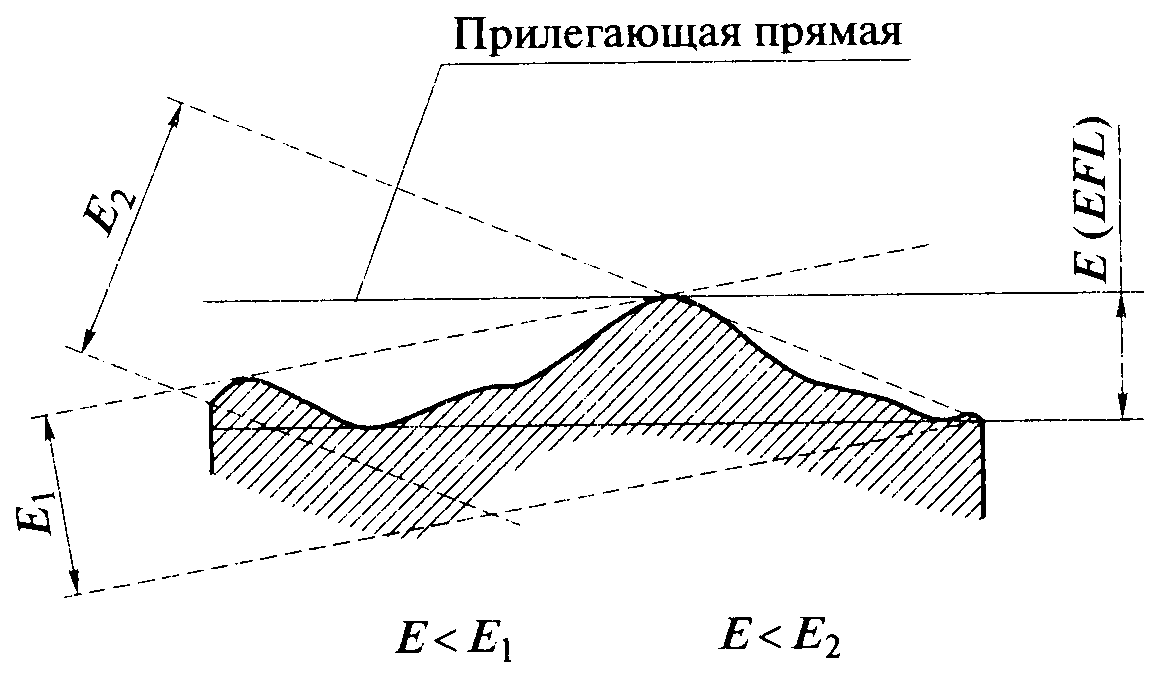
Рисунок 1 – Прилегающая прямая, отклонение от прямолинейности (EFL)
Соответствующее расположение имеет прилегающая плоскость относительно реальной поверхности и прилегающий профиль относительно реального профиля.
Прилегающая окружность – это окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения. Соответствующее расположение имеет прилегающий цилиндр относительно реальной поверхности вращения (рисунок 2).
β*r =(Xk – X) / Sx. (7)
Задав уровень доверительной вероятностиРдов находят табличное значениеβr для числа n, соответствующего обрабатываемой выборке. Если β*r>βr, то результат Xk можно отбросить, в противном случае результат должен быть оставлен.
После исключения результата, содержащего грубую погрешность, значения X и Sx уточняются, так как число результатов в выборке уменьшилось. Затем выполняется описанная выше процедура для результата выборки, имеющего наибольшее по модулю отклонение от уточненного значения X.Описанный порядок действия повторяется до тех пор, пока при проверке очередного результата не будет получено условие β*r≤ βr.
Если обрабатываемая выборка содержит большое количество результатов (n>> 20), когда при определении доверительного интервала используются табличные значения интеграла вероятности, то критерием для определения результатов, содержащих грубые погрешности, может быть, например, критерий β*r ≤ 3[2, 3].Таким образом, за границы допускаемых нормированных отклонений случайной погрешности в этом случае принимают границы максимальной случайной погрешности, а доверительная вероятность, при которой осуществляется исключение грубых погрешностей, Рдов = 0,997.
Последовательность выполнения работы
1. Вычертить эскиз детали с указанием контролируемого размера.
2. Выполнить измерения заданного размера в партии (30 шт.) деталей, полученные размеры занести в таблицу формы 1 с двумя столбцами: порядковый номер измерения; результат измерения.
3. Построить гистограмму по результатам измерений, оценить по виду гистограммы ее близость к закону нормального распределения.
4. Определить:
– оценку математического ожидания результата измерений X по формуле (1);
– оценку средней квадратической погрешности единичного измерения Sx по формуле (2).
5. Последовательно исключить резко выделяющиеся результаты измерений (с грубыми погрешностями), используя формулу (7) и условие β*r ≤ 3 при доверительной вероятности осуществления исключения грубых погрешностей Рдов = 0,997.
6. После каждого исключения единичной грубой погрешности выполнить перерасчет статистических оценок по п. 4.
7. Определить оценку средней квадратической погрешности оценки математического ожидания Sx по формуле (3).8. Определить по формуле (4) границы симметричного доверительного интервала ±∆Хр, за границы которого с заданной доверительной вероятностью Рдов = 0,95 и Рдов = 0,99 не выходит случайная погрешность результата измерений. Значение безразмерного коэффициента t в формуле (4) при заданных вероятностях получить из таблицы 1 интеграла вероятности, задаваемого зависимостью (5)).
9. Представить действительное значение размера в виде
(X – ∆Хр) ≤ Xдст ≤ [(X + ∆Хр)]
или Xдст = X±∆Хр= X ±tрSx
10. Составить и защитить отчет по практической работе.
Форма 1 – Таблица результатов измерений
| № изм. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Хi | | | | | | | | | | |
 Хi – X | | | | | | | | | | |
| № изм. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Хi | | | | | | | | | | |
| Хi – X | | | | | | | | | | |
| № изм. | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Хi | | | | | | | | | | |
| Хi – X | | | | | | | | | | |
Содержание отчета по практической работе
-
Цель практической работы -
Методика измерений -
Схема измерения -
Эскиз детали с указанием измеряемого размера -
Результаты измерений в табличной форме -
Построение гистограммы -
Статистическая обработка результатов измерений с исключением грубых погрешностей. -
Записать границы доверительного интервала (рдов = 0,95 и рдов = 0,97) для оценки действительного значения размера Х
Контрольные вопросы
-
Дайте понятие систематической, случайной и грубой погрешности измерения. -
Какие числовые характеристики являются основными для нормального закона распределения? -
Каким образом связаны числовые характеристики точности проведенных измерений – дисперсия и средняя квадратическая погрешность (СКП)? -
Каким образом проявляется влияние числовых характеристик на положение и форму кривых функции нормального распределения? -
В чем состоит различие между теоретическими значениями числовых характеристик распределения и их оценками? -
Какие понятия стоят за обозначениями σ[Х],Sx, Sx, что общего в этих понятиях? -
Что такое точечные оценки числовых характеристик законов распределения? -
Что такое средняя квадратическая погрешность среднего арифметического? -
Объясните понятия доверительный интервал, доверительная вероятность. -
Как используются понятия «доверительный интервал» и «доверительная вероятность» в представлении действительного результата измерений? -
Как выражаются границы симметричного доверительного интервала? -
С какой целью применяют нормированную функцию Лапласа? -
Что вы знаете о статистическом критерии обнаружения грубых погрешностей? -
Как строится гистограмма результатов измерений, в чем ее практическая ценность?
Литература
1. ГОСТ 8.207–76. Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.– Режим доступа: http://gostexpert.ru/gost/gost-8207-76 (доступ свободный)
2. Эрастов, В.Э. Метрология, стандартизация и сертификация[Текст]: Учебн. пособие/ В.Э. Эрастов. – М.: ФОРУМ, 2008. – 205 с.
Практическая работа №3
Изучение и составление схем измерения погрешностей формы
и расположения поверхностей деталей
Цель работы
1. Закрепить теоретические знания по нормированию точности формы и расположения поверхностей деталей.
2. Изучить схемы измерений отклонений формы и расположения поверхностей деталей.
3. Получить навыки разработки схем измерения погрешности формы и расположения поверхностей деталей.
Пояснение к условию практической работы
В ходе выполнения практической работы изучаются приведенные в пособии схемы измерений отклонений формы и расположения, уровень изучения должен обеспечить самостоятельное объяснение каждой из приведенных схем.
Задание по теме практического занятия выдается на группу студентов из 3–4-х человек, оно включает выполнение и описание 3-4-х схем измерения отклонений формы и расположения из числа представленных ниже по тексту, а также чертеж детали достаточной сложности с нормируемыми по точности размерами, отклонениями формы и расположения поверхностей. Чертеж изучается, выявляются требования по точности размера и допускаемым отклонениям формы и расположения каждой из поверхностей детали. При этом должны быть учтены требования, размещенные на поле чертежа непосредственно на контуре детали, и требования приведенные в технических требованиях чертежа (над основной надписью).
Изучение и разработка схем измерения отклонений формы и расположения необходимы для осознанного понимания сущности решения точностных задач в технологии машиностроения и будущей профессиональной деятельности в этой области.
В описании настоящей практической работы приведен ряд применяемых способов и схем измерения отклонений форм и расположения (таких схем и способов их реализации в практике множество), что будет полезно для освоения этого весьма сложного материала в разделе «Нормирование точности» изучаемой дисциплины.
Практическая работа выполняется в соответствии с порядком, представленным ниже.
Для сознательного и качественного выполнения практической работы необходимо повторить материалы лекции по данной теме и внимательно изучить материалы, представленные ниже в рамках настоящего пособия.
Общие понятия нормирования точности формы и расположения поверхностей деталей
Для нормирования допусков на отклонения формы и расположения поверхностей введены ГОСТ 24642–81 [1] и ГОСТ 24643–81 [2].
В ГОСТ 24642–81 включены: пять видов отклонений (допусков) формы, семь видов отклонений (допусков) расположения и семь видов отклонений (допусков) суммарных отклонений формы и расположения. ГОСТ 24643–81 представляет числовые значения допусков формы и расположения, распределенных по 16 степеням точности и построенных по геометрической прогрессии с знаменателем 1,6 (ряд R5).
В основу нормирования и количественной оценки отклонений формы и расположения поверхностей положен принцип прилегающих прямых, поверхностей и профилей. При этом, как правило, шероховатость поверхности, полученная в результате механической обработки, не учитывается. При оценке отклонений расположения исключаются отклонения формы, в то же время при оценке суммарных отклонений формы и расположения они учитываются.
Прилегающая прямая – прямая соприкасающаяся с реальным профилем и расположенная вне материала детали так, чтобы отклонениеЕот нее наиболее удаленной точки реального профиля в пределах нормируемого участка имело минимальное значение (рисунок 1).
Рисунок 1 – Прилегающая прямая, отклонение от прямолинейности (EFL)
Соответствующее расположение имеет прилегающая плоскость относительно реальной поверхности и прилегающий профиль относительно реального профиля.
Прилегающая окружность – это окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения. Соответствующее расположение имеет прилегающий цилиндр относительно реальной поверхности вращения (рисунок 2).