Файл: Методические указания и задания к курсовому проектированию для студентов специальности Радиотехника Екатеринбург 2022 удк 621. 396.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 103
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
стержне не возбуждались высшие типы волн, искажающие диаграмму направленности антенны, необходимо выполнить соотношение:
.
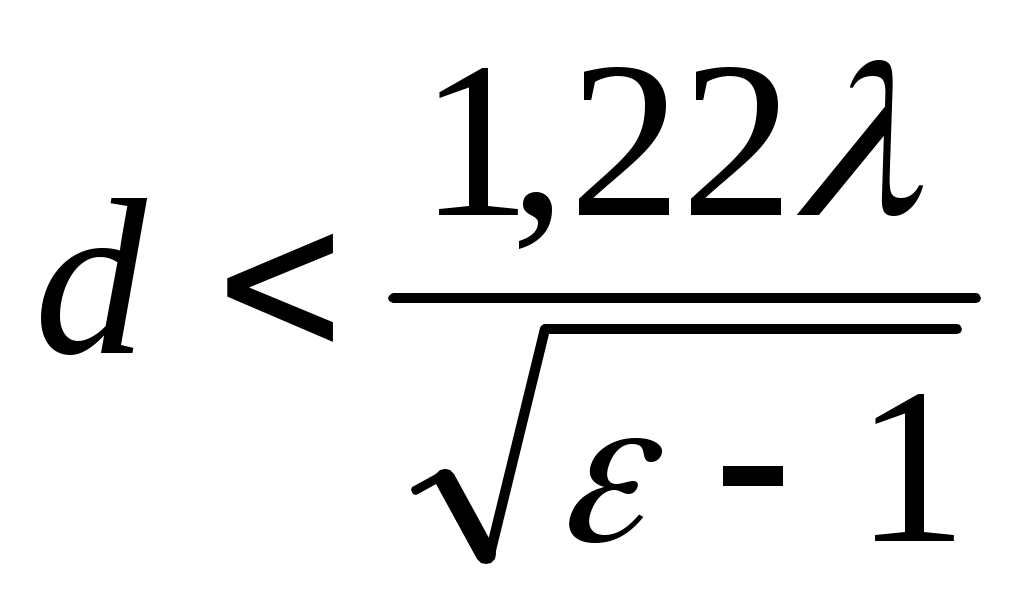1.4 Спиральные антенны
Спиральная антенна (1.7) состоит из проволочной спирали, питаемой коаксиальной линией, внутренний проводник которой присоединен к спирали, а наружный - к металлическому диску – рефлектору, который ослабляет излучение поля в заднее полупространство.
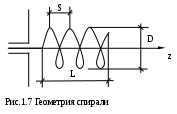
Диаметр диска выбирается (0,8-1,5)L, где L –длина спирали. Длина витка спирали l связана с шагом спирали Sсоотношением S/l=sinγ, γ – угол подъема витка спирали.
Основное применение находят спирали с максимумом излучения вдоль оси при круговой или эллиптической поляризации в направлении максимального излучения. Для получения поля круговой поляризации связь между l и S выбирается в соответствии с формулой:
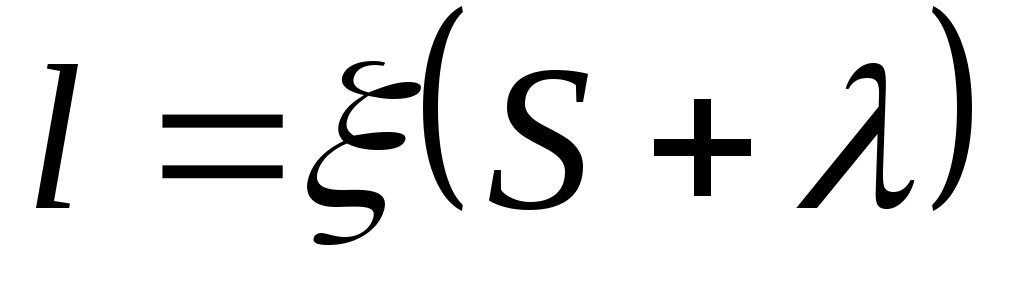, (1.8)
где
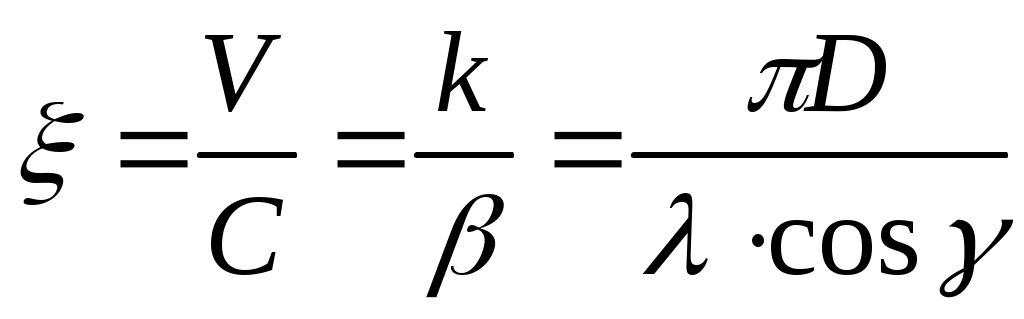- коэффициент замедления.
Диаграмма направленности цилиндрической спирали в угломестной плоскости рассчитывается по формуле:
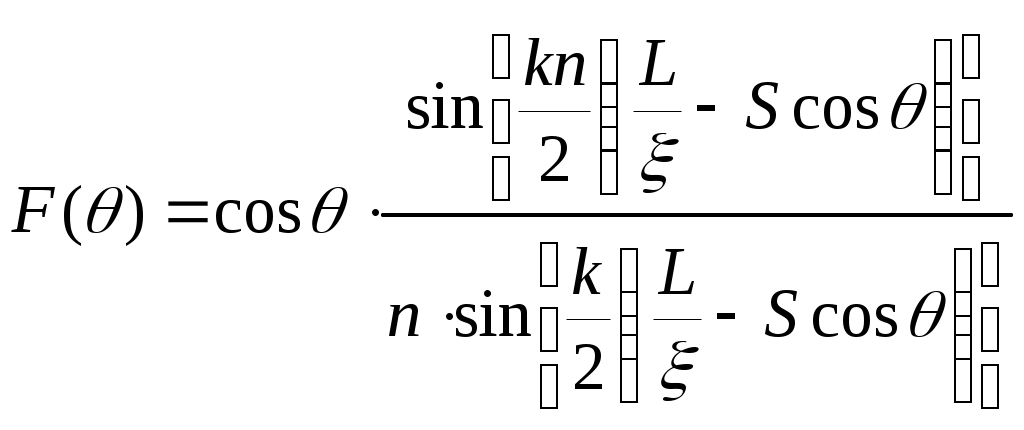, (1.9)
где n – число витков в спирали.
Ширина ДН по уровню половинной мощности равна:
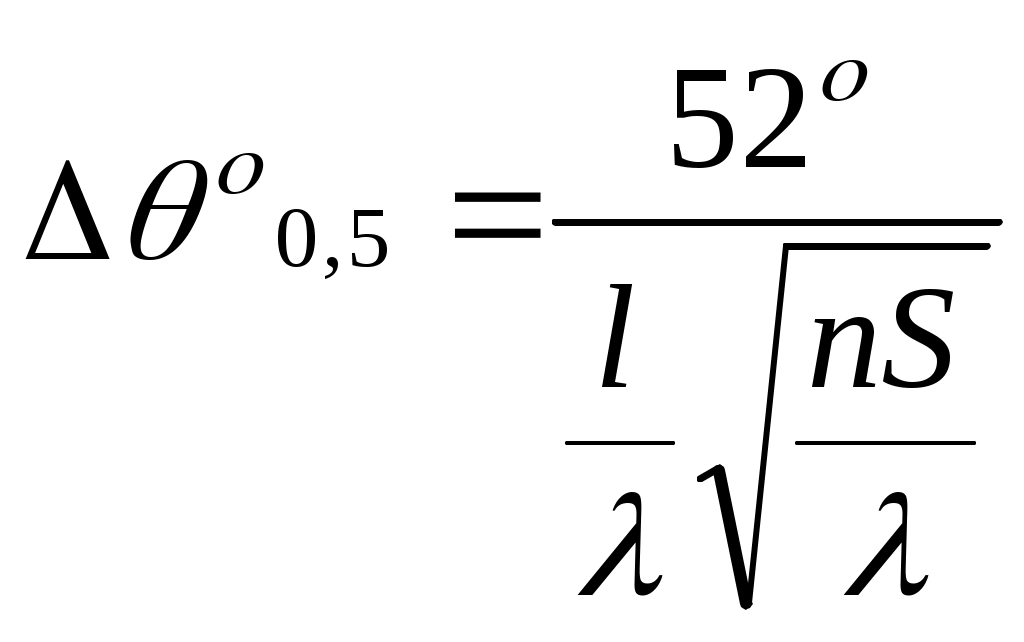. (1.10)
Формула для КНД в направлении максимального излучения имеет вид:
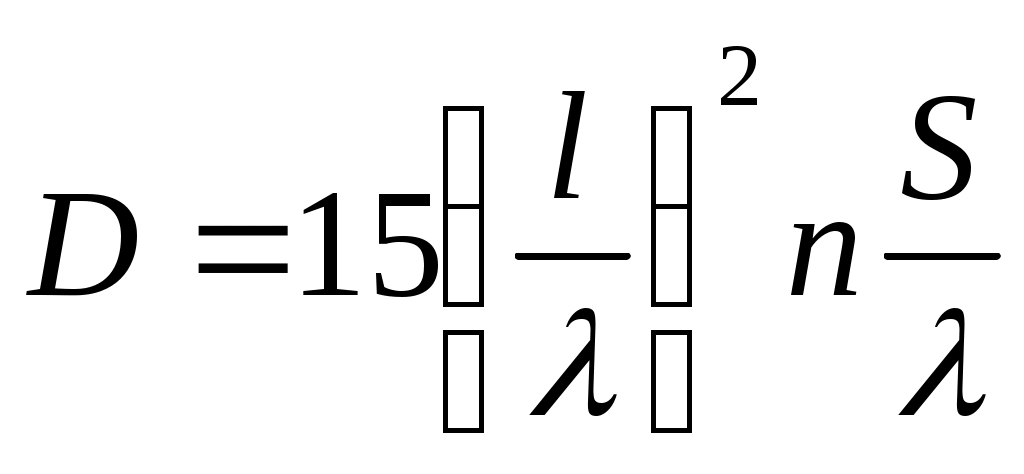. (1.11)
Входное сопротивление:
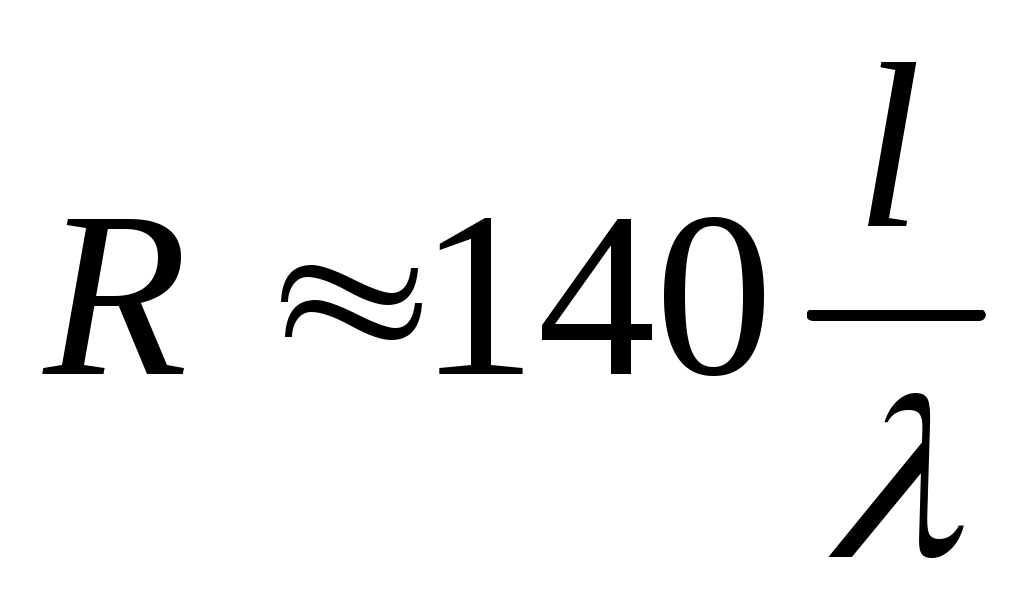[Ом]. (1.12)
Коэффициент эллиптичности в направлении оси z определяется как:
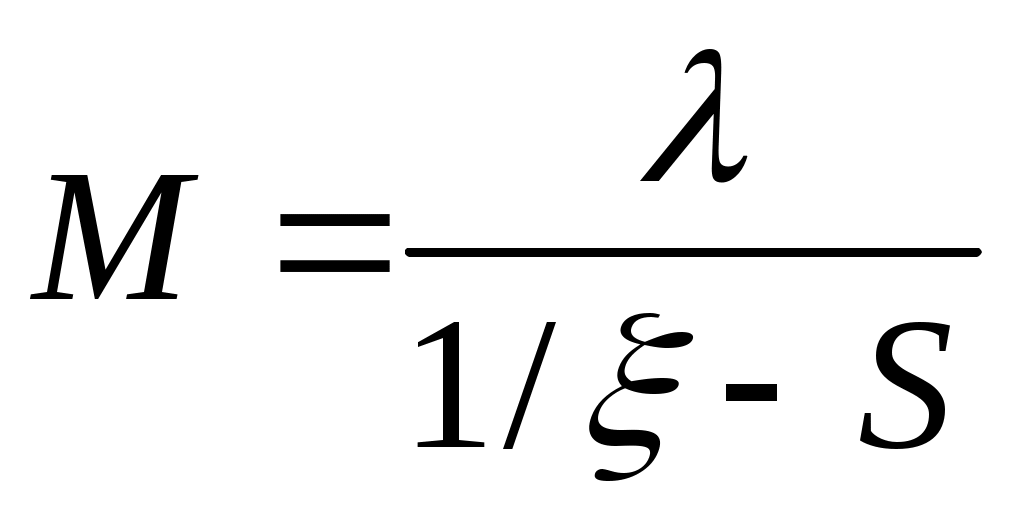. (1.13)
Формулы (1.10) – (1.13) применимы при условии, когда n>3, 12º≤γ≤16º. Для других значений n и γ необходимо использовать более точные соотношения из [2].
1.5 Полосковые антенны
Такие антенны находят широкое применение в ДМ и СМ диапазонах и обычно выполняются по технологиям печатных интегральных схем. Они отличаются малой массой и габаритами, высокой точностью изготовления и повторяемостью размеров, что обеспечивает хорошую воспроизводимость характеристик, удобством возбуждения полосковыми или коаксиальными линиями.
В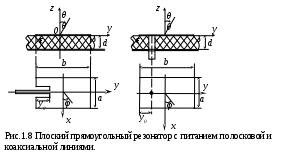
настоящее время применяется большое число типов полосковых антенн, но наиболее распространенными являются резонаторные, вибраторные и щелевые. На рис. 1.8 приведены эскизы прямоугольных резонаторных антенн при возбуждении их полосковой и коаксиальной линиями. Для согласования точка питания смещена на размер y0 от края резонатора.
Края резонатора, в свою очередь, образуют две излучающие щели длиной a, располагающиеся на расстоянии b. Если выбирать размер b≈λρ/2, где λρ – длина волны в полосковой линии шириной a, образующей резонатор, то нормальные проводящей подложке составляющие электрического поля щелей будут противофазны и вычитаться, а параллельные ей – синфазны и складываться. Последние две составляющие образуют поле излучения резонаторной антенны. Поляризация его линейна, а максимум ориентирован в направлении нормали к плоскости резонатора (θ=0º) .
Размер резонатора - а может быть различным и влияет, в первую очередь, на величину входного сопротивления. Кроме этого, длина излучающей щели с равномерным по амплитуде распределением поля определяет диаграмму направленности резонаторной антенны в плоскости xoz.
Для получения поля вращающейся поляризации необходимы две пары одинаковых излучающих щелей, расположенные перпендикулярно друг другу и возбуждаемые со сдвигом по фазе на π/2. Это может быть получено с помощью квадратного резонатора, питаемого в двух точках в серединах соседних сторон, хотя возможны и другие способы [3].
Входное сопротивление на резонансной частоте для прямоугольного резонатора чисто активно и определяется формулой:
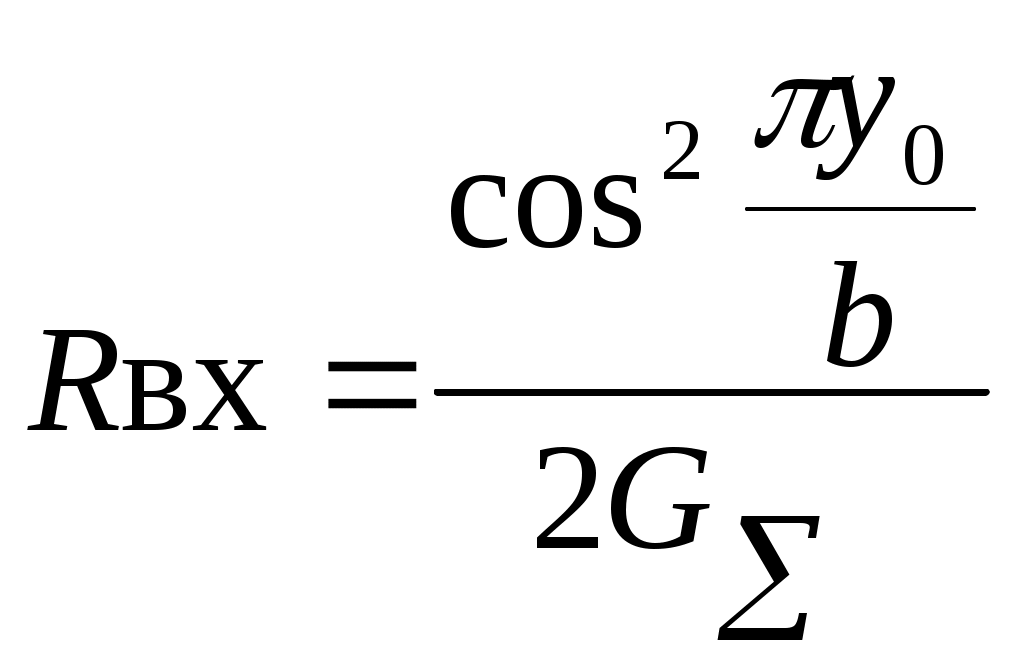, (1.14)
где GΣ – проводимость излучения торцевой щели резонатора длинной а. Она определяется соотношением:
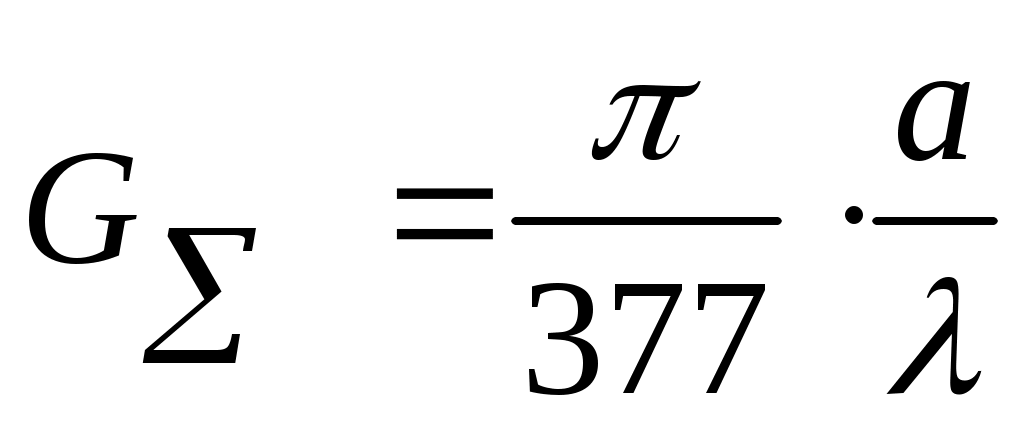[Сим]. (1.15)
Резонансная длина антенны
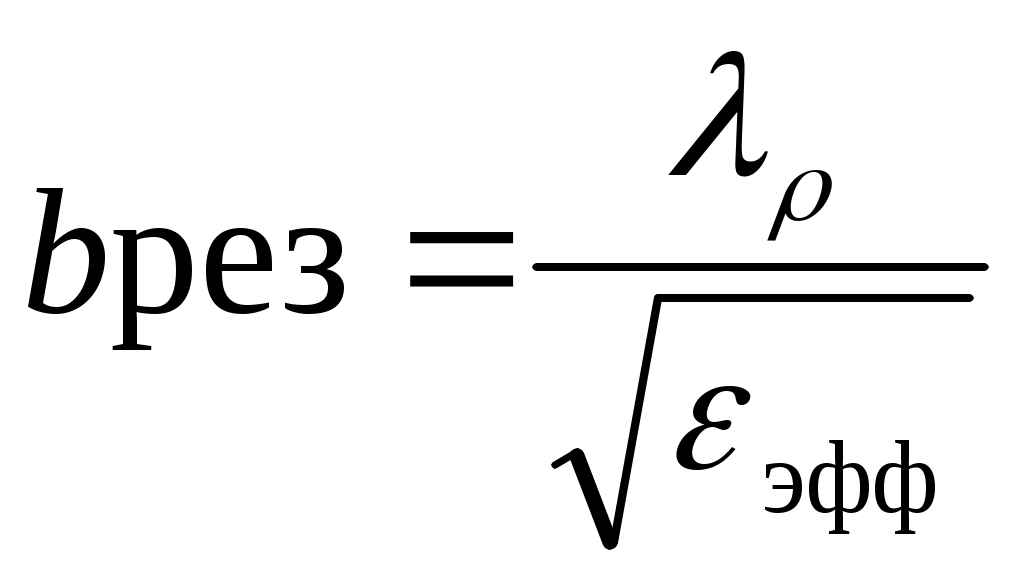, (1.16)
где
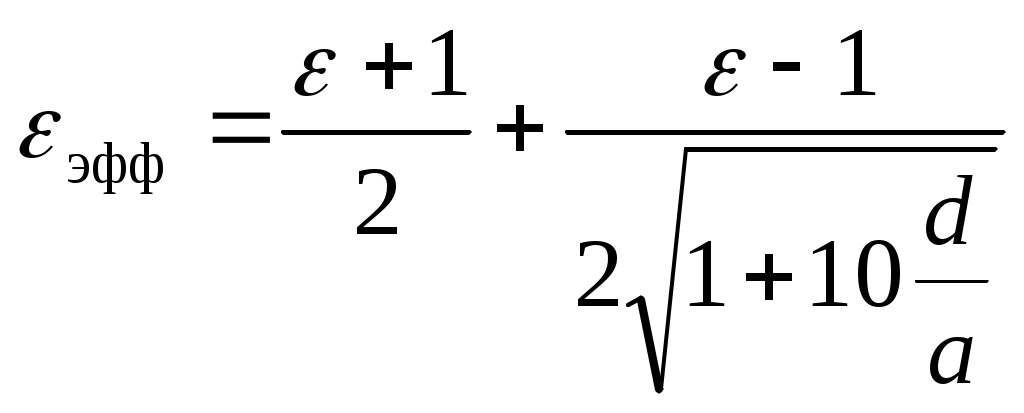(1.17)
- эффективная диэлектрическая проницаемость полосковой линии шириной
а, λρ – резонансная длина волны. Для прикидочных расчетов обычно можно использовать соотношение
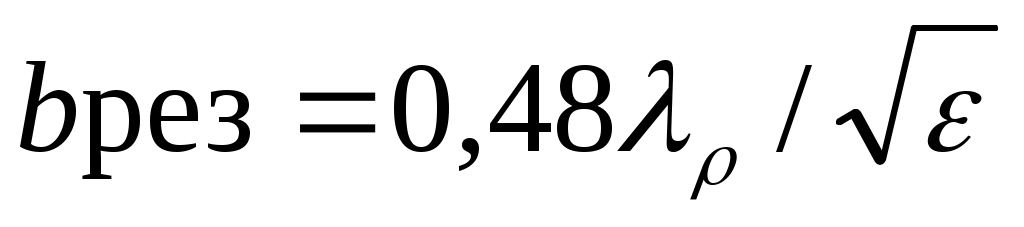. (1.18)
Диаграмма направленности рассчитывается по формуле:
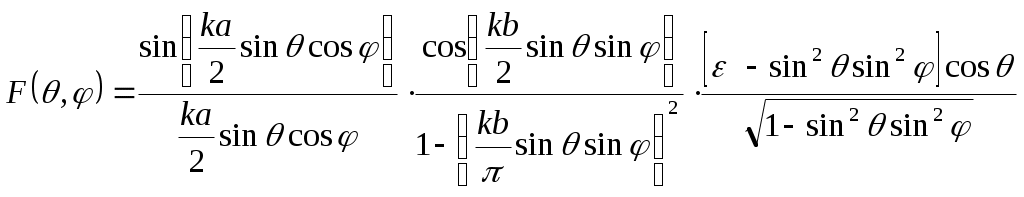(1.19)
и имеет один максимум по нормали к резонатору (θmax=0º).
Расчет полосковой резонаторной антенны обычно начинают с выбора размера а щели по заданной характеристике направленности. При этом размер b берут из приближенного соотношения. Необходимо учитывать, что от размера а зависит волновое сопротивление полосковой линии, из которой выполнен резонатор. Оно должно быть не слишком малым. Обычно его выбирают 10÷20 Ом, а рассчитывают, при а>>d, по формуле:
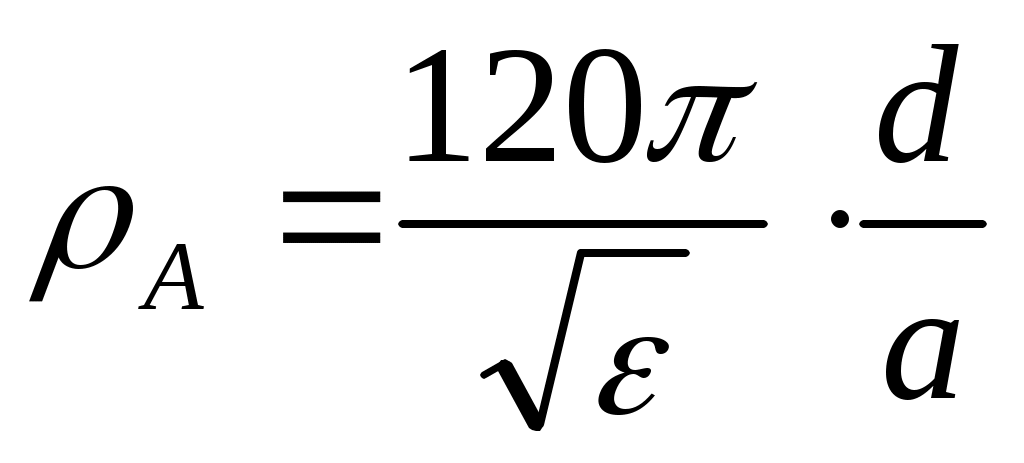[Ом]. (1.20)
Рекомендуемый размер а≈(0,3÷0,7)λ. Подложку, по тем же причинам, целесообразно выбирать с диэлектрической проницаемостью ε≈2,0÷2,5 (неполярные полимерные диэлектрики). В некоторых случаях для уменьшения габаритов резонатора можно взять подложку с ε от 5 до 10 (стеклотекстолиты, СВЧ пластмассы, керамика). Толщина подложки должна удовлетворять условию d<0,1λ.
При удовлетворении характеристик направленности спроектированной антенны рассчитывают bрез по формуле 1.16 и y0 по 1.14 и 1.15. При этом необходимо учитывать, что полосковые или коаксиальные линии, используемые для питания антенн, обычно имеют волновое сопротивление ρл=50 Ом.
Полосковые вибраторные антенны используют диэлектрик как конструктивный элемент с малыми потерями, поэтому диэлектрический слой выбирают тонким. Большое разнообразие вибраторных антенн в основном объясняется различиями в способах питания. Можно выделить две основные разновидности, приведенные на рис. 1.9.
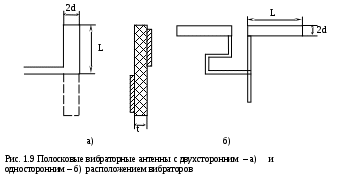
В обеих разновидностях обычно используются полуволновые вибраторы, поэтому L=λ/4. Размер 2d, который эквивалентен удвоенному диаметру проволочного вибратора равному 2ρ (см. рис. 1.1), должен удовлетворять условию 2d≤0,1λ. Другим условием является L/d≥5, так как в противном случае у диаграммы направленности «заплывают» нули (из-за излучения торцов вибраторов). Это является недопустимым при использовании вибраторов в качестве элементов решетки из-за увеличения связи между элементами и появления кроссполяризационной (ортогональной) составляющей излученного поля. Диэлектрическая пластина выбирается по возможности тонкой (t<0,1λ), так как в противном случае необходимо корректировать резонансную длину вибратора L
рез и возрастают диэлектрические потери. Для обеспечения одностороннего излучения вибраторы располагаются над проводящим экраном.
При обеспечении перечисленных ранее условий, характеристики направленности и входное сопротивление полоскового вибратора можно определить по соотношениям для проволочного вибратора (см. параграф 1.1). Для этого нужно брать 2ρ=2d/2=d, что обеспечивает эквивалентность цилиндрического и плоского вибратора.
Возбуждение печатных вибраторов может осуществляться коаксиальной линией с симметрирующим устройством или симметричной полосковой линией. Часто используется питание несимметричной полосковой линией, что особенно удобно для «односторонних» вибраторов (рис. 1.9 б). При этом плечи вибратора должны иметь сдвиг по питанию на π (разность длин питающих линий λл/2) для обеспечения синфазности токов.
Щелевые полосковые антенны примеряются в том же частотном диапазоне и в тех же целях, что и волноводно-щелевые антенны. Главным их преимуществом является малая дисперсия полосковой линии передачи, а недостатком повышенные требования к ее коэффициенту затухания, особенно при большой длине антенной решетки.
Обычно щелевые излучатели прорезаются в одном из внешних проводников симметричной полосковой линии. Длина щели вычисляется по формуле:
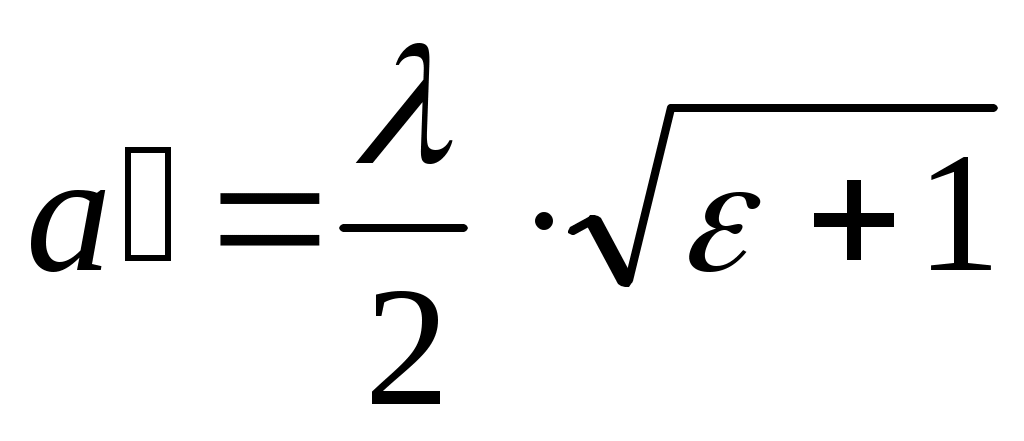, (1.21)
где ε – относительная диэлектрическая проницаемость диэлектрика симметричной полосковой линии, λ – длина волны в свободном пространстве.
Расчетная длина щели уточняется экспериментально, так как на значение
оказывают влияние высшие типы волн в полосковой линии и поверхностные волны, которые возбуждаются щелью на много эффективнее чем полосковым вибратором.
Для небольших решеток (число элементов N<10) используют или последовательное или параллельное питание щелей. Связь щели с полосковой линией регулируется смещением щели относительно проводника линии. Щель всегда перпендикулярна полосковой линии. В решетках большой длины щели возбуждаются бегущей волной тока. Возможно возбуждение и стоячей волной.
1.6 Рупорные антенны
В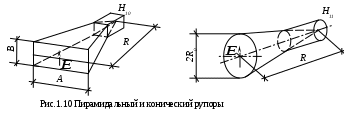
сантиметровом и миллиметровом диапазонах волн широко применяются пирамидальные и конические рупорные антенны (рис.1.10).
Пирамидальные рупоры возбуждаются прямоугольным волноводом, конические – круглым или, через плавный переход, прямоугольным. Если размер рупора В=b - ширине узкой стенки прямоугольного волновода, а размер А произвольный, рупор называется Н-секториальным (расширяется в плоскости вектора
). Если расширение делается только в плоскости вектора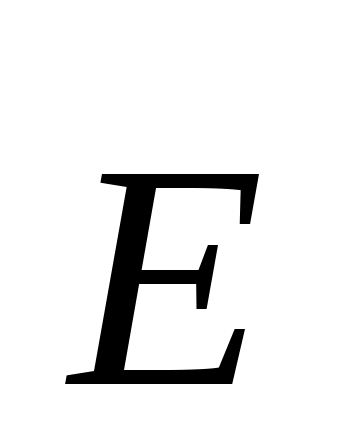 
(А=а – широкой стенке волновода), то рупор Е-секториальный. При расширении в обеих плоскостях – пирамидальный рупор.
Диаграмма направленности рупорной антенны определяется амплитудным и фазовым распределением поля в ее раскрыве. При небольших углах раскрыва рупора и при проведении оценочных расчетов ширины главного лепестка фазовыми искажениями можно пренебречь и воспользоваться данными табл. 3.1.
Размеры оптимального прямоугольного рупора связаны следующими соотношениями:
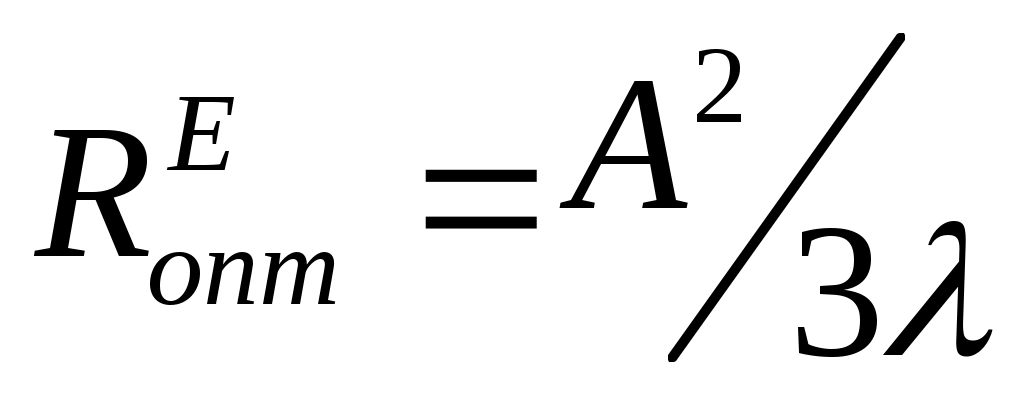
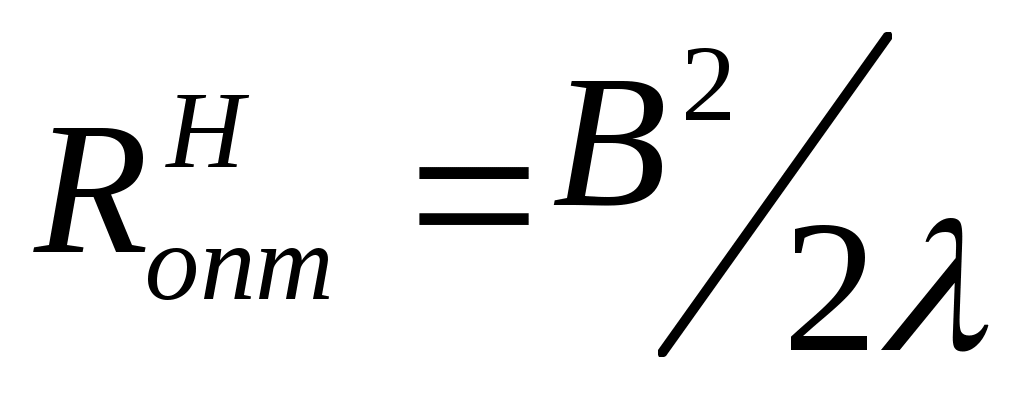
где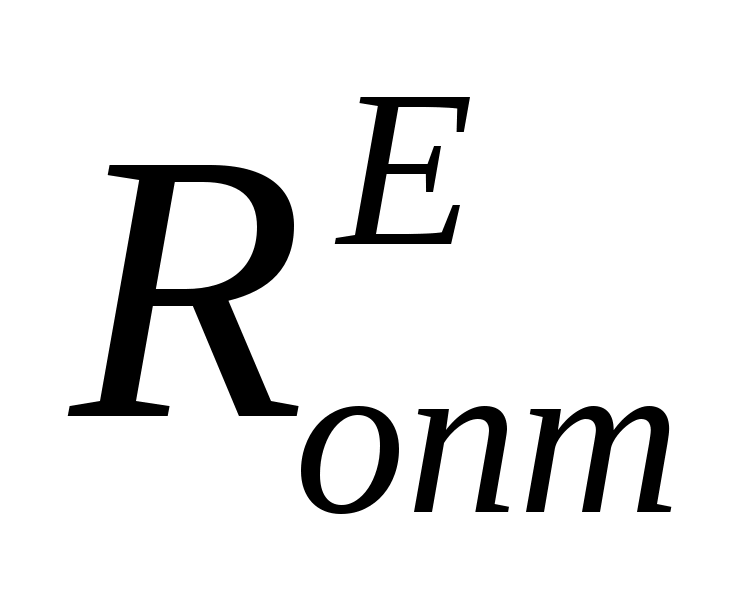
и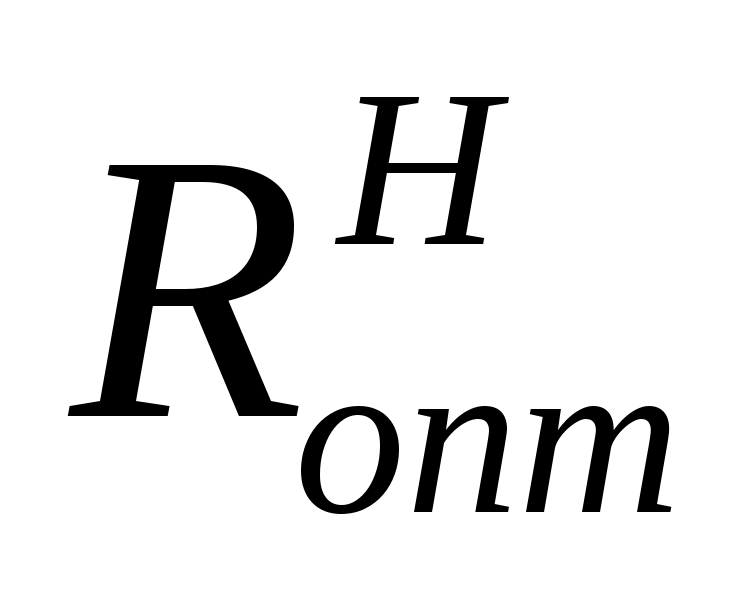 
- длина оптимального рупора соответственно в плоскостях векторов Е и Н. Если 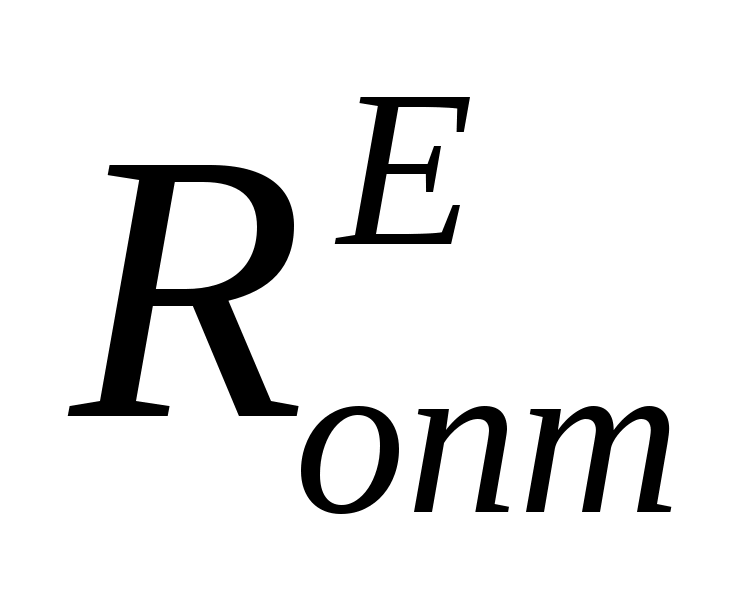≠ 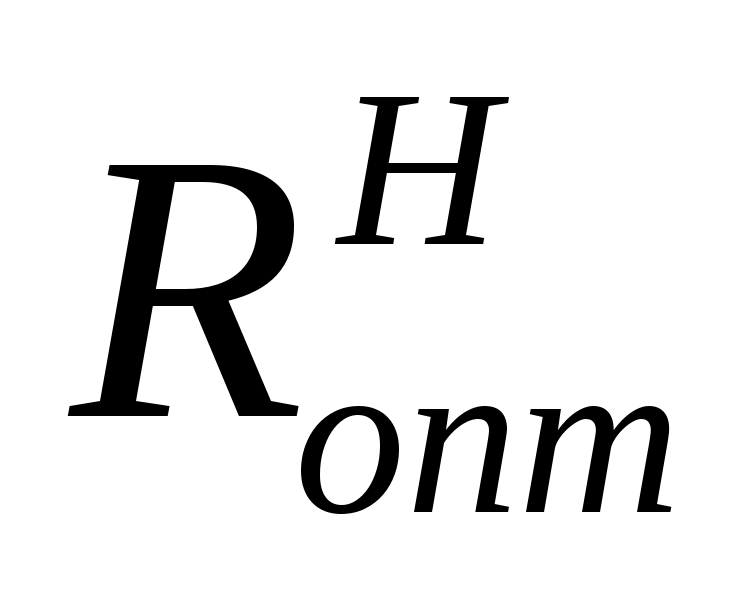, то длина рупора R выбирается равной большему значению из них.
Ширина главного лепестка диаграммы направленности оптимального прямоугольного рупора по уровню половинной мощности в плоскости вектора определяется по эмпирической формуле:
,
а в плоскости вектора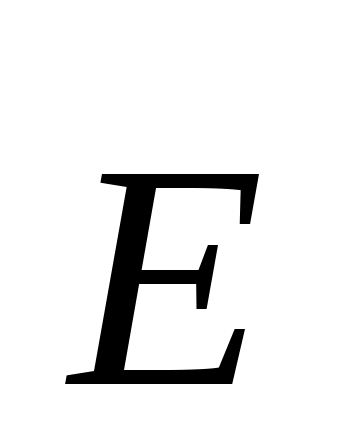
.1.4 Спиральные антенны
Спиральная антенна (1.7) состоит из проволочной спирали, питаемой коаксиальной линией, внутренний проводник которой присоединен к спирали, а наружный - к металлическому диску – рефлектору, который ослабляет излучение поля в заднее полупространство.
Диаметр диска выбирается (0,8-1,5)L, где L –длина спирали. Длина витка спирали l связана с шагом спирали Sсоотношением S/l=sinγ, γ – угол подъема витка спирали.
Основное применение находят спирали с максимумом излучения вдоль оси при круговой или эллиптической поляризации в направлении максимального излучения. Для получения поля круговой поляризации связь между l и S выбирается в соответствии с формулой:
, (1.8)где
- коэффициент замедления.Диаграмма направленности цилиндрической спирали в угломестной плоскости рассчитывается по формуле:
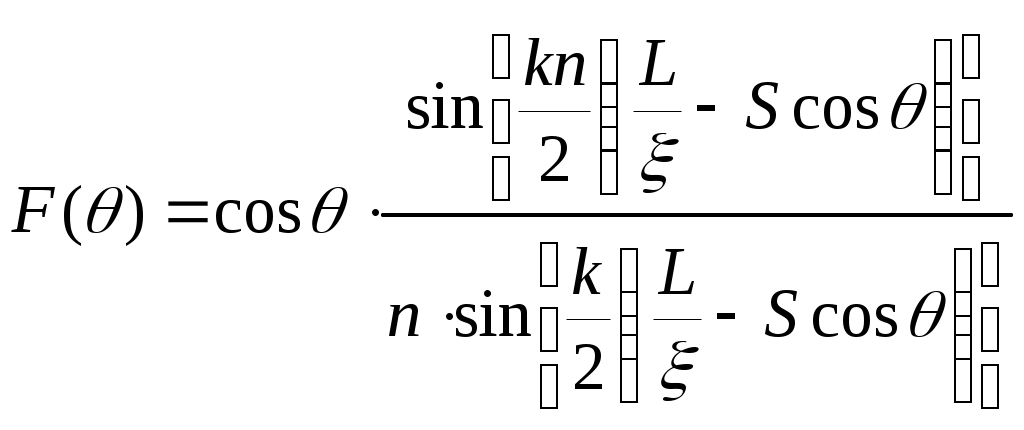, (1.9)где n – число витков в спирали.
Ширина ДН по уровню половинной мощности равна:
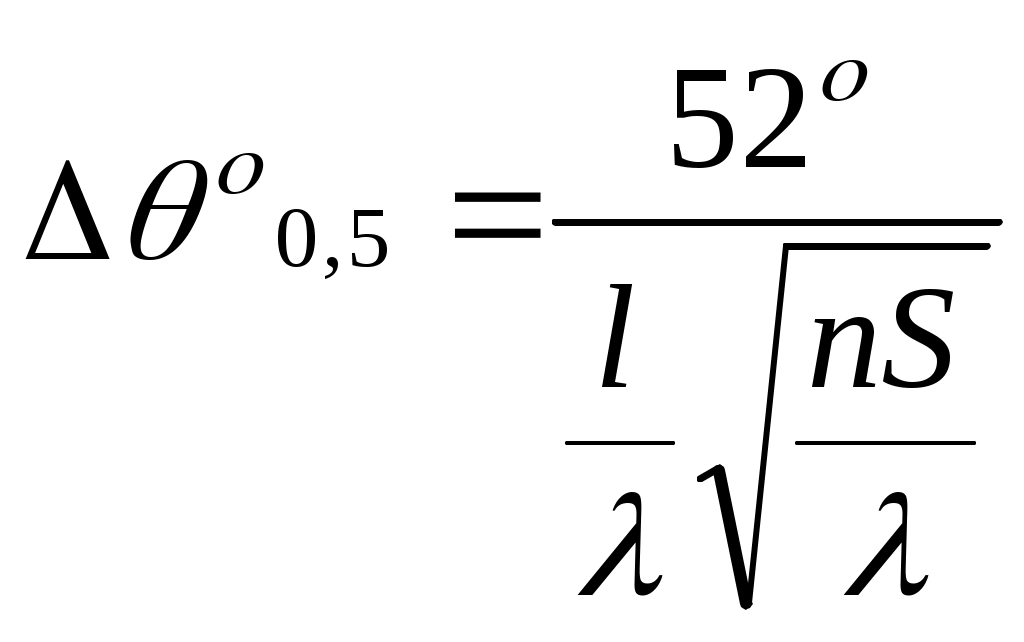. (1.10)Формула для КНД в направлении максимального излучения имеет вид:
. (1.11)Входное сопротивление:
[Ом]. (1.12)Коэффициент эллиптичности в направлении оси z определяется как:
. (1.13)Формулы (1.10) – (1.13) применимы при условии, когда n>3, 12º≤γ≤16º. Для других значений n и γ необходимо использовать более точные соотношения из [2].
1.5 Полосковые антенны
Такие антенны находят широкое применение в ДМ и СМ диапазонах и обычно выполняются по технологиям печатных интегральных схем. Они отличаются малой массой и габаритами, высокой точностью изготовления и повторяемостью размеров, что обеспечивает хорошую воспроизводимость характеристик, удобством возбуждения полосковыми или коаксиальными линиями.
В
настоящее время применяется большое число типов полосковых антенн, но наиболее распространенными являются резонаторные, вибраторные и щелевые. На рис. 1.8 приведены эскизы прямоугольных резонаторных антенн при возбуждении их полосковой и коаксиальной линиями. Для согласования точка питания смещена на размер y0 от края резонатора.Края резонатора, в свою очередь, образуют две излучающие щели длиной a, располагающиеся на расстоянии b. Если выбирать размер b≈λρ/2, где λρ – длина волны в полосковой линии шириной a, образующей резонатор, то нормальные проводящей подложке составляющие электрического поля щелей будут противофазны и вычитаться, а параллельные ей – синфазны и складываться. Последние две составляющие образуют поле излучения резонаторной антенны. Поляризация его линейна, а максимум ориентирован в направлении нормали к плоскости резонатора (θ=0º) .
Размер резонатора - а может быть различным и влияет, в первую очередь, на величину входного сопротивления. Кроме этого, длина излучающей щели с равномерным по амплитуде распределением поля определяет диаграмму направленности резонаторной антенны в плоскости xoz.
Для получения поля вращающейся поляризации необходимы две пары одинаковых излучающих щелей, расположенные перпендикулярно друг другу и возбуждаемые со сдвигом по фазе на π/2. Это может быть получено с помощью квадратного резонатора, питаемого в двух точках в серединах соседних сторон, хотя возможны и другие способы [3].
Входное сопротивление на резонансной частоте для прямоугольного резонатора чисто активно и определяется формулой:
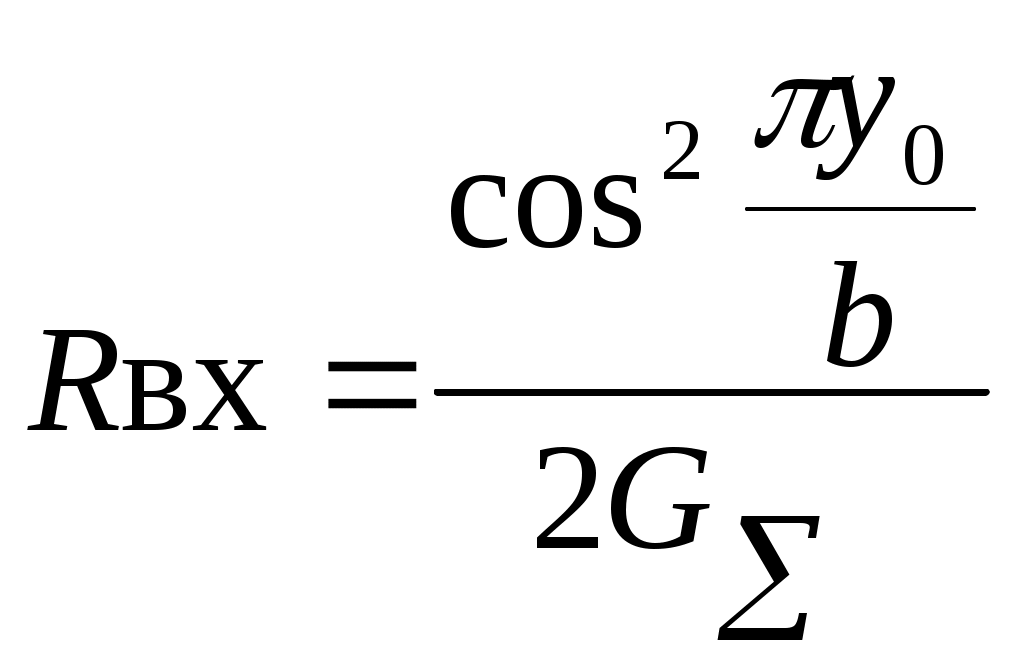, (1.14)где GΣ – проводимость излучения торцевой щели резонатора длинной а. Она определяется соотношением:
[Сим]. (1.15)Резонансная длина антенны
, (1.16)где
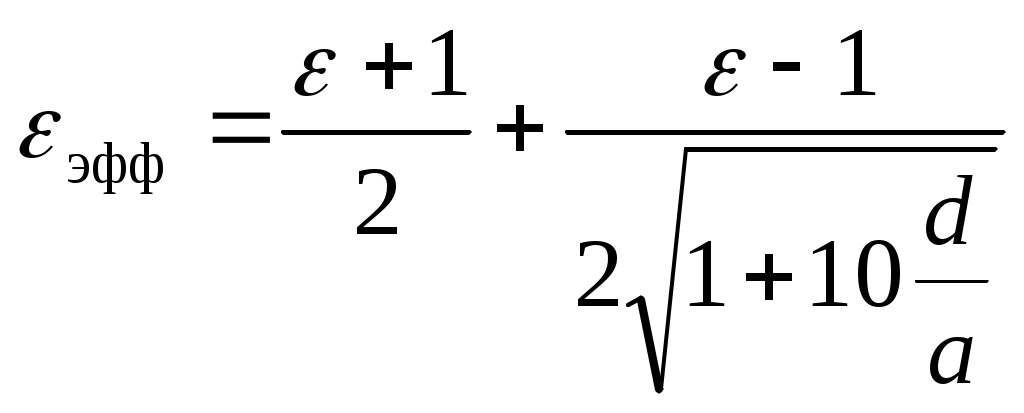(1.17)- эффективная диэлектрическая проницаемость полосковой линии шириной
а, λρ – резонансная длина волны. Для прикидочных расчетов обычно можно использовать соотношение
. (1.18)Диаграмма направленности рассчитывается по формуле:
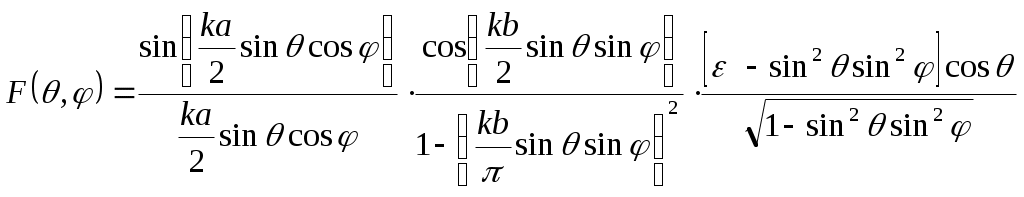(1.19)и имеет один максимум по нормали к резонатору (θmax=0º).
Расчет полосковой резонаторной антенны обычно начинают с выбора размера а щели по заданной характеристике направленности. При этом размер b берут из приближенного соотношения. Необходимо учитывать, что от размера а зависит волновое сопротивление полосковой линии, из которой выполнен резонатор. Оно должно быть не слишком малым. Обычно его выбирают 10÷20 Ом, а рассчитывают, при а>>d, по формуле:
[Ом]. (1.20)Рекомендуемый размер а≈(0,3÷0,7)λ. Подложку, по тем же причинам, целесообразно выбирать с диэлектрической проницаемостью ε≈2,0÷2,5 (неполярные полимерные диэлектрики). В некоторых случаях для уменьшения габаритов резонатора можно взять подложку с ε от 5 до 10 (стеклотекстолиты, СВЧ пластмассы, керамика). Толщина подложки должна удовлетворять условию d<0,1λ.
При удовлетворении характеристик направленности спроектированной антенны рассчитывают bрез по формуле 1.16 и y0 по 1.14 и 1.15. При этом необходимо учитывать, что полосковые или коаксиальные линии, используемые для питания антенн, обычно имеют волновое сопротивление ρл=50 Ом.
Полосковые вибраторные антенны используют диэлектрик как конструктивный элемент с малыми потерями, поэтому диэлектрический слой выбирают тонким. Большое разнообразие вибраторных антенн в основном объясняется различиями в способах питания. Можно выделить две основные разновидности, приведенные на рис. 1.9.
В обеих разновидностях обычно используются полуволновые вибраторы, поэтому L=λ/4. Размер 2d, который эквивалентен удвоенному диаметру проволочного вибратора равному 2ρ (см. рис. 1.1), должен удовлетворять условию 2d≤0,1λ. Другим условием является L/d≥5, так как в противном случае у диаграммы направленности «заплывают» нули (из-за излучения торцов вибраторов). Это является недопустимым при использовании вибраторов в качестве элементов решетки из-за увеличения связи между элементами и появления кроссполяризационной (ортогональной) составляющей излученного поля. Диэлектрическая пластина выбирается по возможности тонкой (t<0,1λ), так как в противном случае необходимо корректировать резонансную длину вибратора L
рез и возрастают диэлектрические потери. Для обеспечения одностороннего излучения вибраторы располагаются над проводящим экраном.
При обеспечении перечисленных ранее условий, характеристики направленности и входное сопротивление полоскового вибратора можно определить по соотношениям для проволочного вибратора (см. параграф 1.1). Для этого нужно брать 2ρ=2d/2=d, что обеспечивает эквивалентность цилиндрического и плоского вибратора.
Возбуждение печатных вибраторов может осуществляться коаксиальной линией с симметрирующим устройством или симметричной полосковой линией. Часто используется питание несимметричной полосковой линией, что особенно удобно для «односторонних» вибраторов (рис. 1.9 б). При этом плечи вибратора должны иметь сдвиг по питанию на π (разность длин питающих линий λл/2) для обеспечения синфазности токов.
Щелевые полосковые антенны примеряются в том же частотном диапазоне и в тех же целях, что и волноводно-щелевые антенны. Главным их преимуществом является малая дисперсия полосковой линии передачи, а недостатком повышенные требования к ее коэффициенту затухания, особенно при большой длине антенной решетки.
Обычно щелевые излучатели прорезаются в одном из внешних проводников симметричной полосковой линии. Длина щели вычисляется по формуле:
, (1.21)где ε – относительная диэлектрическая проницаемость диэлектрика симметричной полосковой линии, λ – длина волны в свободном пространстве.
Расчетная длина щели уточняется экспериментально, так как на значение
оказывают влияние высшие типы волн в полосковой линии и поверхностные волны, которые возбуждаются щелью на много эффективнее чем полосковым вибратором.Для небольших решеток (число элементов N<10) используют или последовательное или параллельное питание щелей. Связь щели с полосковой линией регулируется смещением щели относительно проводника линии. Щель всегда перпендикулярна полосковой линии. В решетках большой длины щели возбуждаются бегущей волной тока. Возможно возбуждение и стоячей волной.
1.6 Рупорные антенны
В
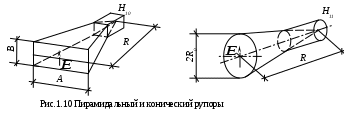сантиметровом и миллиметровом диапазонах волн широко применяются пирамидальные и конические рупорные антенны (рис.1.10).Пирамидальные рупоры возбуждаются прямоугольным волноводом, конические – круглым или, через плавный переход, прямоугольным. Если размер рупора В=b - ширине узкой стенки прямоугольного волновода, а размер А произвольный, рупор называется Н-секториальным (расширяется в плоскости вектора
). Если расширение делается только в плоскости вектора (А=а – широкой стенке волновода), то рупор Е-секториальный. При расширении в обеих плоскостях – пирамидальный рупор.Диаграмма направленности рупорной антенны определяется амплитудным и фазовым распределением поля в ее раскрыве. При небольших углах раскрыва рупора и при проведении оценочных расчетов ширины главного лепестка фазовыми искажениями можно пренебречь и воспользоваться данными табл. 3.1.
Размеры оптимального прямоугольного рупора связаны следующими соотношениями:
где
и - длина оптимального рупора соответственно в плоскостях векторов Е и Н. Если ≠ , то длина рупора R выбирается равной большему значению из них.Ширина главного лепестка диаграммы направленности оптимального прямоугольного рупора по уровню половинной мощности в плоскости вектора
определяется по эмпирической формуле: ,а в плоскости вектора